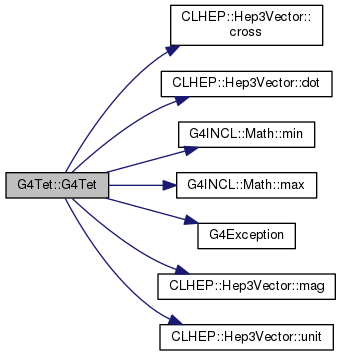
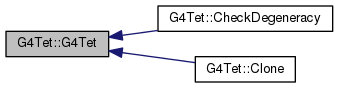
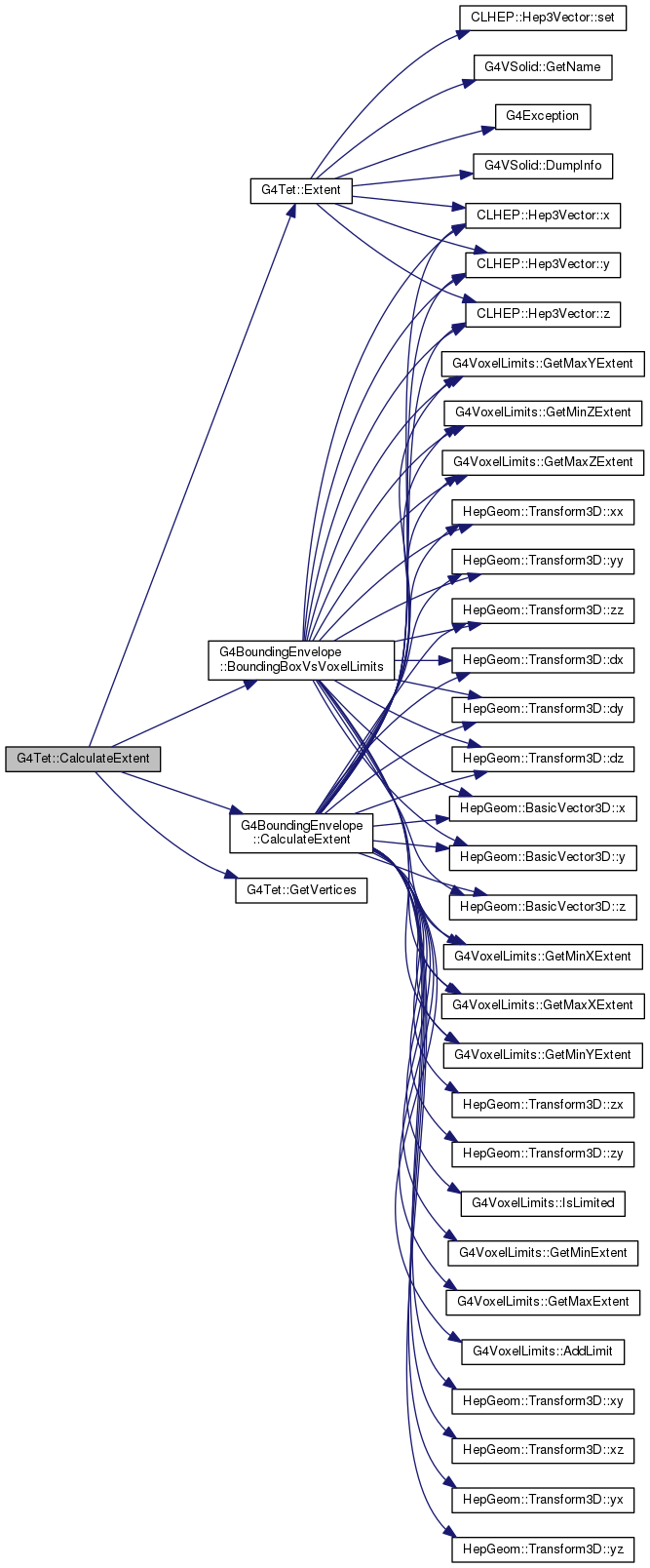
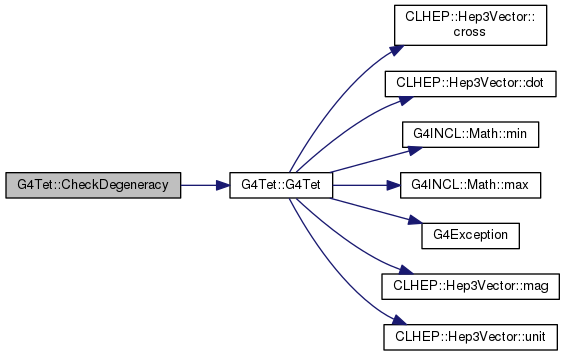
104 :
G4VSolid(pName), fRebuildPolyhedron(
false), fpPolyhedron(0), warningFlag(0)
124 fCubicVolume = std::fabs(signed_vol) / 6.;
137 fDx=(fXMax-fXMin)*0.5; fDy=(fYMax-fYMin)*0.5; fDz=(fZMax-fZMin)*0.5;
139 fMiddle=
G4ThreeVector(fXMax+fXMin, fYMax+fYMin, fZMax+fZMin)*0.5;
145 G4bool degenerate=std::fabs(signed_vol) < 1e-9*fMaxSize*fMaxSize*fMaxSize;
147 if(degeneracyFlag) *degeneracyFlag=degenerate;
151 "Degenerate tetrahedron not allowed.");
154 fTol=1e-9*(std::fabs(fXMin)+std::fabs(fXMax)+std::fabs(fYMin)
155 +std::fabs(fYMax)+std::fabs(fZMin)+std::fabs(fZMax));
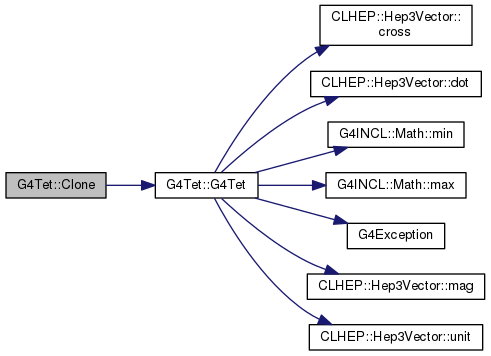
183 fNormal123=normal123.
unit();
184 fNormal134=normal134.
unit();
185 fNormal142=normal142.
unit();
186 fNormal234=normal234.
unit();
188 fCdotN123=fCenter123.
dot(fNormal123);
189 fCdotN134=fCenter134.
dot(fNormal134);
190 fCdotN142=fCenter142.
dot(fNormal142);
191 fCdotN234=fCenter234.
dot(fNormal234);
CLHEP::Hep3Vector G4ThreeVector
double dot(const Hep3Vector &) const
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
T max(const T t1, const T t2)
brief Return the largest of the two arguments
T min(const T t1, const T t2)
brief Return the smallest of the two arguments
G4VSolid(const G4String &name)
Hep3Vector cross(const Hep3Vector &) const
 Protected Member Functions inherited from G4VSolid
Protected Member Functions inherited from G4VSolid Protected Attributes inherited from G4VSolid
Protected Attributes inherited from G4VSolid