G4INCL::Math Namespace Reference

Functions
G4double	toDegrees (G4double radians)
G4int	heaviside (G4int n)
G4double	pow13 (G4double x)
G4double	powMinus13 (G4double x)
G4double	pow23 (G4double x)
G4double	aSinH (G4double x)
template<typename T >
G4int	sign (const T t)
template<typename T >
T	max (const T t1, const T t2)
	brief Return the largest of the two arguments More...
template<typename T >
T	min (const T t1, const T t2)
	brief Return the smallest of the two arguments More...
G4double	gaussianCDF (const G4double x)
	Cumulative distribution function for Gaussian. More...
G4double	gaussianCDF (const G4double x, const G4double x0, const G4double sigma)
	Generic cumulative distribution function for Gaussian. More...
G4double	inverseGaussianCDF (const G4double x)
	Inverse cumulative distribution function for Gaussian. More...
G4double	arcSin (const G4double x)
	Calculates arcsin with some tolerance on illegal arguments. More...
G4double	arcCos (const G4double x)
	Calculates arccos with some tolerance on illegal arguments. More...

Variables
const G4double	pi = 3.14159265358979323846264338328
const G4double	twoPi = 2.0 * pi
const G4double	tenPi = 10.0 * pi
const G4double	piOverTwo = 0.5 * pi
const G4double	oneOverSqrtTwo = 1./std::sqrt((G4double)2.)
const G4double	oneOverSqrtThree = 1./std::sqrt((G4double)3.)
const G4double	oneThird = 1./3.
const G4double	twoThirds = 2./3.
const G4double	sqrtFiveThirds = std::sqrt(5./3.)
const G4double	sqrtThreeFifths = std::sqrt(3./5.)

Function Documentation

G4double G4INCL::Math::arcCos

(

const G4double

x

)

Calculates arccos with some tolerance on illegal arguments.

Definition at line 103 of file G4INCLGlobals.cc.

                                      {
// assert(x>-1.000001 && x<1.000001);
      return ((x > 1.) ? 0. : ((x<-1.) ? pi : std::acos(x)));
    }

Here is the caller graph for this function:

G4double G4INCL::Math::arcSin

(

const G4double

x

)

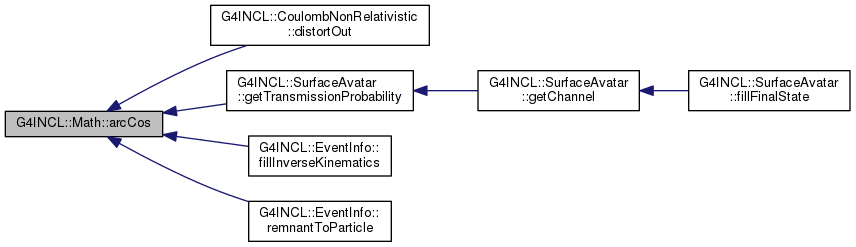
Calculates arcsin with some tolerance on illegal arguments.

Definition at line 98 of file G4INCLGlobals.cc.

                                      {
// assert(x>-1.000001 && x<1.000001);
      return ((x > 1.) ? 0. : ((x<-1.) ? pi : std::asin(x)));
    }

G4double G4INCL::Math::aSinH ( G4double  x )

inline

Definition at line 100 of file G4INCLGlobals.hh.

                                      {
      return std::log(x + std::sqrt(x*x+1.));
    }

G4double G4INCL::Math::gaussianCDF

(

const G4double

x

)

Cumulative distribution function for Gaussian.

A public-domain approximation taken from Abramowitz and Stegun. Applies to a Gaussian with mean=0 and sigma=1.

Parameters

x	a Gaussian variable

Definition at line 74 of file G4INCLGlobals.cc.

    {
      // Save the sign of x
      const G4double sgn = sign(x);
      const G4double z = std::fabs(x) * oneOverSqrtTwo;

      // A&S formula 7.1.26
      G4double t = 1.0/(1.0 + gcdfp*z);
      G4double y = 1.0 - (((((gcdfa5*t + gcdfa4)*t) + gcdfa3)*t + gcdfa2)*t + gcdfa1)*t*std::exp(-z*z);

      return 0.5*(1.0 + sgn*y);
    }

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4INCL::Math::gaussianCDF	(	const G4double	x,
		const G4double	x0,
		const G4double	sigma
	)

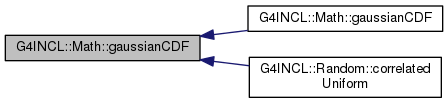
Generic cumulative distribution function for Gaussian.

A public-domain approximation taken from Abramowitz and Stegun. Applies to a generic Gaussian.

Parameters

x	a Gaussian variable
x0	mean of the Gaussian
sigma	standard deviation of the Gaussian

Definition at line 87 of file G4INCLGlobals.cc.

                                                                                    {
      return gaussianCDF((x-x0)/sigma);
    }

Here is the call graph for this function:

G4int G4INCL::Math::heaviside ( G4int  n )

inline

Definition at line 83 of file G4INCLGlobals.hh.

                                    {
      if(n < 0) return 0;
      else return 1;
    }

Here is the caller graph for this function:

G4double G4INCL::Math::inverseGaussianCDF

(

const G4double

x

)

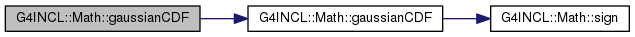
Inverse cumulative distribution function for Gaussian.

A public-domain approximation taken from Abramowitz and Stegun. Applies to a Gaussian with mean=0 and sigma=1.

Parameters

x	a uniform variate

Returns

a Gaussian variate

Definition at line 91 of file G4INCLGlobals.cc.

                                            {
      if (x < 0.5)
        return -inverseGaussianCDFRational( std::sqrt(-2.0*std::log(x)) );
      else
        return inverseGaussianCDFRational( std::sqrt(-2.0*std::log(1.-x)) );
    }

template<typename T >

T G4INCL::Math::max ( const T  t1, const T  t2  )

inline

brief Return the largest of the two arguments

Definition at line 112 of file G4INCLGlobals.hh.

                                                               {
      return t1 > t2 ? t1 : t2;
    }

template<typename T >

T G4INCL::Math::min ( const T  t1, const T  t2  )

inline

brief Return the smallest of the two arguments

Definition at line 117 of file G4INCLGlobals.hh.

                                                               {
      return t1 < t2 ? t1 : t2;
    }

G4double G4INCL::Math::pow13 ( G4double  x )

inline

Definition at line 88 of file G4INCLGlobals.hh.

                                      {
      return std::pow(x, oneThird);
    }

Here is the caller graph for this function:

G4double G4INCL::Math::pow23 ( G4double  x )

inline

Definition at line 96 of file G4INCLGlobals.hh.

                                      {
      return std::pow(x, twoThirds);
    }

G4double G4INCL::Math::powMinus13 ( G4double  x )

inline

Definition at line 92 of file G4INCLGlobals.hh.

                                           {
      return std::pow(x, -oneThird);
    }

template<typename T >

G4int G4INCL::Math::sign ( const T  t )

inline

A simple sign function that allows us to port fortran code to c++ more easily.

Definition at line 107 of file G4INCLGlobals.hh.

                                                       {
      return t > 0 ? 1: t < 0 ? -1 : 0;
    }

Here is the caller graph for this function:

G4double G4INCL::Math::toDegrees ( G4double  radians )

inline

Definition at line 79 of file G4INCLGlobals.hh.

                                                {
      return radians * (180.0 / pi);
    }

Here is the caller graph for this function:

Variable Documentation

const G4double G4INCL::Math::oneOverSqrtThree = 1./std::sqrt((G4double)3.)

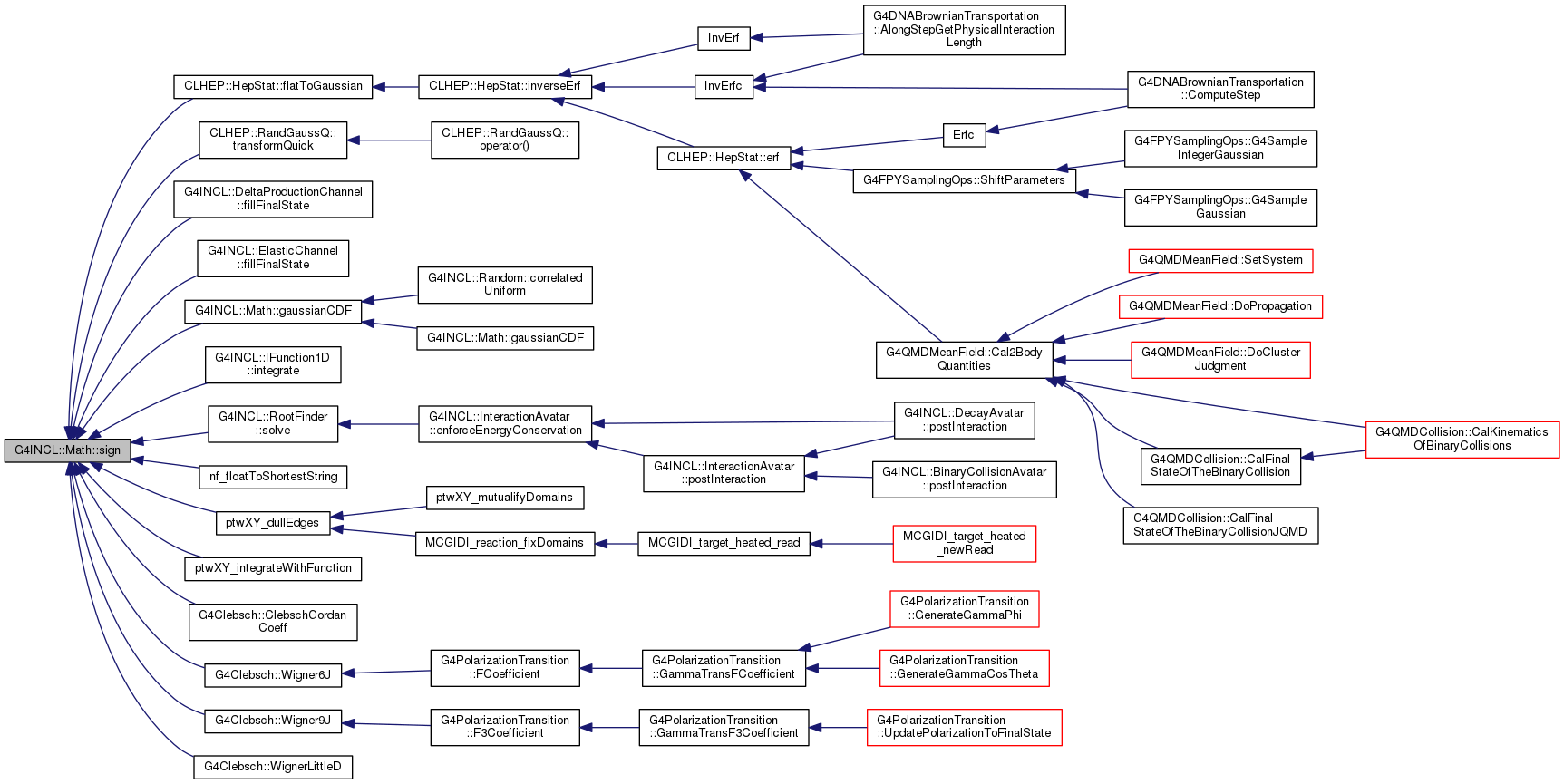
Definition at line 73 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::oneOverSqrtTwo = 1./std::sqrt((G4double)2.)

Definition at line 72 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::oneThird = 1./3.

Definition at line 74 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::pi = 3.14159265358979323846264338328

Definition at line 68 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::piOverTwo = 0.5 * pi

Definition at line 71 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::sqrtFiveThirds = std::sqrt(5./3.)

Definition at line 76 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::sqrtThreeFifths = std::sqrt(3./5.)

Definition at line 77 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::tenPi = 10.0 * pi

Definition at line 70 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::twoPi = 2.0 * pi

Definition at line 69 of file G4INCLGlobals.hh.

const G4double G4INCL::Math::twoThirds = 2./3.

Definition at line 75 of file G4INCLGlobals.hh.