G4HelixMixedStepper Class Reference

#include <G4HelixMixedStepper.hh>

Inheritance diagram for G4HelixMixedStepper:

Collaboration diagram for G4HelixMixedStepper:

Public Member Functions
	G4HelixMixedStepper (G4Mag_EqRhs *EqRhs, G4int StepperNumber=-1, G4double Angle_threshold=-1.0)
	~G4HelixMixedStepper ()
void	Stepper (const G4double y[], const G4double dydx[], G4double h, G4double yout[], G4double yerr[])
void	DumbStepper (const G4double y[], G4ThreeVector Bfld, G4double h, G4double yout[])
G4double	DistChord () const
void	SetVerbose (G4int newvalue)
void	PrintCalls ()
G4MagIntegratorStepper *	SetupStepper (G4Mag_EqRhs *EqRhs, G4int StepperName)
void	SetAngleThreshold (G4double val)
G4double	GetAngleThreshold ()
G4int	IntegratorOrder () const
Public Member Functions inherited from G4MagHelicalStepper
	G4MagHelicalStepper (G4Mag_EqRhs *EqRhs)
virtual	~G4MagHelicalStepper ()
G4double	DistChord () const
Public Member Functions inherited from G4MagIntegratorStepper
	G4MagIntegratorStepper (G4EquationOfMotion *Equation, G4int numIntegrationVariables, G4int numStateVariables=12, bool isFSAL=false)
virtual	~G4MagIntegratorStepper ()
virtual void	ComputeRightHandSide (const G4double y[], G4double dydx[])
void	NormaliseTangentVector (G4double vec[6])
void	NormalisePolarizationVector (G4double vec[12])
void	RightHandSide (const double y[], double dydx[])
G4int	GetNumberOfVariables () const
G4int	GetNumberOfStateVariables () const
G4int	IntegrationOrder ()
G4EquationOfMotion *	GetEquationOfMotion ()
void	SetEquationOfMotion (G4EquationOfMotion *newEquation)
unsigned long	GetfNoRHSCalls ()
void	ResetfNORHSCalls ()
bool	IsFSAL ()

Additional Inherited Members
Protected Member Functions inherited from G4MagHelicalStepper
void	LinearStep (const G4double yIn[], G4double h, G4double yHelix[]) const
void	AdvanceHelix (const G4double yIn[], G4ThreeVector Bfld, G4double h, G4double yHelix[], G4double yHelix2[]=0)
void	MagFieldEvaluate (const G4double y[], G4ThreeVector &Bfield)
G4double	GetInverseCurve (const G4double Momentum, const G4double Bmag)
void	SetAngCurve (const G4double Ang)
G4double	GetAngCurve () const
void	SetCurve (const G4double Curve)
G4double	GetCurve () const
void	SetRadHelix (const G4double Rad)
G4double	GetRadHelix () const
Protected Member Functions inherited from G4MagIntegratorStepper
void	SetIntegrationOrder (int order)
void	SetFSAL (bool flag=true)

Detailed Description

Definition at line 66 of file G4HelixMixedStepper.hh.

Constructor & Destructor Documentation

G4HelixMixedStepper::G4HelixMixedStepper	(	G4Mag_EqRhs *	EqRhs,
		G4int	StepperNumber = -1,
		G4double	Angle_threshold = -1.0
	)

Definition at line 65 of file G4HelixMixedStepper.cc.

  : G4MagHelicalStepper(EqRhs), fNumCallsRK4(0), fNumCallsHelix(0)
{
   SetVerbose(1);
   if( angleThreshold < 0.0 ){
     fAngle_threshold= 0.33*pi;
   }else{
     fAngle_threshold= angleThreshold;
   }

   if(stepperNumber<0)
     stepperNumber=4;  // Default is RK4   (original)      
     // stepperNumber=745;   // Default is DormandPrince745 (ie DoPri5)
     // stepperNumber=8;  // Default is CashKarp

   fStepperNumber = stepperNumber; // Store the choice
   fRK4Stepper =  SetupStepper(EqRhs, fStepperNumber);
}

Here is the call graph for this function:

G4HelixMixedStepper::~G4HelixMixedStepper

(

)

Definition at line 85 of file G4HelixMixedStepper.cc.

{  
  delete(fRK4Stepper);
  if (fVerbose>0){ PrintCalls();};
}

Here is the call graph for this function:

Member Function Documentation

G4double G4HelixMixedStepper::DistChord ( ) const

virtual

Implements G4MagIntegratorStepper.

Definition at line 160 of file G4HelixMixedStepper.cc.

{
  // Implementation : must check whether h/R > 2 pi  !!
  //   If( h/R <  pi) use G4LineSection::DistLine
  //   Else           DistChord=R_helix
  //
  G4double distChord;
  G4double Ang_curve=GetAngCurve();
  
  if(Ang_curve<=pi){
    distChord=GetRadHelix()*(1-std::cos(0.5*Ang_curve));
  }
  else
  {
    if(Ang_curve<twopi){
      distChord=GetRadHelix()*(1+std::cos(0.5*(twopi-Ang_curve)));
    }
    else{
      distChord=2.*GetRadHelix();
    }
  }
  
  return distChord;
}

Here is the call graph for this function:

void G4HelixMixedStepper::DumbStepper ( const G4double  y[], G4ThreeVector  Bfld, G4double  h, G4double  yout[]  )

virtual

Implements G4MagHelicalStepper.

Definition at line 152 of file G4HelixMixedStepper.cc.

{
  AdvanceHelix(yIn, Bfld, h, yOut);
}

Here is the call graph for this function:

G4double G4HelixMixedStepper::GetAngleThreshold ( )

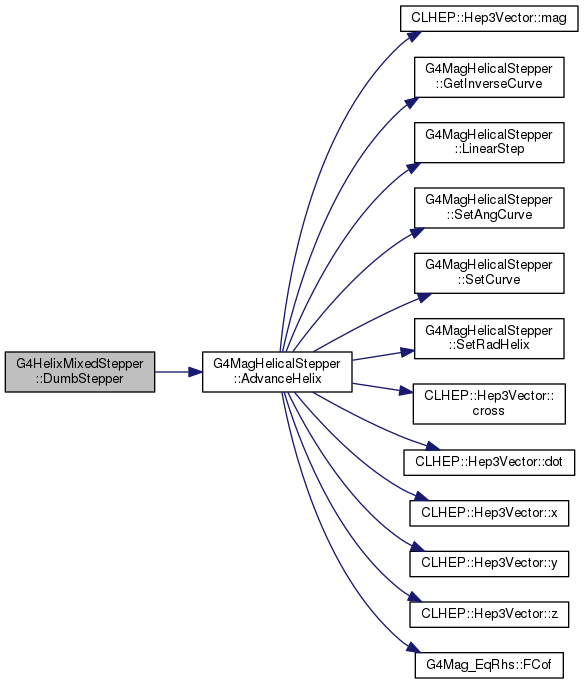
inline

Definition at line 101 of file G4HelixMixedStepper.hh.

{ return fAngle_threshold; }

G4int G4HelixMixedStepper::IntegratorOrder ( ) const

inlinevirtual

Implements G4MagIntegratorStepper.

Definition at line 103 of file G4HelixMixedStepper.hh.

{ return 4; }

void G4HelixMixedStepper::PrintCalls

(

)

Definition at line 186 of file G4HelixMixedStepper.cc.

{
  G4cout << "In HelixMixedStepper::Number of calls to smallStepStepper = "
         << fNumCallsRK4
         << "  and Number of calls to Helix = " << fNumCallsHelix << G4endl;
}

Here is the caller graph for this function:

void G4HelixMixedStepper::SetAngleThreshold ( G4double  val )

inline

Definition at line 100 of file G4HelixMixedStepper.hh.

{ fAngle_threshold= val;}

G4MagIntegratorStepper * G4HelixMixedStepper::SetupStepper	(	G4Mag_EqRhs *	EqRhs,
		G4int	StepperName
	)

Definition at line 194 of file G4HelixMixedStepper.cc.

{
  G4MagIntegratorStepper* pStepper;
  if (fVerbose>0) G4cout << " G4HelixMixedStepper: ";
  switch ( StepperNumber )
    {
      // Robust, classic method
      case 4:
        pStepper = new G4ClassicalRK4( pE );
        if (fVerbose>0) G4cout << "G4ClassicalRK4";
        break;

      // Steppers with embedded estimation of error
      case 8:
        pStepper = new G4CashKarpRKF45( pE );
        if (fVerbose>0) G4cout << "G4CashKarpRKF45";
        break;
      case 13:
        pStepper = new G4NystromRK4( pE );
        if (fVerbose>0) G4cout << "G4NystromRK4";
        break;
        
      // Lowest order RK Stepper - experimental
      case 1:
        pStepper = new G4ImplicitEuler( pE );
        if (fVerbose>0) G4cout << "G4ImplicitEuler";
        break;

      // Lower order RK Steppers - ok overall, good for uneven fields        
      case 2:
        pStepper = new G4SimpleRunge( pE );
        if (fVerbose>0) G4cout << "G4SimpleRunge";
        break;
      case 3:
        pStepper = new G4SimpleHeum( pE );
        if (fVerbose>0) G4cout << "G4SimpleHeum";
        break;
      case 23:
        pStepper = new G4BogackiShampine23( pE );
        if (fVerbose>0) G4cout << "G4BogackiShampine23";
        break;

      // Higher order RK Steppers
      // for smoother fields and high accuracy requirements 
      case 45:
        pStepper = new G4BogackiShampine45( pE );
        if (fVerbose>0) G4cout << "G4BogackiShampine45";
        break;
      case 145:
        pStepper = new G4TsitourasRK45( pE );
        if (fVerbose>0) G4cout << "G4TsitourasRK45";
        break;
      case 745:
        pStepper = new G4DormandPrince745( pE );
        if (fVerbose>0) G4cout << "G4DormandPrince745";
        break;

      // Helical Steppers
      case 6:
        pStepper = new G4HelixImplicitEuler( pE );
        if (fVerbose>0) G4cout << "G4HelixImplicitEuler";
        break;
      case 7:
        pStepper = new G4HelixSimpleRunge( pE );
        if (fVerbose>0) G4cout << "G4HelixSimpleRunge";
        break;
      case 5:
        pStepper = new G4HelixExplicitEuler( pE );
        if (fVerbose>0) G4cout << "G4HelixExplicitEuler";
        break; //  Since Helix Explicit is used for long steps,
               // this is useful only to measure overhead.
      // Exact Helix - likely good only for cases of
      //            i) uniform field (potentially over small distances)
      //           ii) segmented uniform field (maybe)
      case 9:
        pStepper = new G4ExactHelixStepper( pE );
        if (fVerbose>0) G4cout << "G4ExactHelixStepper";
        break;
      case 10:
        pStepper = new G4RKG3_Stepper( pE );
        if (fVerbose>0) G4cout << "G4RKG3_Stepper";
        break;

      // Low Order Steppers - not good except for very weak fields
      case 11:
        pStepper = new G4ExplicitEuler( pE );
        if (fVerbose>0) G4cout << "G4ExplicitEuler";
        break;
      case 12:
        pStepper = new G4ImplicitEuler( pE );
        if (fVerbose>0) G4cout << "G4ImplicitEuler";
        break;

      case 0:
      case -1:
      default:
        pStepper = new G4ClassicalRK4( pE );
        if (fVerbose>0) G4cout << "G4ClassicalRK4 (Default)";
        break;
    }
  if(fVerbose>0)
    G4cout << " chosen as stepper for small steps in G4HelixMixedStepper."
           << G4endl;

  return pStepper;
}

Here is the caller graph for this function:

void G4HelixMixedStepper::SetVerbose ( G4int  newvalue )

inline

Definition at line 94 of file G4HelixMixedStepper.hh.

{fVerbose=newvalue;}

Here is the caller graph for this function:

void G4HelixMixedStepper::Stepper ( const G4double  y[], const G4double  dydx[], G4double  h, G4double  yout[], G4double  yerr[]  )

virtual

Reimplemented from G4MagHelicalStepper.

Definition at line 91 of file G4HelixMixedStepper.cc.

{
  //Estimation of the Stepping Angle
  G4ThreeVector Bfld;
  MagFieldEvaluate(yInput, Bfld);
  
  G4double Bmag = Bfld.mag();
  const G4double *pIn = yInput+3;
  G4ThreeVector initVelocity= G4ThreeVector( pIn[0], pIn[1], pIn[2]);
  G4double      velocityVal = initVelocity.mag();
  G4double R_1;
  G4double Ang_curve;
  
  R_1=std::abs(GetInverseCurve(velocityVal,Bmag));
  Ang_curve=R_1*Step;
  SetAngCurve(Ang_curve);
  SetCurve(std::abs(1/R_1));
  
  if(Ang_curve< fAngle_threshold){
    fNumCallsRK4++;
    fRK4Stepper->Stepper(yInput,dydx,Step,yOut,yErr);
  }
  else
  {
    fNumCallsHelix++;
    const G4int    nvar    = 6 ;
    const G4int    nvarMax = 8 ;    
    G4int          i;
    G4double       yTemp[nvarMax], yIn[nvarMax], yTemp2[nvarMax];
    G4ThreeVector  Bfld_midpoint;

    //  Saving yInput because yInput and yOut can be aliases for same array
    for(i=0;i<nvar;i++) yIn[i]=yInput[i];
    
    G4double halfS = Step * 0.5;
    // 1. Do first half step and full step
    AdvanceHelix(yIn, Bfld, halfS, yTemp, yTemp2); // yTemp2 for s=2*h (halfS)
    //**********

    MagFieldEvaluate(yTemp, Bfld_midpoint) ;

    // 2. Do second half step - with revised field
    // NOTE: Could avoid this call if  'Bfld_midpoint == Bfld'
    //       or diff 'almost' zero
    AdvanceHelix(yTemp, Bfld_midpoint, halfS, yOut);
    // Not requesting y at s=2*h (halfS)
    //**********
    
    // 3. Estimate the integration error
    //    should be (nearly) zero if Bfield= constant
    for(i=0;i<nvar;i++) {
      yErr[i] = yOut[i] - yTemp2[i] ;
    }
  }
}

Here is the call graph for this function:

---

The documentation for this class was generated from the following files:

• source/geant4.10.03.p03/source/geometry/magneticfield/include/G4HelixMixedStepper.hh
• source/geant4.10.03.p03/source/geometry/magneticfield/src/G4HelixMixedStepper.cc