|
Geant4
10.03.p03
|
|
Geant4
10.03.p03
|
#include <Transform3D.h>

Classes | |
| class | Transform3D_row |
Public Member Functions | |
| Transform3D () | |
| Transform3D (const CLHEP::HepRotation &m, const CLHEP::Hep3Vector &v) | |
| Transform3D (const Point3D< double > &fr0, const Point3D< double > &fr1, const Point3D< double > &fr2, const Point3D< double > &to0, const Point3D< double > &to1, const Point3D< double > &to2) | |
| Transform3D (const Transform3D &m) | |
| ~Transform3D () | |
| const Transform3D_row | operator[] (int) const |
| double | operator() (int, int) const |
| double | xx () const |
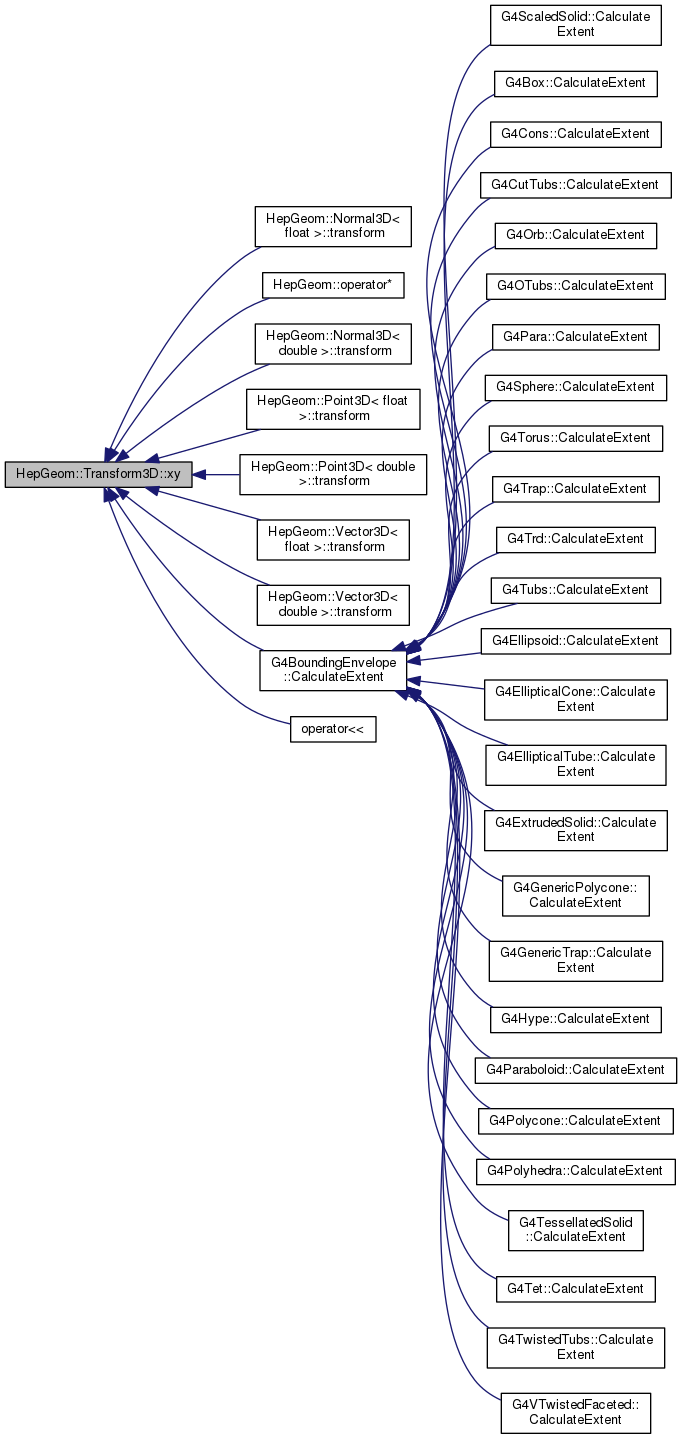
| double | xy () const |
| double | xz () const |
| double | yx () const |
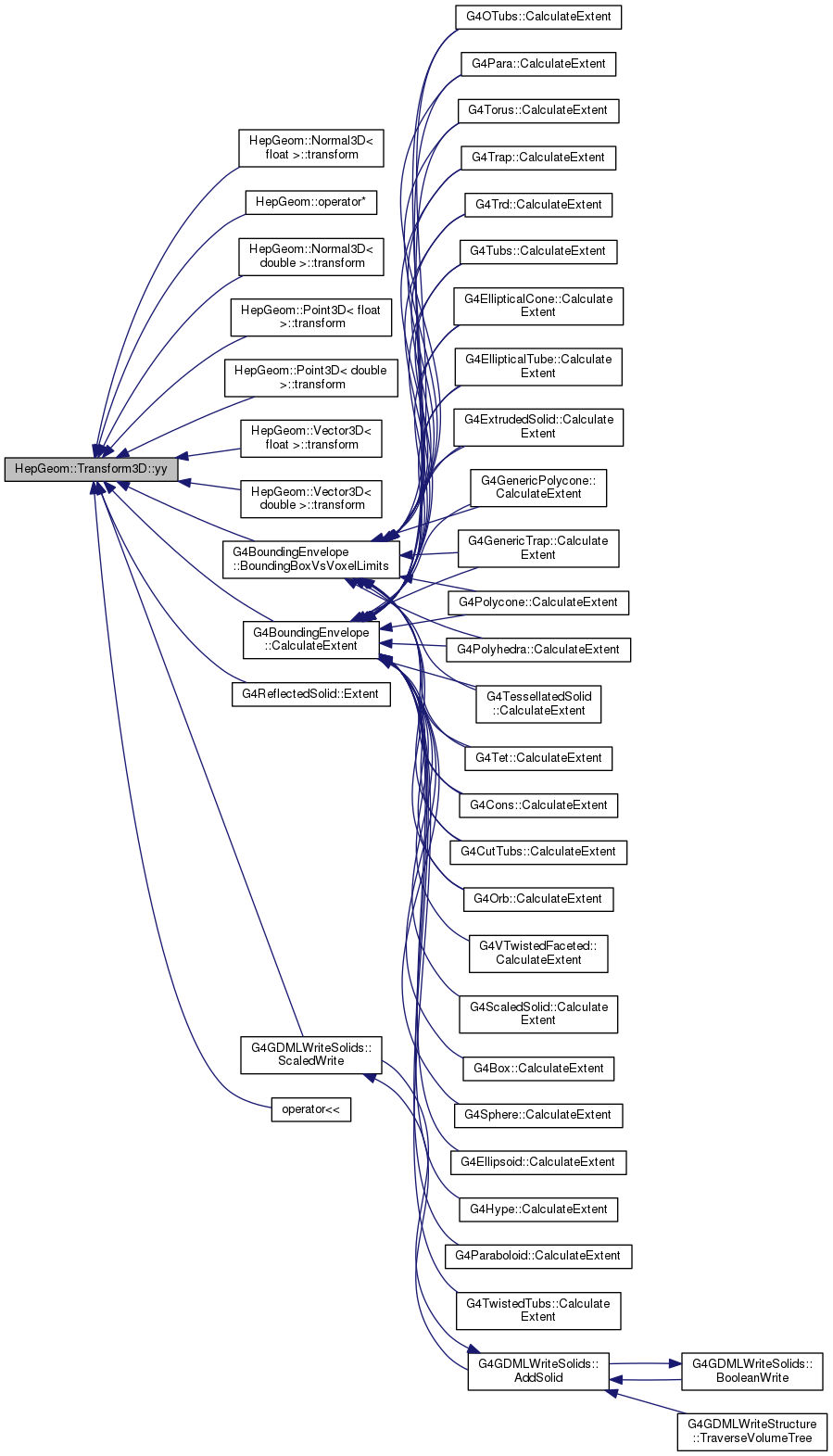
| double | yy () const |
| double | yz () const |
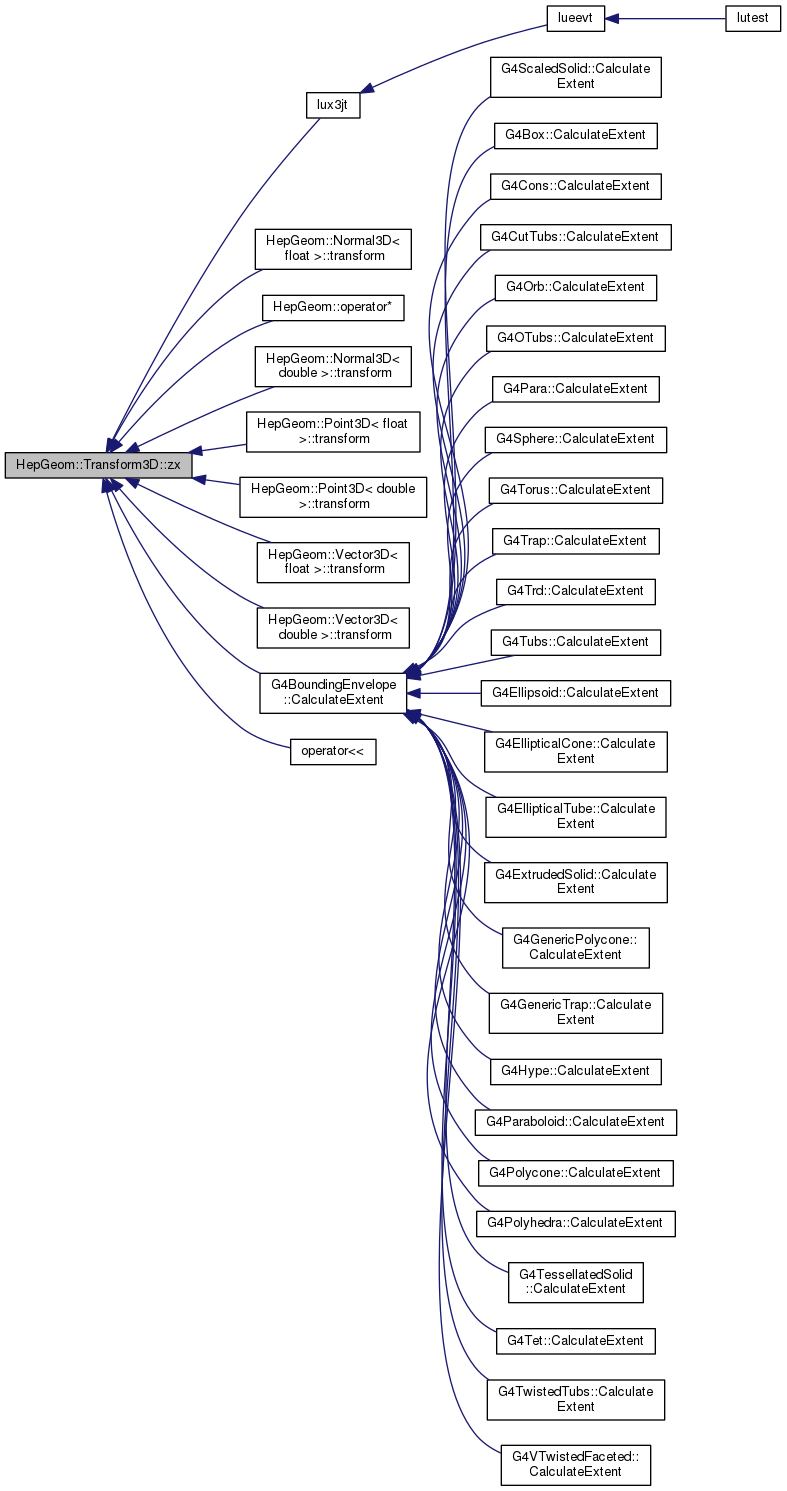
| double | zx () const |
| double | zy () const |
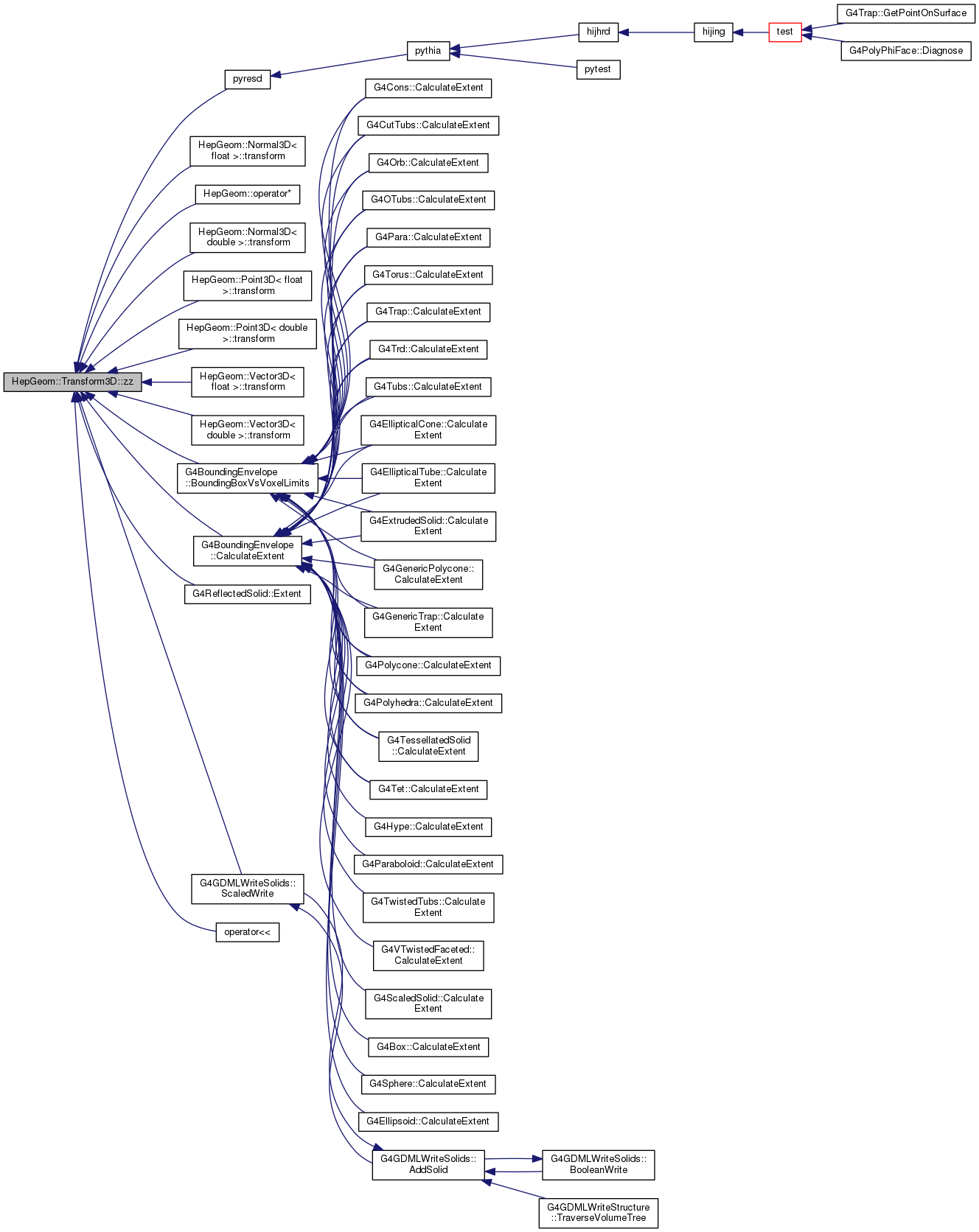
| double | zz () const |
| double | dx () const |
| double | dy () const |
| double | dz () const |
| Transform3D & | operator= (const Transform3D &m) |
| void | setIdentity () |
| Transform3D | inverse () const |
| Transform3D | operator* (const Transform3D &b) const |
| void | getDecomposition (Scale3D &scale, Rotate3D &rotation, Translate3D &translation) const |
| bool | isNear (const Transform3D &t, double tolerance=2.2E-14) const |
| CLHEP::HepRotation | getRotation () const |
| CLHEP::Hep3Vector | getTranslation () const |
| bool | operator== (const Transform3D &transform) const |
| bool | operator!= (const Transform3D &transform) const |
Static Public Attributes | |
| static const Transform3D | Identity = Transform3D () |
Protected Member Functions | |
| Transform3D (double XX, double XY, double XZ, double DX, double YX, double YY, double YZ, double DY, double ZX, double ZY, double ZZ, double DZ) | |
| void | setTransform (double XX, double XY, double XZ, double DX, double YX, double YY, double YZ, double DY, double ZX, double ZY, double ZZ, double DZ) |
Protected Attributes | |
| double | xx_ |
| double | xy_ |
| double | xz_ |
| double | dx_ |
| double | yx_ |
| double | yy_ |
| double | yz_ |
| double | dy_ |
| double | zx_ |
| double | zy_ |
| double | zz_ |
| double | dz_ |
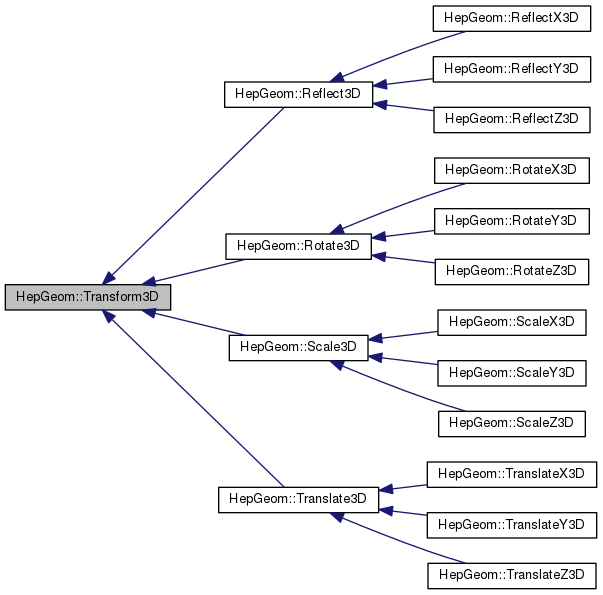
Class for transformation of 3D geometrical objects. It allows different translations, rotations, scalings and reflections. Several specialized classes are derived from it:
TranslateX3D, TranslateY3D, TranslateZ3D, Translate3D,
RotateX3D, RotateY3D, RotateZ3D, Rotate3D,
ScaleX3D, ScaleY3D, ScaleZ3D, Scale3D,
ReflectX3D, ReflectY3D, ReflectZ3D, Reflect3D.
The idea behind these classes is to provide some additional constructors for Transform3D, they normally should not be used as separate classes.
Example:
Remark: For the reason that the operator* is left associative, the notation
is much more effective then the notation
In the first case three operations Transform3D*Vector3D are executed, in the second case two operations Transform3D*Transform3D and one Transform3D*Vector3D are performed. Transform3D*Transform3D is roughly three times slower than Transform3D*Vector3D.
Definition at line 171 of file Transform3D.h.
|
inlineprotected |
Definition at line 178 of file Transform3D.h.
|
inline |
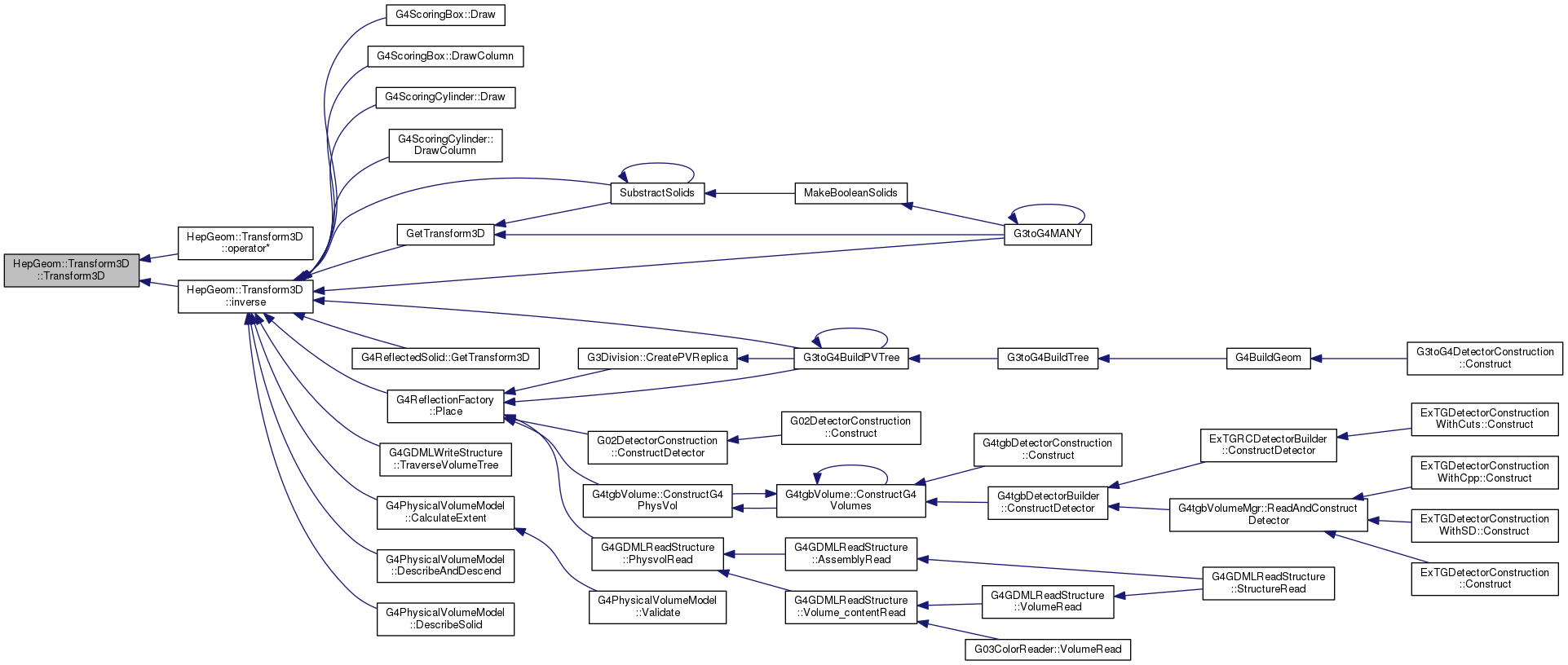
Default constructor - sets the Identity transformation.
Definition at line 211 of file Transform3D.h.
|
inline |
Constructor: rotation and then translation.
| HepGeom::Transform3D::Transform3D | ( | const Point3D< double > & | fr0, |
| const Point3D< double > & | fr1, | ||
| const Point3D< double > & | fr2, | ||
| const Point3D< double > & | to0, | ||
| const Point3D< double > & | to1, | ||
| const Point3D< double > & | to2 | ||
| ) |
Constructor: transformation of basis (assumed - no reflection).
Definition at line 63 of file Transform3D.cc.

|
inline |
|
inline |
Destructor. Virtual for now as some persistency mechanism needs that, in future releases this might go away again.
Definition at line 241 of file Transform3D.h.
|
inline |
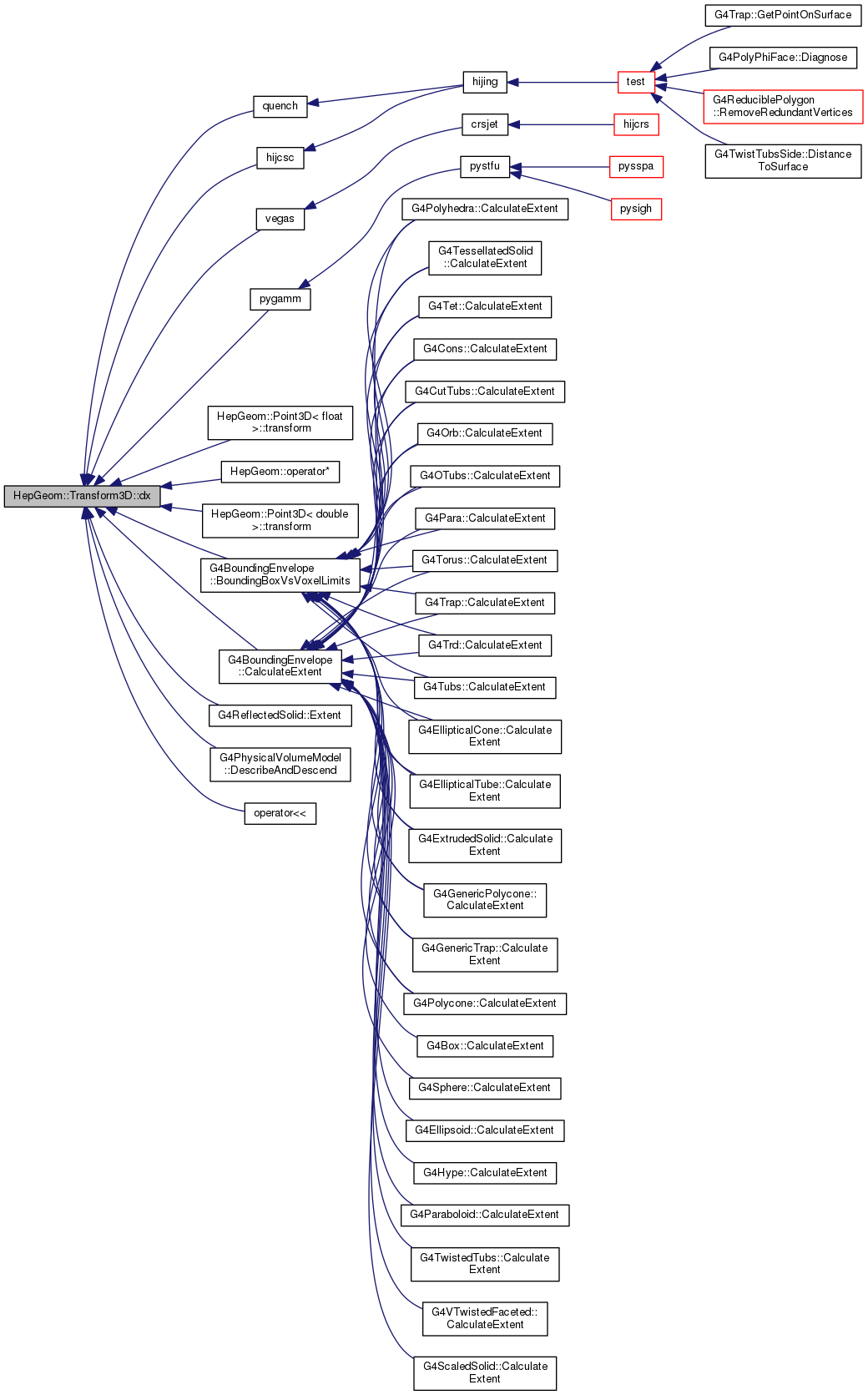
Gets dx-element of the transformation matrix.
Definition at line 279 of file Transform3D.h.
|
inline |
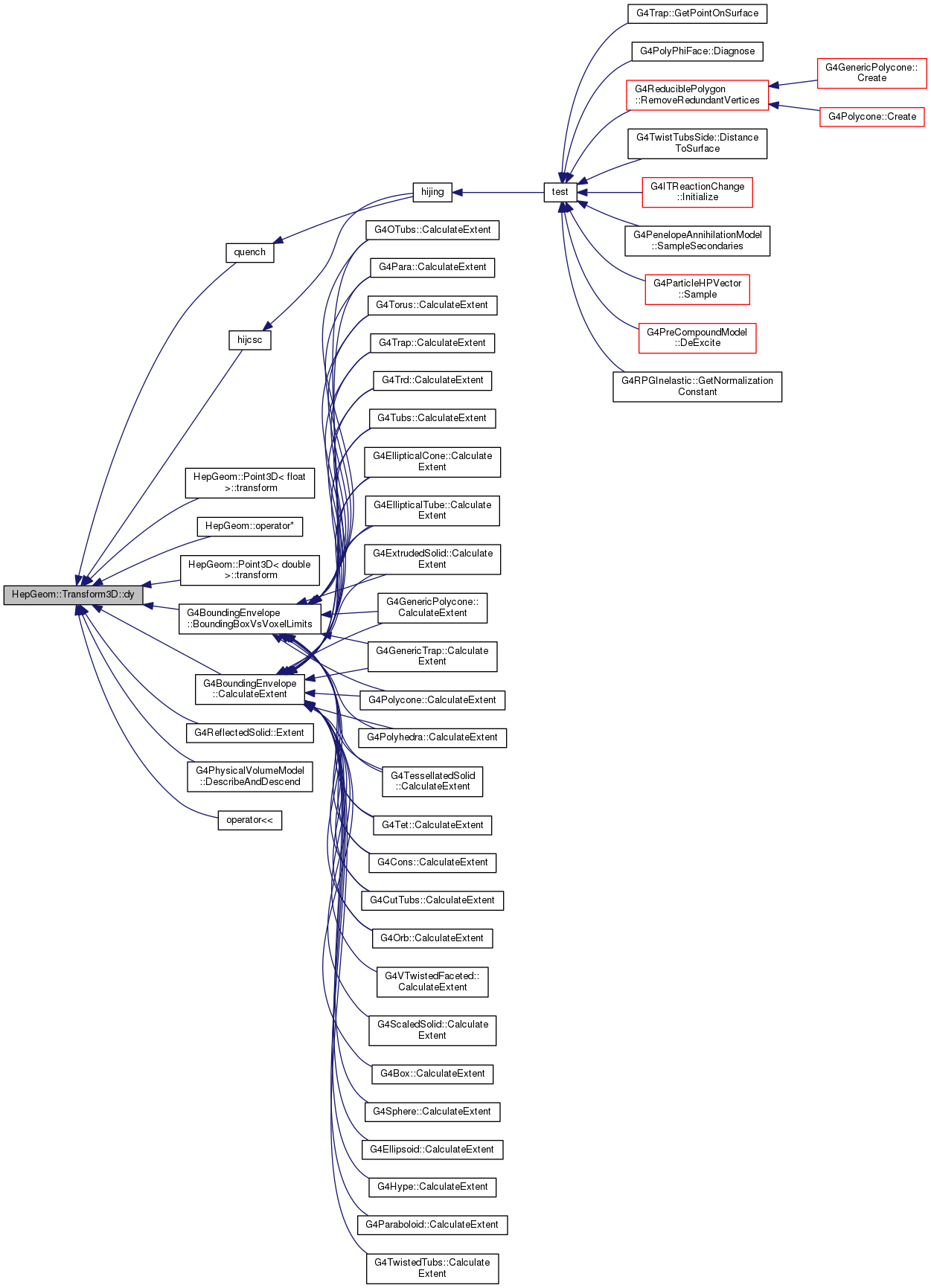
Gets dy-element of the transformation matrix.
Definition at line 282 of file Transform3D.h.
|
inline |
Gets dz-element of the transformation matrix.
Definition at line 285 of file Transform3D.h.

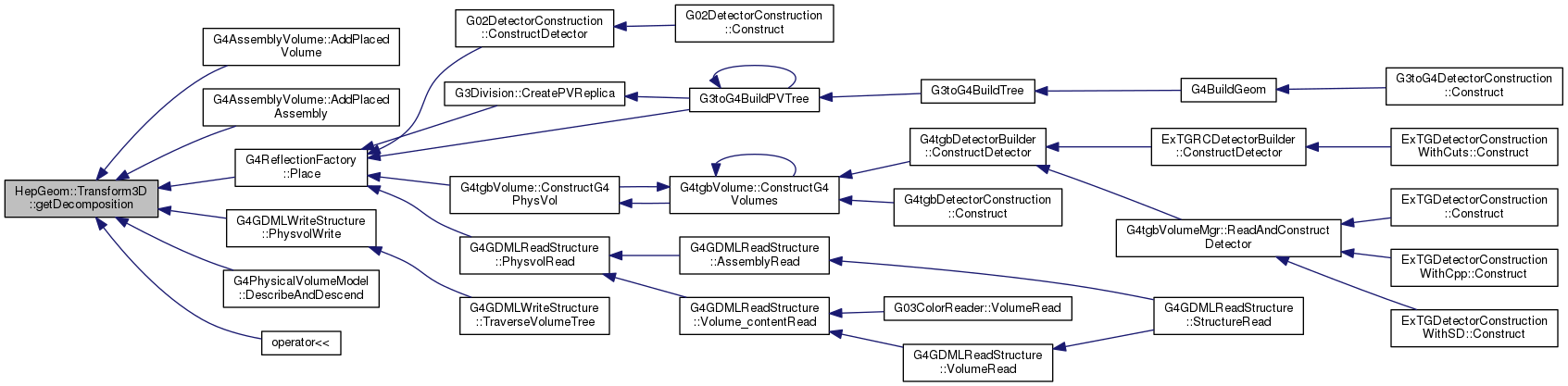
| void HepGeom::Transform3D::getDecomposition | ( | Scale3D & | scale, |
| Rotate3D & | rotation, | ||
| Translate3D & | translation | ||
| ) | const |
Decomposition of general transformation. This function gets decomposition of the transformation in three consequentive specific transformations: Scale3D, then Rotate3D, then Translate3, i.e.
| scale | output: scaling transformation; if there was a reflection, then scale factor for z-component (scale(2,2)) will be negative. |
| rotation | output: rotation transformaion. |
| translation | output: translation transformaion. |
Definition at line 174 of file Transform3D.cc.
|
inline |
Extracts the rotation matrix. This functions is obsolete - use getDecomposition() instead.

|
inline |
Extracts the translation vector. This functions is obsolete - use getDecomposition() instead.
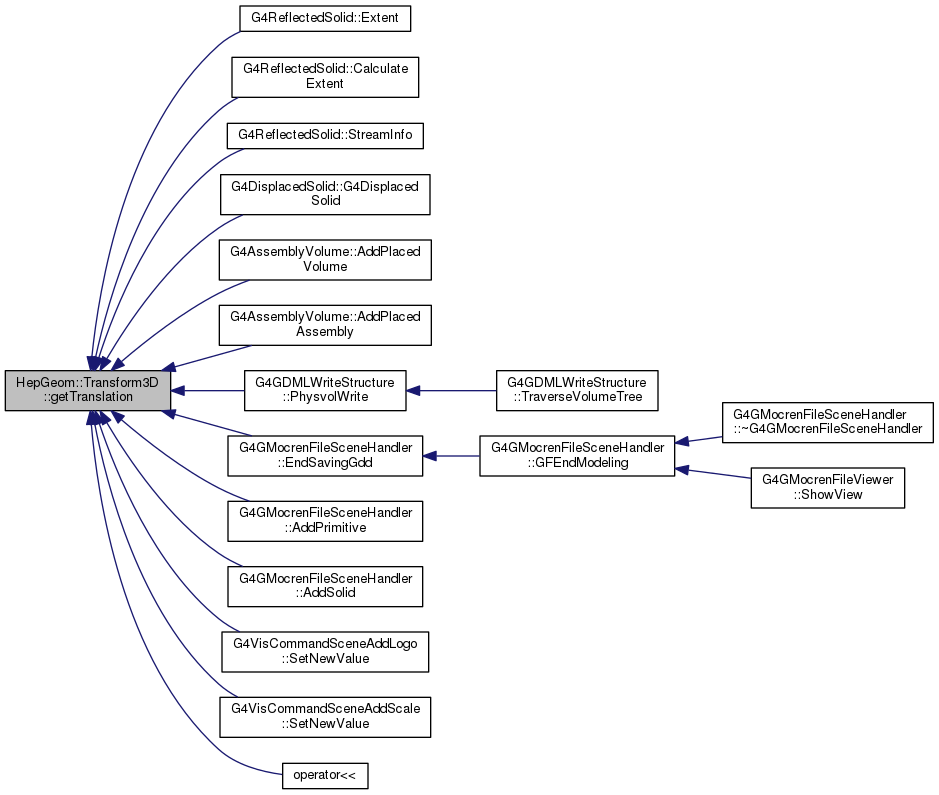
| Transform3D HepGeom::Transform3D::inverse | ( | ) | const |
Returns the inverse transformation.
Definition at line 142 of file Transform3D.cc.


| bool HepGeom::Transform3D::isNear | ( | const Transform3D & | t, |
| double | tolerance = 2.2E-14 |
||
| ) | const |
Returns true if the difference between corresponding matrix elements is less than the tolerance.
Definition at line 204 of file Transform3D.cc.
|
inline |
Test for inequality.
Definition at line 353 of file Transform3D.h.

Fortran-style subscripting: returns (i,j) element of the matrix.
Definition at line 24 of file Transform3D.cc.
| Transform3D HepGeom::Transform3D::operator* | ( | const Transform3D & | b | ) | const |
Transformation by another Transform3D.
Definition at line 52 of file Transform3D.cc.

|
inline |
| bool HepGeom::Transform3D::operator== | ( | const Transform3D & | transform | ) | const |
Test for equality.
Definition at line 221 of file Transform3D.cc.

|
inline |
Returns object of the helper class for C-style subscripting r[i][j]
|
inline |
Sets the Identity transformation.
Definition at line 298 of file Transform3D.h.
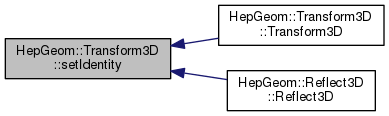
|
inlineprotected |
|
inline |
Gets xx-element of the transformation matrix.
Definition at line 252 of file Transform3D.h.
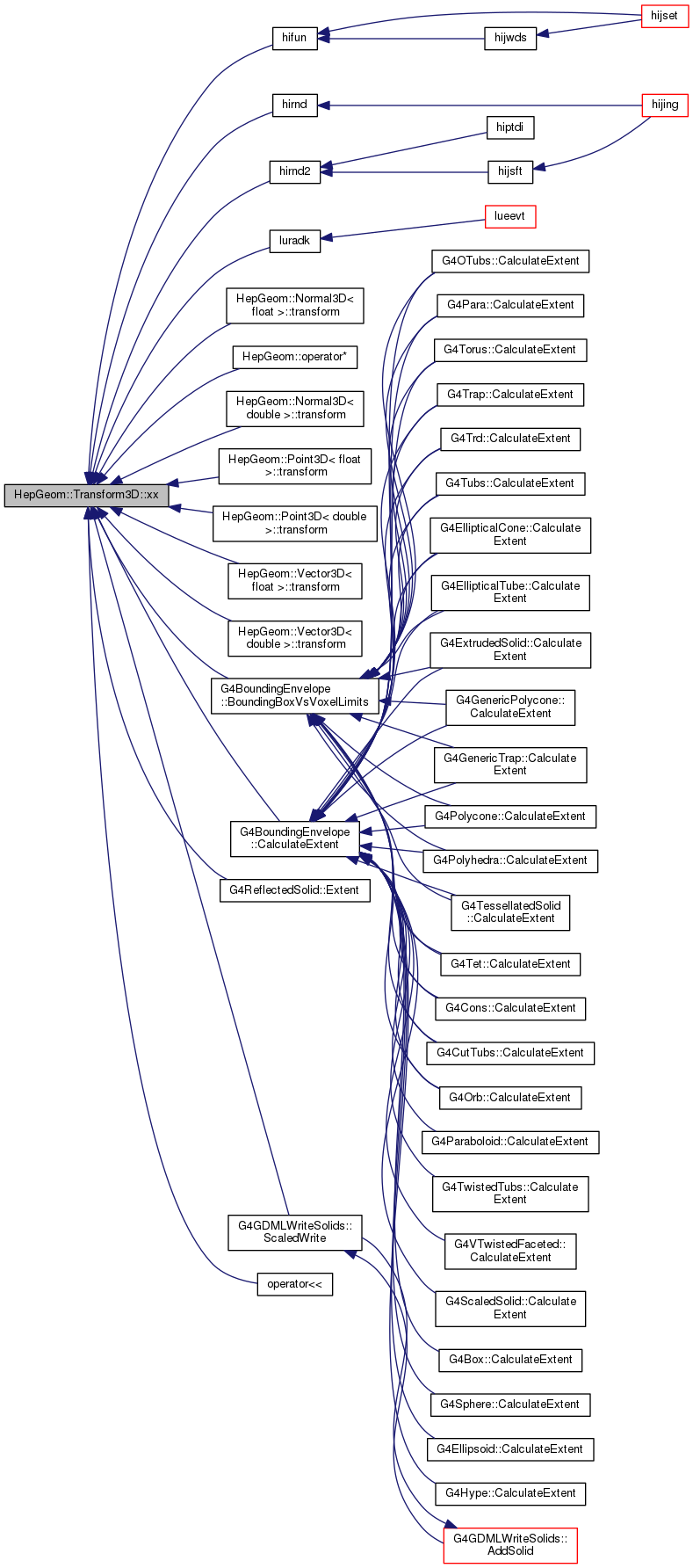
|
inline |
Gets xy-element of the transformation matrix.
Definition at line 255 of file Transform3D.h.
|
inline |
Gets xz-element of the transformation matrix.
Definition at line 258 of file Transform3D.h.

|
inline |
Gets yx-element of the transformation matrix.
Definition at line 261 of file Transform3D.h.

|
inline |
Gets yy-element of the transformation matrix.
Definition at line 264 of file Transform3D.h.
|
inline |
Gets yz-element of the transformation matrix.
Definition at line 267 of file Transform3D.h.

|
inline |
Gets zx-element of the transformation matrix.
Definition at line 270 of file Transform3D.h.
|
inline |
Gets zy-element of the transformation matrix.
Definition at line 273 of file Transform3D.h.

|
inline |
Gets zz-element of the transformation matrix.
Definition at line 276 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
static |
Global identity transformation.
Definition at line 197 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.
|
protected |
Definition at line 173 of file Transform3D.h.