|
| | HepRotation () |
| |
| | HepRotation (const HepRotation &m) |
| |
| | HepRotation (const HepRotationX &m) |
| |
| | HepRotation (const HepRotationY &m) |
| |
| | HepRotation (const HepRotationZ &m) |
| |
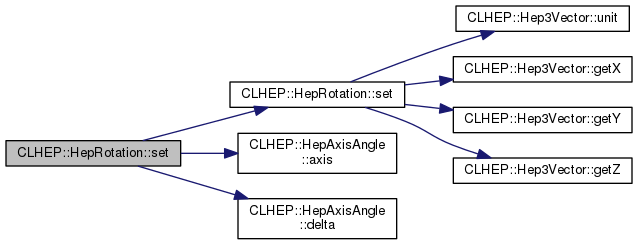
| HepRotation & | set (const Hep3Vector &axis, double delta) |
| |
| | HepRotation (const Hep3Vector &axis, double delta) |
| |
| HepRotation & | set (const HepAxisAngle &ax) |
| |
| | HepRotation (const HepAxisAngle &ax) |
| |
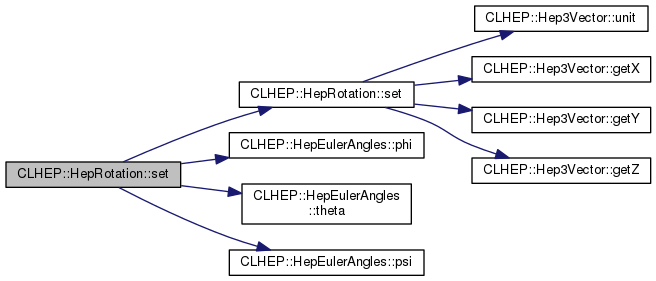
| HepRotation & | set (double phi, double theta, double psi) |
| |
| | HepRotation (double phi, double theta, double psi) |
| |
| HepRotation & | set (const HepEulerAngles &e) |
| |
| | HepRotation (const HepEulerAngles &e) |
| |
| | HepRotation (const Hep3Vector &colX, const Hep3Vector &colY, const Hep3Vector &colZ) |
| |
| HepRotation & | set (const Hep3Vector &colX, const Hep3Vector &colY, const Hep3Vector &colZ) |
| |
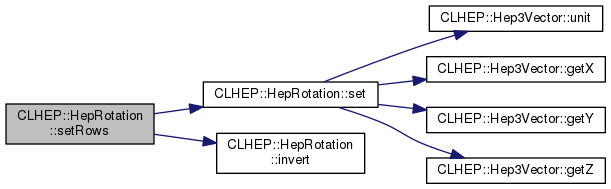
| HepRotation & | setRows (const Hep3Vector &rowX, const Hep3Vector &rowY, const Hep3Vector &rowZ) |
| |
| HepRotation & | set (const HepRotationX &r) |
| |
| HepRotation & | set (const HepRotationY &r) |
| |
| HepRotation & | set (const HepRotationZ &r) |
| |
| HepRotation & | operator= (const HepRotation &r) |
| |
| HepRotation & | operator= (const HepRotationX &r) |
| |
| HepRotation & | operator= (const HepRotationY &r) |
| |
| HepRotation & | operator= (const HepRotationZ &r) |
| |
| HepRotation & | set (const HepRep3x3 &m) |
| |
| | HepRotation (const HepRep3x3 &m) |
| |
| | ~HepRotation () |
| |
| Hep3Vector | colX () const |
| |
| Hep3Vector | colY () const |
| |
| Hep3Vector | colZ () const |
| |
| Hep3Vector | rowX () const |
| |
| Hep3Vector | rowY () const |
| |
| Hep3Vector | rowZ () const |
| |
| double | xx () const |
| |
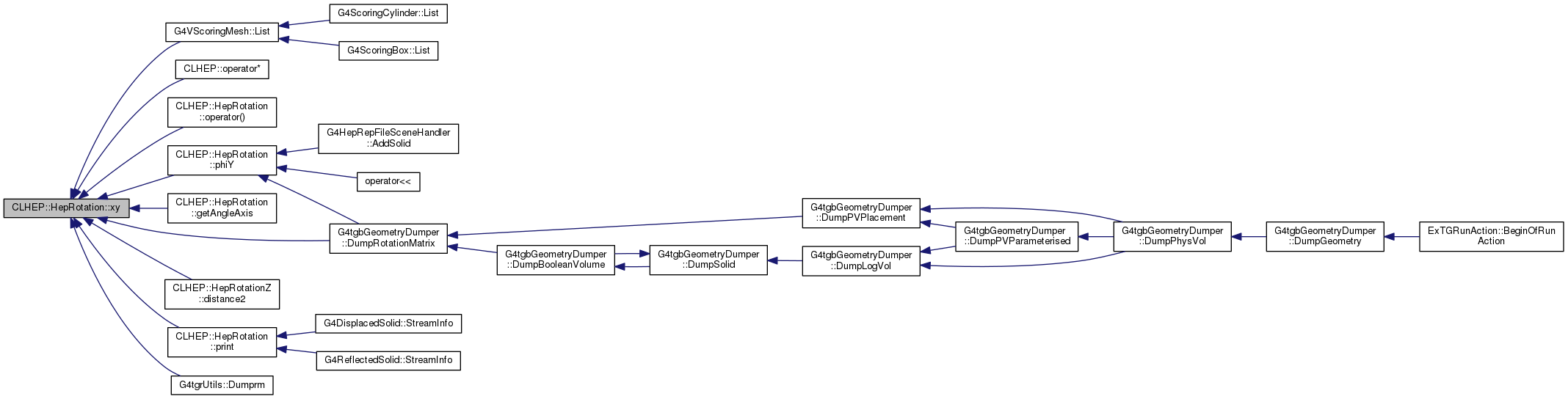
| double | xy () const |
| |
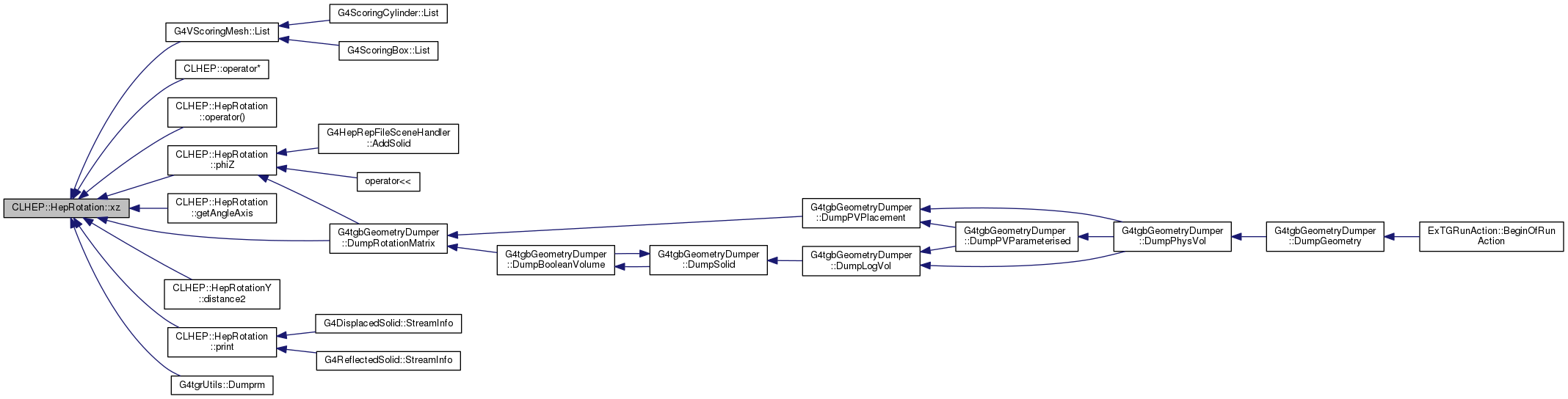
| double | xz () const |
| |
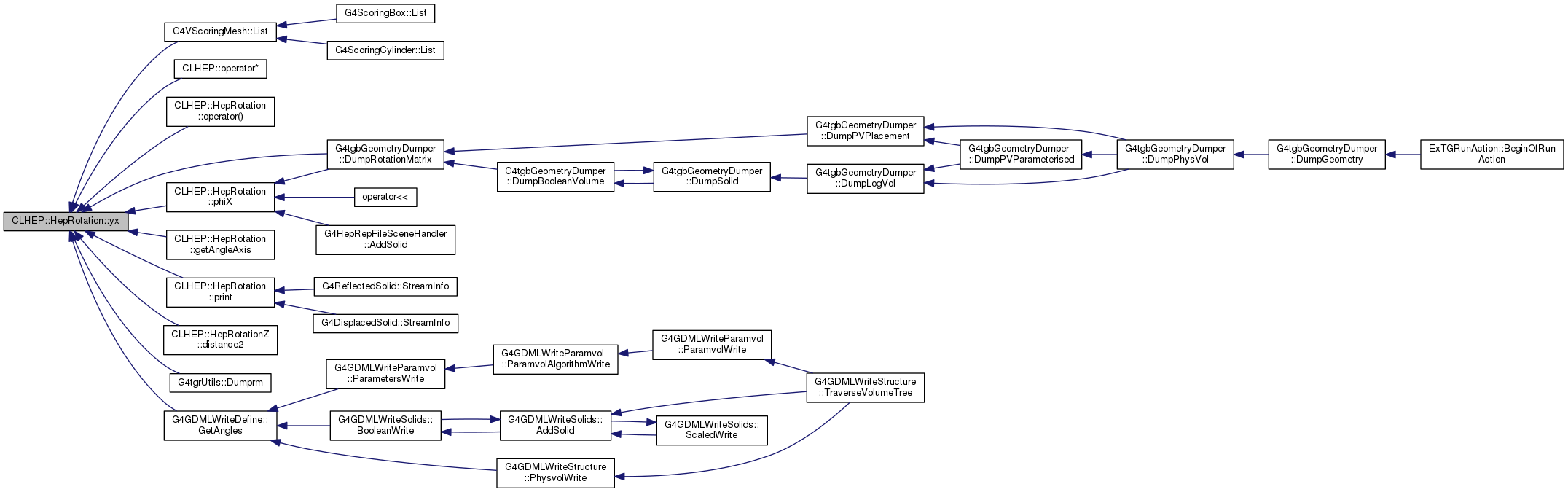
| double | yx () const |
| |
| double | yy () const |
| |
| double | yz () const |
| |
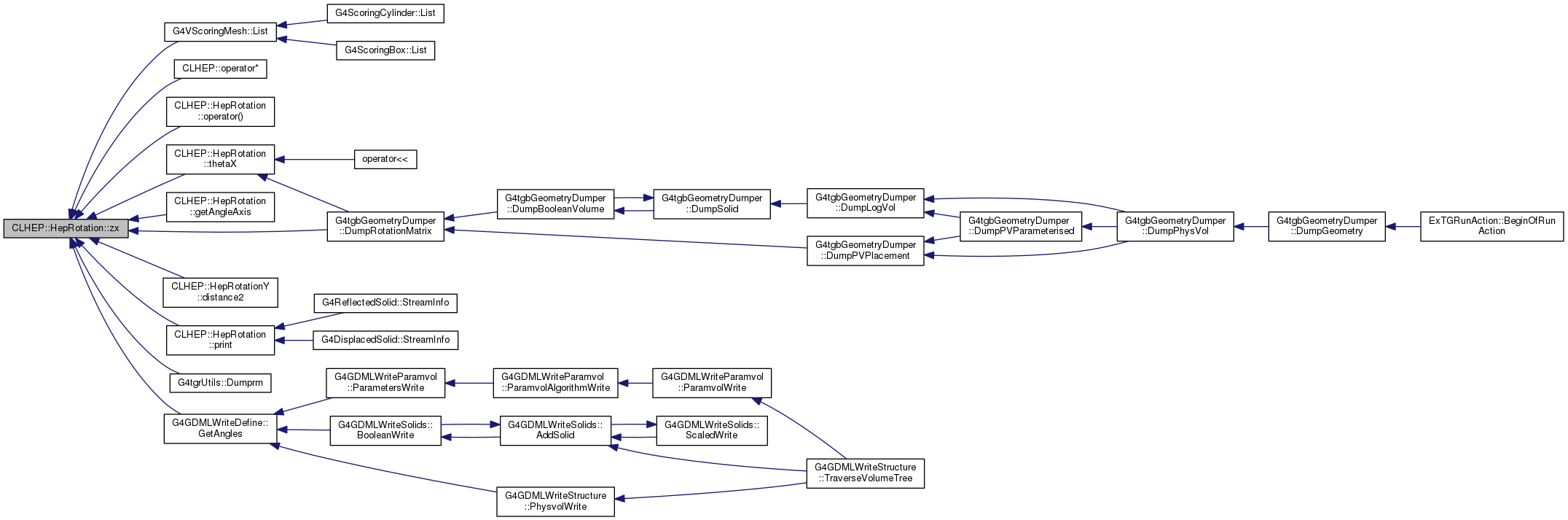
| double | zx () const |
| |
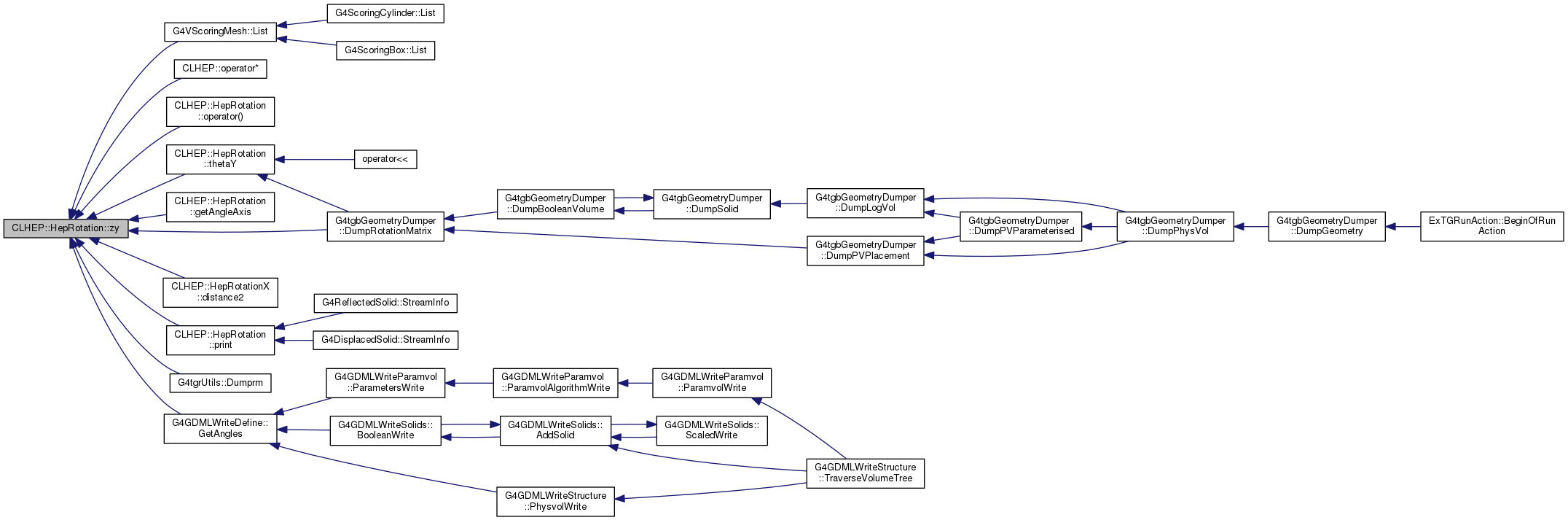
| double | zy () const |
| |
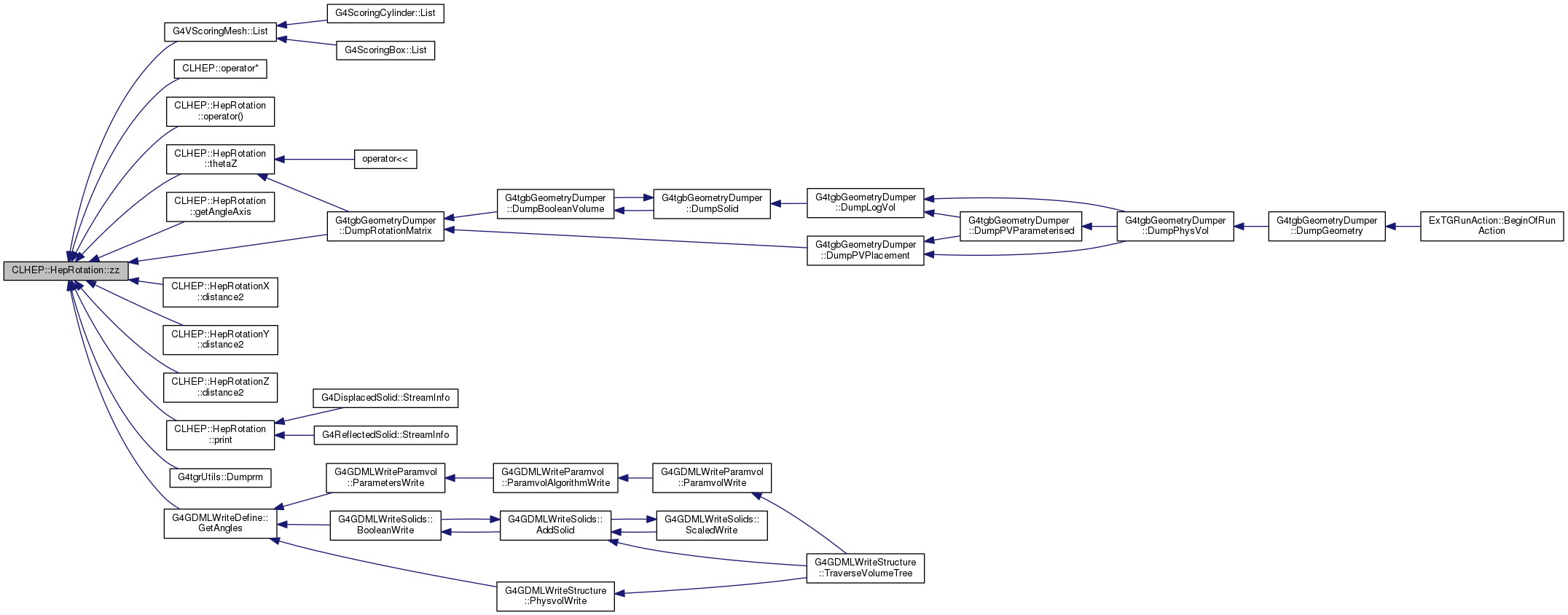
| double | zz () const |
| |
| HepRep3x3 | rep3x3 () const |
| |
| const HepRotation_row | operator[] (int) const |
| |
| double | operator() (int, int) const |
| |
| double | getPhi () const |
| |
| double | getTheta () const |
| |
| double | getPsi () const |
| |
| double | phi () const |
| |
| double | theta () const |
| |
| double | psi () const |
| |
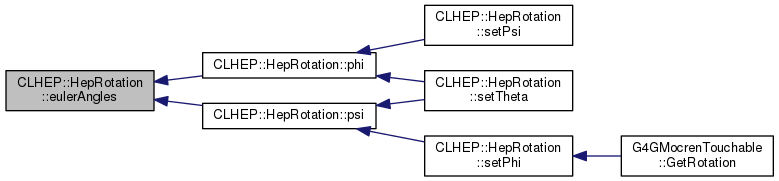
| HepEulerAngles | eulerAngles () const |
| |
| double | getDelta () const |
| |
| Hep3Vector | getAxis () const |
| |
| double | delta () const |
| |
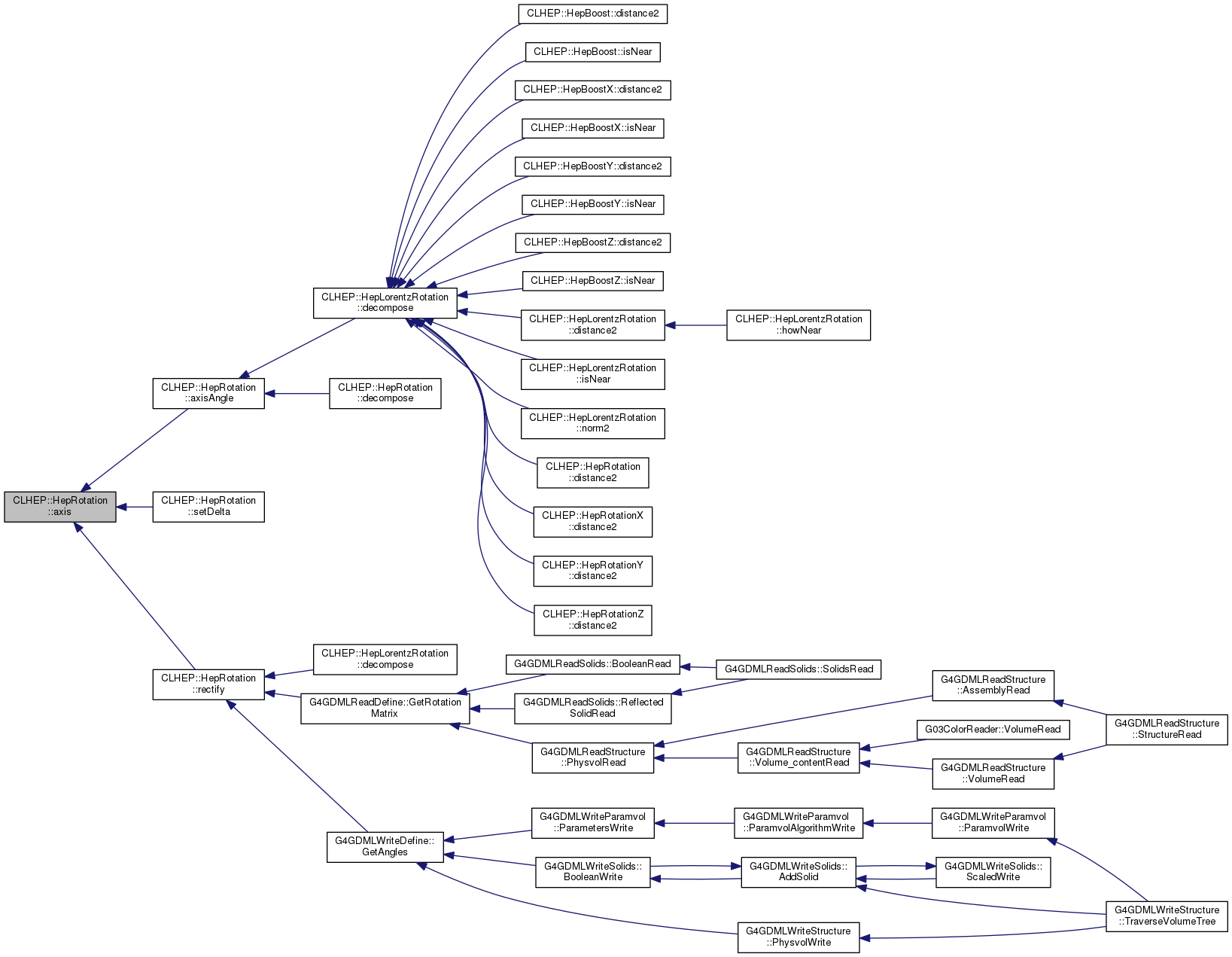
| Hep3Vector | axis () const |
| |
| HepAxisAngle | axisAngle () const |
| |
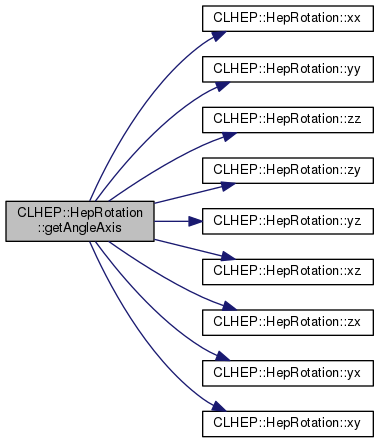
| void | getAngleAxis (double &delta, Hep3Vector &axis) const |
| |
| double | phiX () const |
| |
| double | phiY () const |
| |
| double | phiZ () const |
| |
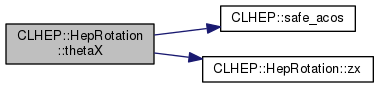
| double | thetaX () const |
| |
| double | thetaY () const |
| |
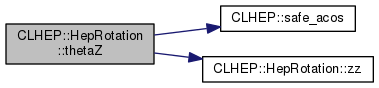
| double | thetaZ () const |
| |
| HepLorentzVector | col1 () const |
| |
| HepLorentzVector | col2 () const |
| |
| HepLorentzVector | col3 () const |
| |
| HepLorentzVector | col4 () const |
| |
| HepLorentzVector | row1 () const |
| |
| HepLorentzVector | row2 () const |
| |
| HepLorentzVector | row3 () const |
| |
| HepLorentzVector | row4 () const |
| |
| double | xt () const |
| |
| double | yt () const |
| |
| double | zt () const |
| |
| double | tx () const |
| |
| double | ty () const |
| |
| double | tz () const |
| |
| double | tt () const |
| |
| HepRep4x4 | rep4x4 () const |
| |
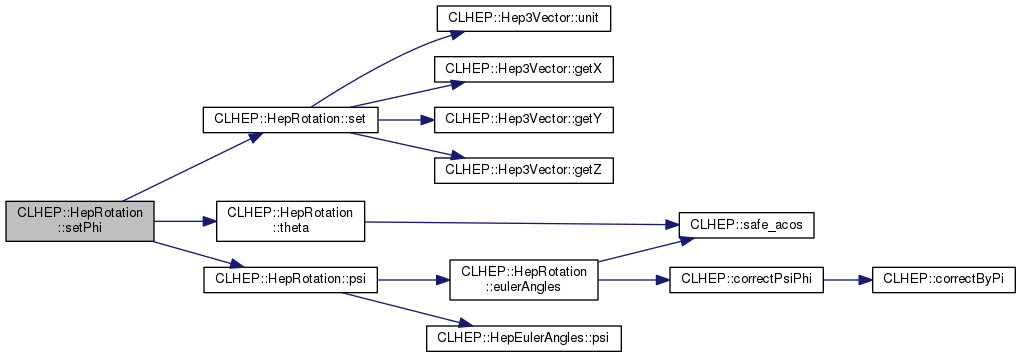
| void | setPhi (double phi) |
| |
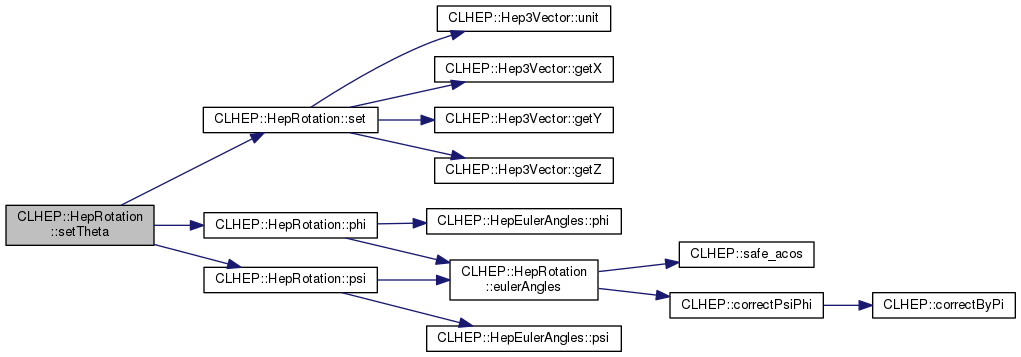
| void | setTheta (double theta) |
| |
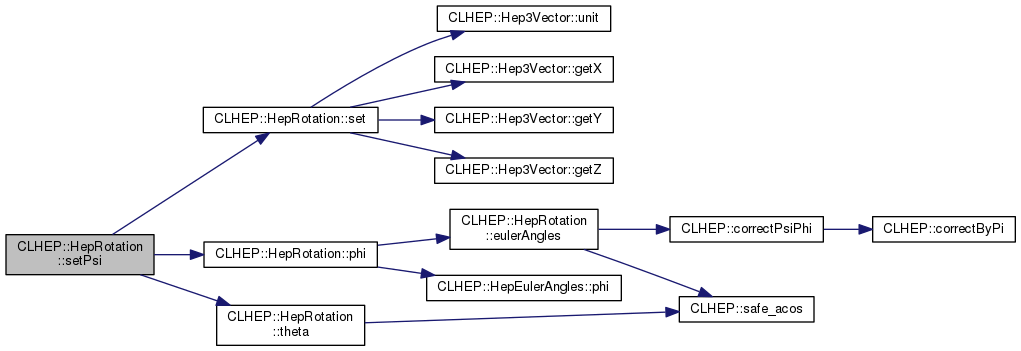
| void | setPsi (double psi) |
| |
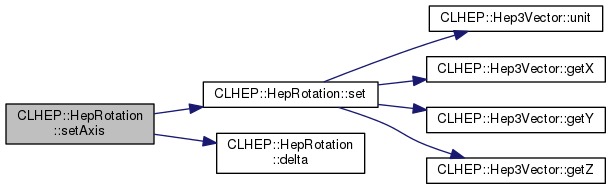
| void | setAxis (const Hep3Vector &axis) |
| |
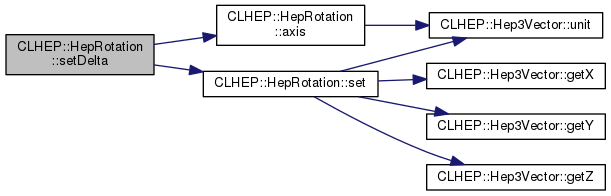
| void | setDelta (double delta) |
| |
| void | decompose (HepAxisAngle &rotation, Hep3Vector &boost) const |
| |
| void | decompose (Hep3Vector &boost, HepAxisAngle &rotation) const |
| |
| bool | isIdentity () const |
| |
| int | compare (const HepRotation &r) const |
| |
| bool | operator== (const HepRotation &r) const |
| |
| bool | operator!= (const HepRotation &r) const |
| |
| bool | operator< (const HepRotation &r) const |
| |
| bool | operator> (const HepRotation &r) const |
| |
| bool | operator<= (const HepRotation &r) const |
| |
| bool | operator>= (const HepRotation &r) const |
| |
| double | distance2 (const HepRotation &r) const |
| |
| double | howNear (const HepRotation &r) const |
| |
| bool | isNear (const HepRotation &r, double epsilon=Hep4RotationInterface::tolerance) const |
| |
| double | distance2 (const HepBoost <) const |
| |
| double | distance2 (const HepLorentzRotation <) const |
| |
| double | howNear (const HepBoost <) const |
| |
| double | howNear (const HepLorentzRotation <) const |
| |
| bool | isNear (const HepBoost <, double epsilon=Hep4RotationInterface::tolerance) const |
| |
| bool | isNear (const HepLorentzRotation <, double epsilon=Hep4RotationInterface::tolerance) const |
| |
| double | norm2 () const |
| |
| void | rectify () |
| |
| Hep3Vector | operator() (const Hep3Vector &p) const |
| |
| Hep3Vector | operator* (const Hep3Vector &p) const |
| |
| HepLorentzVector | operator() (const HepLorentzVector &w) const |
| |
| HepLorentzVector | operator* (const HepLorentzVector &w) const |
| |
| HepRotation | operator* (const HepRotation &r) const |
| |
| HepRotation | operator* (const HepRotationX &rx) const |
| |
| HepRotation | operator* (const HepRotationY &ry) const |
| |
| HepRotation | operator* (const HepRotationZ &rz) const |
| |
| HepRotation & | operator*= (const HepRotation &r) |
| |
| HepRotation & | transform (const HepRotation &r) |
| |
| HepRotation & | operator*= (const HepRotationX &r) |
| |
| HepRotation & | operator*= (const HepRotationY &r) |
| |
| HepRotation & | operator*= (const HepRotationZ &r) |
| |
| HepRotation & | transform (const HepRotationX &r) |
| |
| HepRotation & | transform (const HepRotationY &r) |
| |
| HepRotation & | transform (const HepRotationZ &r) |
| |
| HepRotation & | rotateX (double delta) |
| |
| HepRotation & | rotateY (double delta) |
| |
| HepRotation & | rotateZ (double delta) |
| |
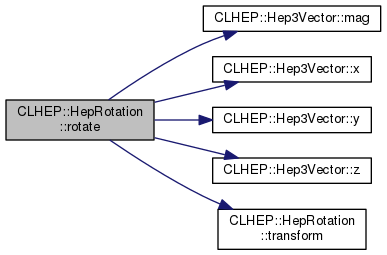
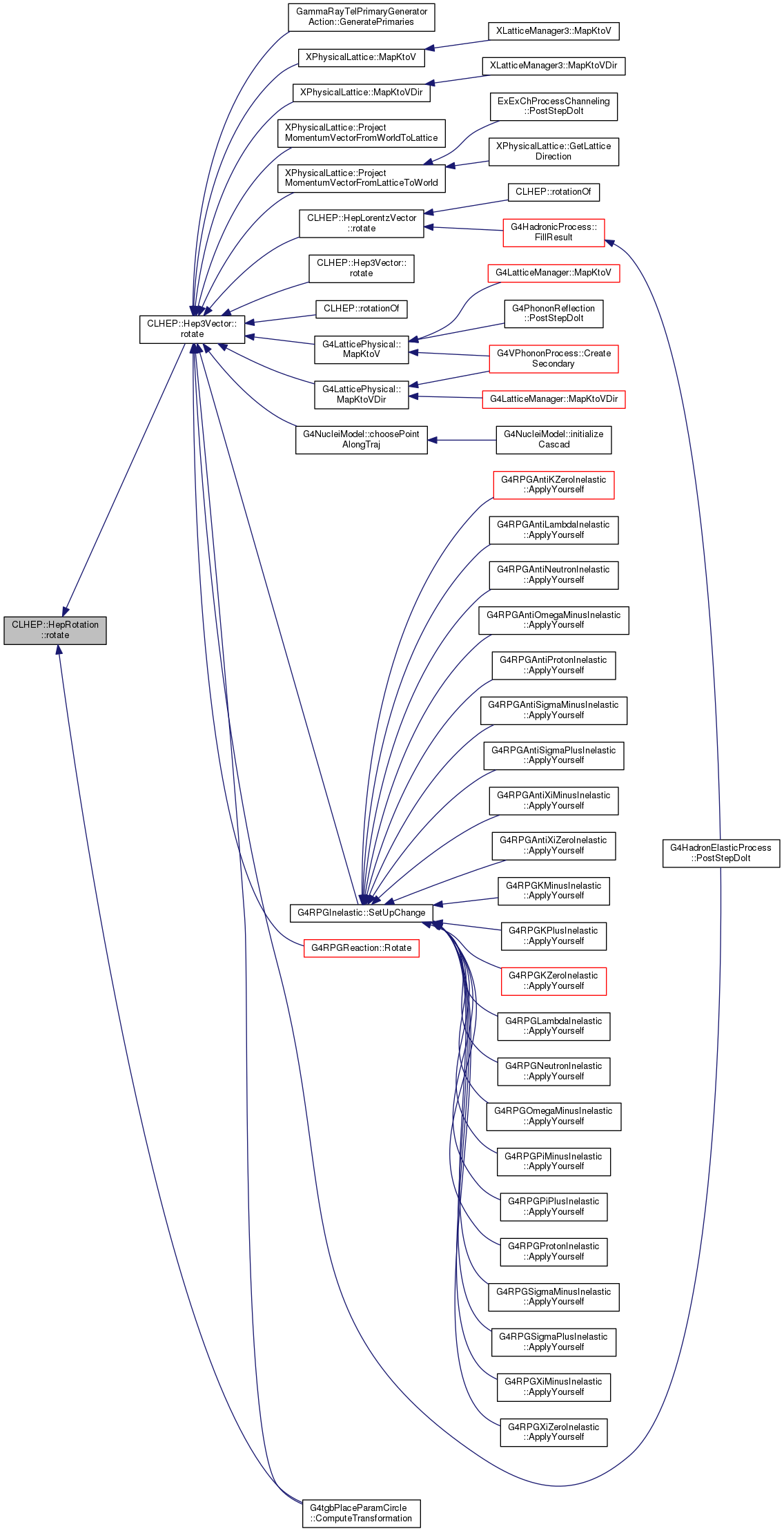
| HepRotation & | rotate (double delta, const Hep3Vector &axis) |
| |
| HepRotation & | rotate (double delta, const Hep3Vector *axis) |
| |
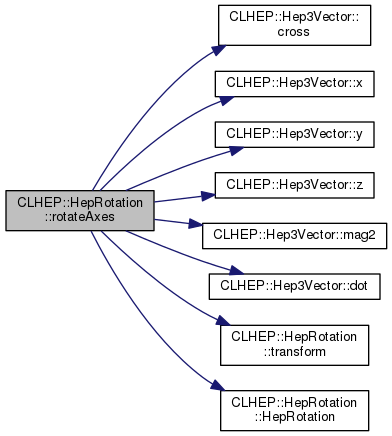
| HepRotation & | rotateAxes (const Hep3Vector &newX, const Hep3Vector &newY, const Hep3Vector &newZ) |
| |
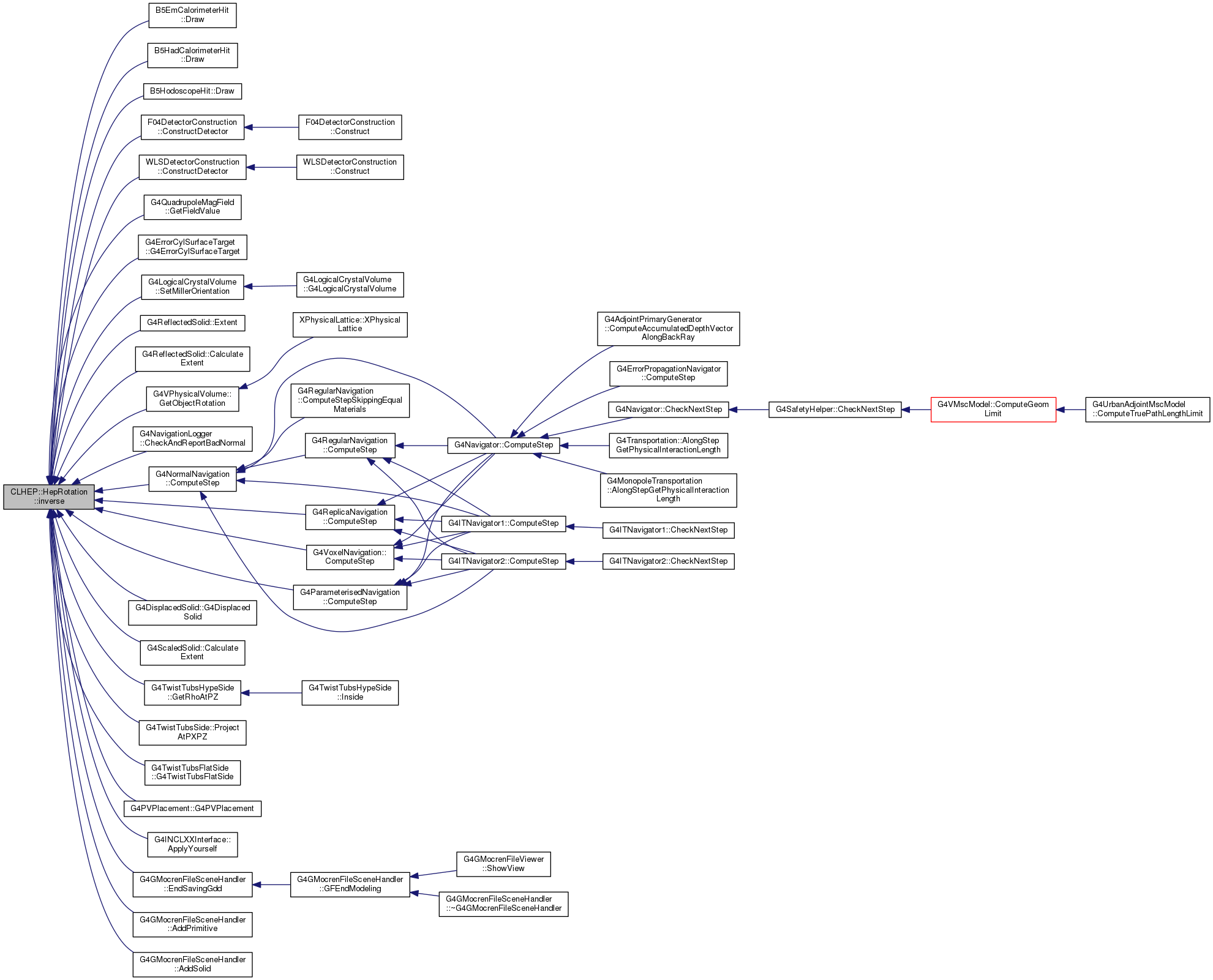
| HepRotation | inverse () const |
| |
| HepRotation & | invert () |
| |
| std::ostream & | print (std::ostream &os) const |
| |
- Author
Definition at line 47 of file Rotation.h.