|
Geant4
10.03.p01
|
|
Geant4
10.03.p01
|
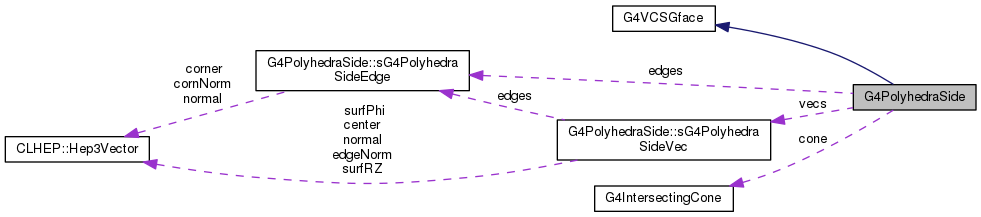
#include <G4PolyhedraSide.hh>
Classes | |
| struct | sG4PolyhedraSideEdge |
| struct | sG4PolyhedraSideVec |
Public Types | |
| typedef struct G4PolyhedraSide::sG4PolyhedraSideEdge | G4PolyhedraSideEdge |
| typedef struct G4PolyhedraSide::sG4PolyhedraSideVec | G4PolyhedraSideVec |
Static Public Member Functions | |
| static const G4PhSideManager & | GetSubInstanceManager () |
Protected Member Functions | |
| G4bool | IntersectSidePlane (const G4ThreeVector &p, const G4ThreeVector &v, const G4PolyhedraSideVec &vec, G4double normSign, G4double surfTolerance, G4double &distance, G4double &distFromSurface) |
| G4int | LineHitsSegments (const G4ThreeVector &p, const G4ThreeVector &v, G4int *i1, G4int *i2) |
| G4int | ClosestPhiSegment (G4double phi) |
| G4int | PhiSegment (G4double phi) |
| G4double | GetPhi (const G4ThreeVector &p) |
| G4double | DistanceToOneSide (const G4ThreeVector &p, const G4PolyhedraSideVec &vec, G4double *normDist) |
| G4double | DistanceAway (const G4ThreeVector &p, const G4PolyhedraSideVec &vec, G4double *normDist) |
| void | CopyStuff (const G4PolyhedraSide &source) |
Protected Attributes | |
| G4int | numSide |
| G4double | r [2] |
| G4double | z [2] |
| G4double | startPhi |
| G4double | deltaPhi |
| G4double | endPhi |
| G4bool | phiIsOpen |
| G4bool | allBehind |
| G4IntersectingCone * | cone |
| G4PolyhedraSideVec * | vecs |
| G4PolyhedraSideEdge * | edges |
| G4double | lenRZ |
| G4double | lenPhi [2] |
| G4double | edgeNorm |
Friends | |
| struct | sG4PolyhedraSideVec |
Definition at line 98 of file G4PolyhedraSide.hh.
| G4PolyhedraSide::G4PolyhedraSide | ( | const G4PolyhedraSideRZ * | prevRZ, |
| const G4PolyhedraSideRZ * | tail, | ||
| const G4PolyhedraSideRZ * | head, | ||
| const G4PolyhedraSideRZ * | nextRZ, | ||
| G4int | numSide, | ||
| G4double | phiStart, | ||
| G4double | phiTotal, | ||
| G4bool | phiIsOpen, | ||
| G4bool | isAllBehind = false |
||
| ) |
Definition at line 72 of file G4PolyhedraSide.cc.
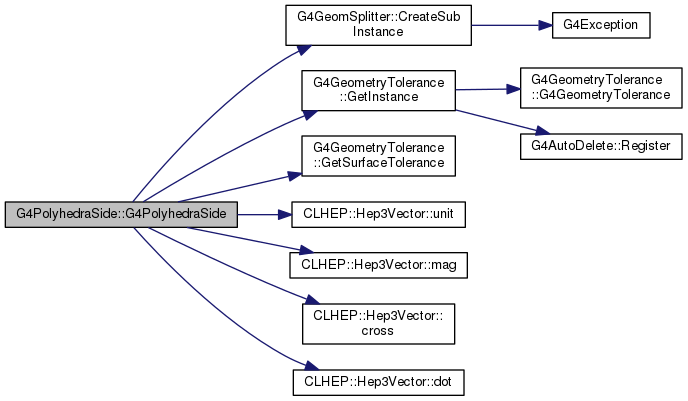

|
virtual |
Definition at line 330 of file G4PolyhedraSide.cc.
| G4PolyhedraSide::G4PolyhedraSide | ( | const G4PolyhedraSide & | source | ) |
Definition at line 341 of file G4PolyhedraSide.cc.

| G4PolyhedraSide::G4PolyhedraSide | ( | __void__ & | ) |
Definition at line 316 of file G4PolyhedraSide.cc.
|
virtual |
Implements G4VCSGface.
Definition at line 730 of file G4PolyhedraSide.cc.
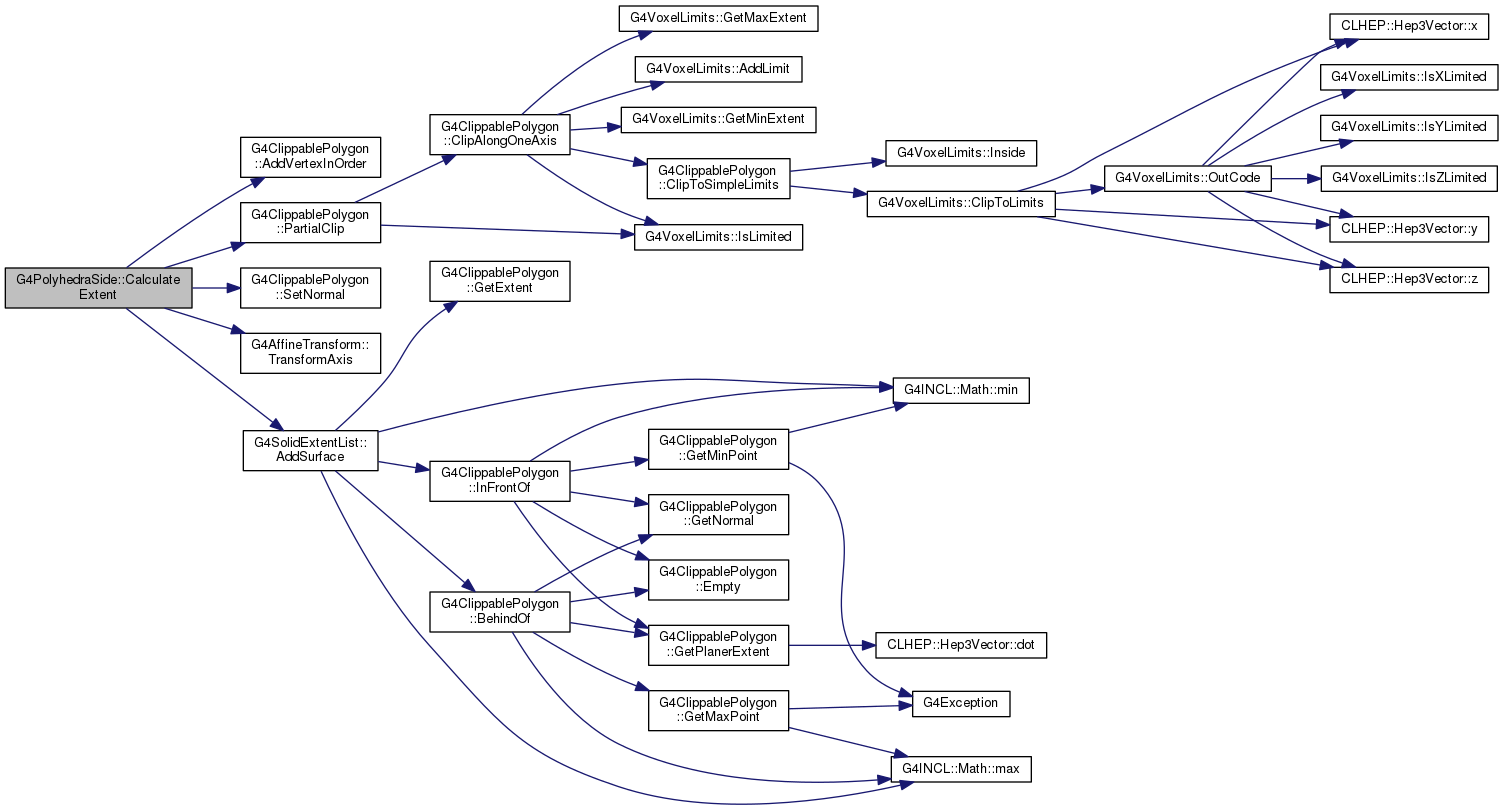
|
inlinevirtual |
Implements G4VCSGface.
Definition at line 134 of file G4PolyhedraSide.hh.
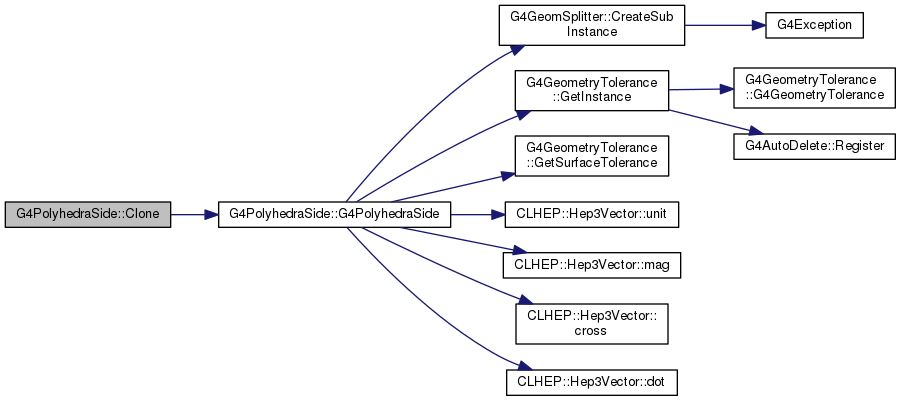
Definition at line 942 of file G4PolyhedraSide.cc.

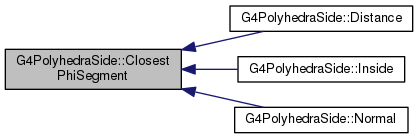
|
protected |
Definition at line 370 of file G4PolyhedraSide.cc.

|
virtual |
Implements G4VCSGface.
Definition at line 585 of file G4PolyhedraSide.cc.
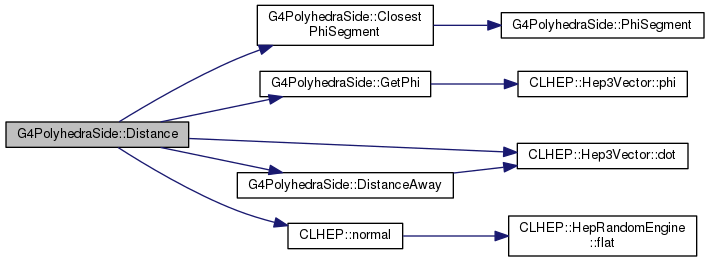
|
protected |
Definition at line 1063 of file G4PolyhedraSide.cc.


|
protected |
Definition at line 1039 of file G4PolyhedraSide.cc.

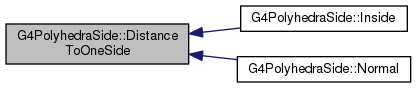
|
virtual |
Implements G4VCSGface.
Definition at line 670 of file G4PolyhedraSide.cc.
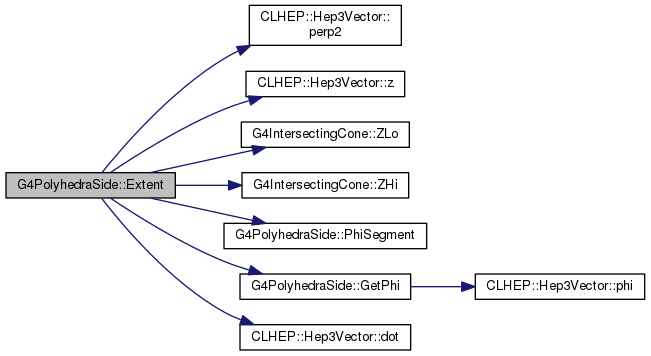
|
inline |
Definition at line 157 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 1012 of file G4PolyhedraSide.cc.

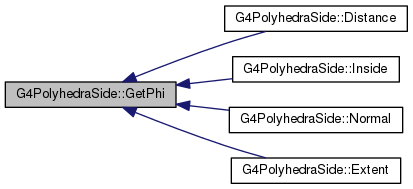
|
virtual |
Implements G4VCSGface.
Definition at line 1289 of file G4PolyhedraSide.cc.

| G4ThreeVector G4PolyhedraSide::GetPointOnPlane | ( | G4ThreeVector | p0, |
| G4ThreeVector | p1, | ||
| G4ThreeVector | p2, | ||
| G4ThreeVector | p3, | ||
| G4double * | Area | ||
| ) |
Definition at line 1232 of file G4PolyhedraSide.cc.

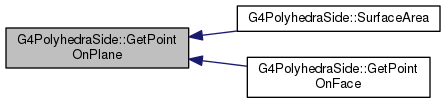
|
static |
|
virtual |
Implements G4VCSGface.
Definition at line 618 of file G4PolyhedraSide.cc.
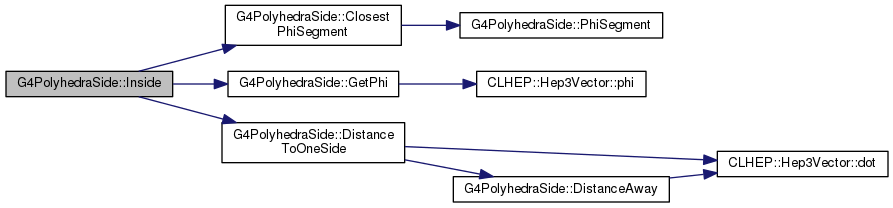
|
virtual |
Implements G4VCSGface.
Definition at line 466 of file G4PolyhedraSide.cc.
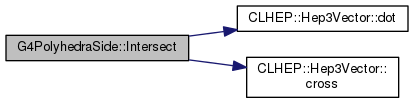
|
protected |
Definition at line 801 of file G4PolyhedraSide.cc.
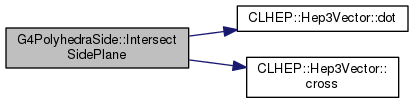
|
protected |
Definition at line 896 of file G4PolyhedraSide.cc.
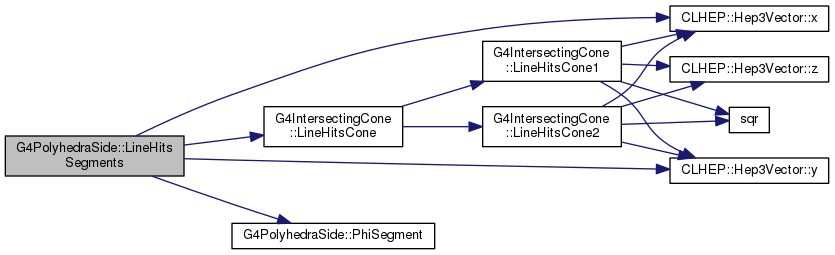
|
virtual |
Implements G4VCSGface.
Definition at line 649 of file G4PolyhedraSide.cc.
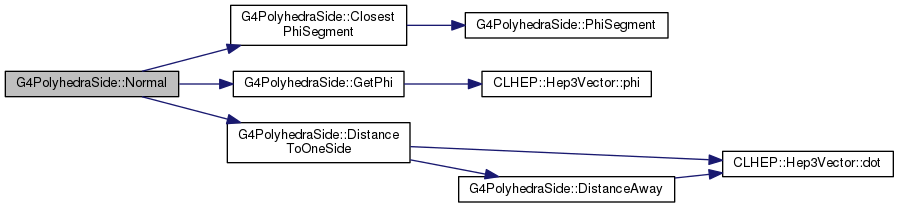
| G4PolyhedraSide & G4PolyhedraSide::operator= | ( | const G4PolyhedraSide & | source | ) |
Definition at line 353 of file G4PolyhedraSide.cc.

|
virtual |
Implements G4VCSGface.
Definition at line 1254 of file G4PolyhedraSide.cc.

| G4double G4PolyhedraSide::SurfaceTriangle | ( | G4ThreeVector | p1, |
| G4ThreeVector | p2, | ||
| G4ThreeVector | p3, | ||
| G4ThreeVector * | p4 | ||
| ) |
Definition at line 1209 of file G4PolyhedraSide.cc.

|
friend |
Definition at line 166 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 224 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 226 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 220 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 232 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 229 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 220 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 230 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 230 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 218 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 223 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 219 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 220 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 228 of file G4PolyhedraSide.hh.
|
protected |
Definition at line 219 of file G4PolyhedraSide.hh.