G4GoudsmitSaundersonTable Class Reference

#include <G4GoudsmitSaundersonTable.hh>

Public Member Functions
	G4GoudsmitSaundersonTable ()
	~G4GoudsmitSaundersonTable ()
void	Initialise ()
G4double	SampleCosTheta (G4double, G4double, G4double, G4double, G4double, G4double)
G4double	SampleCosThetaII (G4double, G4double, G4double, G4double, G4double, G4double)
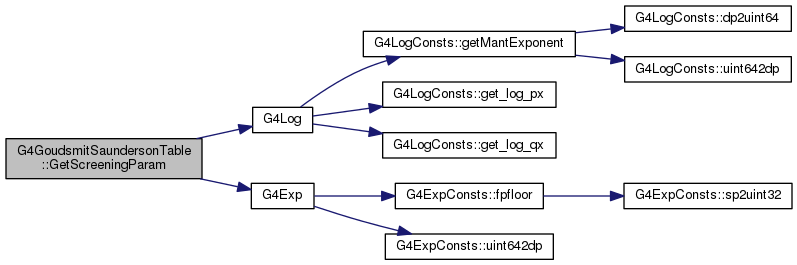
G4double	GetScreeningParam (G4double)
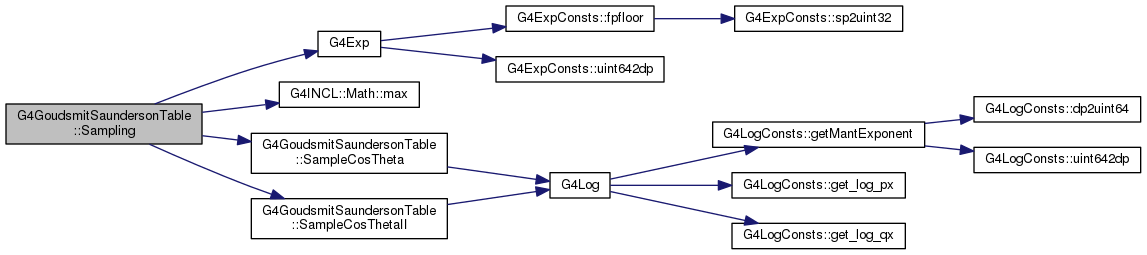
void	Sampling (G4double, G4double, G4double, G4double &, G4double &)
G4double	GetMoliereBc (G4int matindx)
G4double	GetMoliereXc2 (G4int matindx)

Detailed Description

Definition at line 72 of file G4GoudsmitSaundersonTable.hh.

Constructor & Destructor Documentation

G4GoudsmitSaundersonTable::G4GoudsmitSaundersonTable ( )

inline

Definition at line 76 of file G4GoudsmitSaundersonTable.hh.

{};

G4GoudsmitSaundersonTable::~G4GoudsmitSaundersonTable

(

)

Definition at line 299 of file G4GoudsmitSaundersonTable.cc.

                                                     {
  if(fgMoliereBc){
    delete fgMoliereBc;
    fgMoliereBc = 0;
  }
  if(fgMoliereXc2){
    delete fgMoliereXc2;
    fgMoliereXc2 = 0;
  }
  fgIsInitialised = FALSE;
}

Member Function Documentation

G4double G4GoudsmitSaundersonTable::GetMoliereBc ( G4int  matindx )

inline

Definition at line 104 of file G4GoudsmitSaundersonTable.hh.

{return (*fgMoliereBc)[matindx];}

Here is the caller graph for this function:

G4double G4GoudsmitSaundersonTable::GetMoliereXc2 ( G4int  matindx )

inline

Definition at line 105 of file G4GoudsmitSaundersonTable.hh.

{return (*fgMoliereXc2)[matindx];}

Here is the caller graph for this function:

G4double G4GoudsmitSaundersonTable::GetScreeningParam

(

G4double

G1

)

Definition at line 563 of file G4GoudsmitSaundersonTable.cc.

                                                                {
   if(G1<fgG1Values[0])                      return fgScreeningParam[0];
   if(G1>fgG1Values[fgNumScreeningParams-1]) return fgScreeningParam[fgNumScreeningParams-1];
   // normal case
   const G4double lng10   = -2.30258509299405e+01;   //log(fgG1Values[0]);
   const G4double invlng1 =  6.948711710452e+00;     //1./log(fgG1Values[i+1]/fgG1Values[i])
   G4double logG1 = G4Log(G1);
   G4int k = (G4int)((logG1-lng10)*invlng1);
 return G4Exp(logG1*fgSrcAValues[k])*fgSrcBValues[k]; // log-log linear
}

Here is the call graph for this function:

Here is the caller graph for this function:

void G4GoudsmitSaundersonTable::Initialise

(

)

Definition at line 288 of file G4GoudsmitSaundersonTable.cc.

                                          {
   if(!fgIsInitialised){
     LoadMSCData();
     LoadMSCDataII();
     fgIsInitialised = TRUE;
   }

   InitMoliereMSCParams();
}

Here is the caller graph for this function:

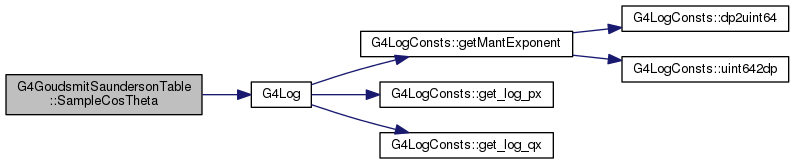
G4double G4GoudsmitSaundersonTable::SampleCosTheta	(	G4double	lambdavalue,
		G4double	lamG1value,
		G4double	screeningparam,
		G4double	rndm1,
		G4double	rndm2,
		G4double	rndm3
	)

Definition at line 314 of file G4GoudsmitSaundersonTable.cc.

                                           {
  const G4double lnl0   = 0.0;              //log(fgLambdaValues[0]);
  const G4double invlnl = 6.5144172285e+00; //1./log(fgLambdaValues[i+1]/fgLambdaValues[i])
  G4double logLambdaVal = G4Log(lambdavalue);
  G4int lambdaindx = (G4int)((logLambdaVal-lnl0)*invlnl);

  const G4double dd = 1.0/0.0499; // delta
  G4int lamg1indx  = (G4int)((lamG1value-fgLamG1Values[0])*dd);

  G4double probOfLamJ = G4Log(fgLambdaValues[lambdaindx+1]/lambdavalue)*invlnl;
  if(rndm1 > probOfLamJ)
     ++lambdaindx;

  // store 1.0/(fgLamG1Values[lamg1indx+1]-fgLamG1Values[lamg1indx]) const value
  const G4double onePerLamG1Diff = dd;
  G4double probOfLamG1J = (fgLamG1Values[lamg1indx+1]-lamG1value)*onePerLamG1Diff;
  if(rndm2 > probOfLamG1J)
     ++lamg1indx;

  G4int begin = lambdaindx*(fgNumLamG1*fgNumUvalues)+lamg1indx*fgNumUvalues;

  // sample bin
  G4int indx =  (G4int)(rndm3*100); // value/delatU ahol deltaU = 0.01; find u-indx
  G4double cp1 = fgUValues[indx];
//  G4double cp2 = fgUValues[indx+1];
  indx +=begin;

  G4double u1  = fgInverseQ2CDFs[indx];
  G4double u2  = fgInverseQ2CDFs[indx+1];

  G4double dum1 = rndm3 - cp1;
  const G4double dum2  = 0.01;//cp2-cp1;  // this is constans 0.01
  const G4double dum22 = 0.0001;
  // rational interpolation of the inverse CDF
  G4double sample= u1+(1.0+fgInterParamsA2[indx]+fgInterParamsB2[indx])*dum1*dum2/(dum22+
               dum1*dum2*fgInterParamsA2[indx]+fgInterParamsB2[indx]*dum1*dum1)*(u2-u1);

  // transform back u to cos(theta) :
  // -compute parameter value a = w2*screening_parameter
  G4double t = logLambdaVal;
  G4double dum;
  if(lambdavalue >= 10.0)
    dum = 0.5*(-2.77164+t*( 2.94874-t*(0.1535754-t*0.00552888) ));
  else
    dum = 0.5*(1.347+t*(0.209364-t*(0.45525-t*(0.50142-t*0.081234))));

  G4double a = dum*(lambdavalue+4.0)*screeningparam;

  // this is the sampled cos(theta)
  return (2.0*a*sample)/(1.0-sample+a);
}

Here is the call graph for this function:

Here is the caller graph for this function:

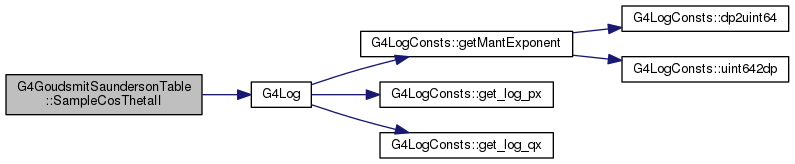
G4double G4GoudsmitSaundersonTable::SampleCosThetaII	(	G4double	lambdavalue,
		G4double	lamG1value,
		G4double	screeningparam,
		G4double	rndm1,
		G4double	rndm2,
		G4double	rndm3
	)

Definition at line 371 of file G4GoudsmitSaundersonTable.cc.

                                           {
  const G4double lnl0   = 0.0;              //log(fgLambdaValues[0]);
  const G4double invlnl = 6.5144172285e+00; //1./log(fgLambdaValues[i+1]/fgLambdaValues[i])
  G4double logLambdaVal = G4Log(lambdavalue);
  G4int lambdaindx = (G4int)((logLambdaVal-lnl0)*invlnl);

  const G4double dd = 1.0/0.333; // delta
  G4int lamg1indx  = (G4int)((lamG1value-fgLamG1ValuesII[0])*dd);

  G4double probOfLamJ = G4Log(fgLambdaValues[lambdaindx+1]/lambdavalue)*invlnl;
  if(rndm1 > probOfLamJ)
     ++lambdaindx;

  // store 1.0/(fgLamG1Values[lamg1indx+1]-fgLamG1Values[lamg1indx]) const value
  const G4double onePerLamG1Diff = dd;
  G4double probOfLamG1J = (fgLamG1ValuesII[lamg1indx+1]-lamG1value)*onePerLamG1Diff;
  if(rndm2 > probOfLamG1J)
     ++lamg1indx;

  // protection against cases when the sampled lamG1 values are not possible due
  // to the fact that G1<=1 (G1 = lam_el/lam_tr1)
  // -- in theory it should never happen when lamg1indx=0 but check it just to be sure
  if(fgLamG1ValuesII[lamg1indx]>lambdavalue && lamg1indx>0) 
    --lamg1indx;
    

  G4int begin = lambdaindx*(fgNumLamG1II*fgNumUvalues)+lamg1indx*fgNumUvalues;

  // sample bin
  G4int indx =  (G4int)(rndm3*100); // value/delatU ahol deltaU = 0.01; find u-indx
  G4double cp1 = fgUValues[indx];
//  G4double cp2 = fgUValues[indx+1];
  indx +=begin;

  G4double u1  = fgInverseQ2CDFsII[indx];
  G4double u2  = fgInverseQ2CDFsII[indx+1];

  G4double dum1 = rndm3 - cp1;
  const G4double dum2  = 0.01;//cp2-cp1;  // this is constans 0.01
  const G4double dum22 = 0.0001;
  // rational interpolation of the inverse CDF
  G4double sample= u1+(1.0+fgInterParamsA2II[indx]+fgInterParamsB2II[indx])*dum1*dum2/(dum22+
               dum1*dum2*fgInterParamsA2II[indx]+fgInterParamsB2II[indx]*dum1*dum1)*(u2-u1);

  // transform back u to cos(theta) :
  // -compute parameter value a = w2*screening_parameter
  G4double t = logLambdaVal;
  G4double dum = 0.;
  if(lambdavalue >= 10.0)
    dum = 0.5*(-2.77164+t*( 2.94874-t*(0.1535754-t*0.00552888) ));
  else
    dum = 0.5*(1.347+t*(0.209364-t*(0.45525-t*(0.50142-t*0.081234))));

  G4double a = dum*(lambdavalue+4.0)*screeningparam;

  // this is the sampled cos(theta)
  return (2.0*a*sample)/(1.0-sample+a);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void G4GoudsmitSaundersonTable::Sampling	(	G4double	lambdavalue,
		G4double	lamG1value,
		G4double	scrPar,
		G4double &	cost,
		G4double &	sint
	)

**** let it izotropic if we are above the grid i.e. true path length is long

Definition at line 435 of file G4GoudsmitSaundersonTable.cc.

                                                                            {
  G4double rand0 = G4UniformRand();
  G4double expn  = G4Exp(-lambdavalue);

  //
  // no scattering case
  //
  if(rand0 < expn) {
    cost = 1.0;
    sint = 0.0;
    return;
  }

  //
  // single scattering case : sample (analitically) from the single scattering PDF
  //                          that corresponds to the modified-Wentzel DCS i.e.
  //                          Wentzel DCS that gives back the PWA first-transport mfp
  //
  if( rand0 < (1.+lambdavalue)*expn) {
    G4double rand1 = G4UniformRand();
    // sampling 1-cos(theta)
    G4double dum0  = 2.0*scrPar*rand1/(1.0 - rand1 + scrPar);
    // add protections
    if(dum0 < 0.0)       dum0 = 0.0;
    else if(dum0 > 2.0 ) dum0 = 2.0;
    // compute cos(theta) and sin(theta)
    cost = 1.0 - dum0;
    sint = std::sqrt(dum0*(2.0 - dum0));
    return;
  }

  //
  // handle this case:
  //      -lambdavalue < 1 i.e. mean #elastic events along the step is < 1 but
  //       the currently sampled case is not 0 or 1 scattering. [Our minimal
  //       lambdavalue (that we have precomputed, transformed angular distributions
  //       stored in a form of equally probabe intervalls together with rational
  //       interp. parameters) is 1.]
  //      -probability of having n elastic events follows Poisson stat. with
  //       lambdavalue parameter.
  //      -the max. probability (when lambdavalue=1) of having more than one
  //       elastic events is 0.2642411 and the prob of having 2,3,..,n elastic
  //       events decays rapidly with n. So set a max n to 10.
  //      -sampling of this cases is done in a one-by-one single elastic event way
  //       where the current #elastic event is sampled from the Poisson distr.
  //      -(other possibility would be to use lambdavalue=1 distribution because
  //        they are very close)
  if(lambdavalue < 1.0) {
     G4double prob, cumprob;
     prob = cumprob = expn;
     G4double curcost,cursint;
     // init cos(theta) and sin(theta) to the zero scattering values
     cost = 1.0;
     sint = 0.0;

     for(G4int iel = 1; iel < 10; ++iel){
        // prob of having iel scattering from Poisson
        prob    *= lambdavalue/(G4double)iel;
        cumprob += prob;
        //
        //sample cos(theta) from the singe scattering pdf
        //
        G4double rand1 = G4UniformRand();
        // sampling 1-cos(theta)
        G4double dum0  = 2.0*scrPar*rand1/(1.0 - rand1 + scrPar);
        // compute cos(theta) and sin(theta)
        curcost = 1.0 - dum0;
        cursint = dum0*(2.0 - dum0);
        //
        // if we got current deflection that is not too small
        // then update cos(theta) sin(theta)
        if(cursint > 1.0e-20){
          cursint = std::sqrt(cursint);
          G4double curphi = CLHEP::twopi*G4UniformRand();
          cost = cost*curcost - sint*cursint*std::cos(curphi);
          sint = std::sqrt(std::max(0.0, (1.0-cost)*(1.0+cost)));
        }
        //
        // check if we have done enough scattering i.e. sampling from the Poisson
        if( rand0 < cumprob)
          return;
     }
     // if reached the max iter i.e. 10
     return;
  }


  //  IT IS DONE NOW IN THE MODEL
  //if(lamG1value>fgLamG1Values[fgNumLamG1-1]) {
  //  cost = 1.-2.*G4UniformRand();
  //  sint = std::sqrt((1.-cost)*(1.+cost));
  //  return;
  //}


  //
  // multiple scattering case with lambdavalue >= 1:
  //   - use the precomputed and transformed Goudsmit-Saunderson angular
  //     distributions that are stored in a form of equally probabe intervalls
  //     together with the corresponding rational interp. parameters
  //
  // add protections
  if(lamG1value<fgLamG1Values[0]) lamG1value = fgLamG1Values[0];
  if(lamG1value>fgLamG1ValuesII[fgNumLamG1II-1]) lamG1value = fgLamG1ValuesII[fgNumLamG1II-1];

  // sample 1-cos(theta) :: depending on the grids
  G4double dum0 = 0.0;
  if(lamG1value<fgLamG1Values[fgNumLamG1-1]) {
      dum0 = SampleCosTheta(lambdavalue, lamG1value, scrPar, G4UniformRand(),
                                 G4UniformRand(), G4UniformRand());

  } else {
    dum0 = SampleCosThetaII(lambdavalue, lamG1value, scrPar, G4UniformRand(),
                               G4UniformRand(), G4UniformRand());
  }

  // add protections
  if(dum0 < 0.0)  dum0 = 0.0;
  if(dum0 > 2.0 ) dum0 = 2.0;

  // compute cos(theta) and sin(theta)
     cost = 1.0-dum0;
     sint = std::sqrt(dum0*(2.0 - dum0));
}

Here is the call graph for this function:

Here is the caller graph for this function:

---

The documentation for this class was generated from the following files:

• geant4.10.03.p01/source/processes/electromagnetic/standard/include/G4GoudsmitSaundersonTable.hh
• geant4.10.03.p01/source/processes/electromagnetic/standard/src/G4GoudsmitSaundersonTable.cc