nf_specialFunctions.h File Reference

#include <math.h>
#include <float.h>
#include <nf_utilities.h>

Include dependency graph for nf_specialFunctions.h:

This graph shows which files directly or indirectly include this file:

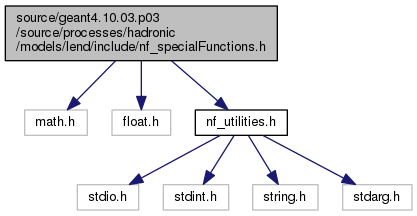
Go to the source code of this file.

Functions
double	nf_polevl (double x, double coef[], int N)
double	nf_p1evl (double x, double coef[], int N)
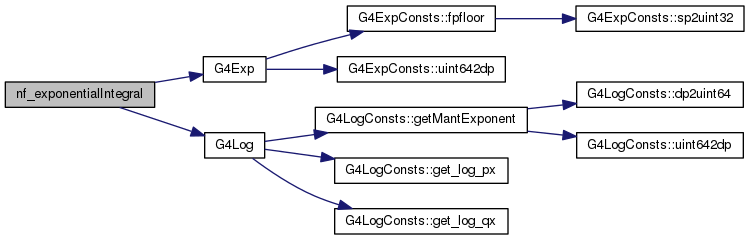
double	nf_exponentialIntegral (int n, double x, nfu_status *status)
double	nf_gammaFunction (double x, nfu_status *status)
double	nf_logGammaFunction (double x, nfu_status *status)
double	nf_incompleteGammaFunction (double a, double x, nfu_status *status)
double	nf_incompleteGammaFunctionComplementary (double a, double x, nfu_status *status)
double	nf_amc_log_factorial (int)
double	nf_amc_factorial (int)
double	nf_amc_wigner_3j (int, int, int, int, int, int)
double	nf_amc_wigner_6j (int, int, int, int, int, int)
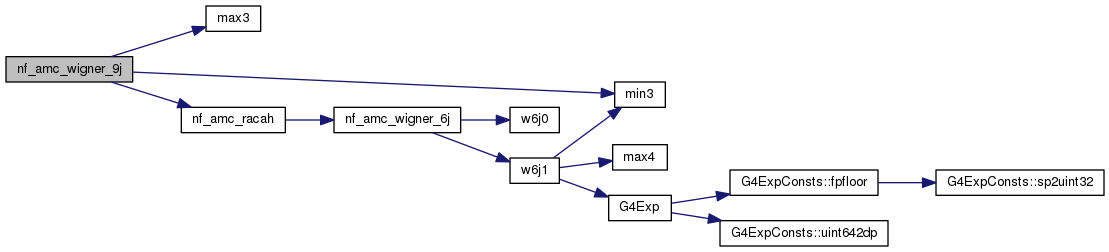
double	nf_amc_wigner_9j (int, int, int, int, int, int, int, int, int)
double	nf_amc_racah (int, int, int, int, int, int)
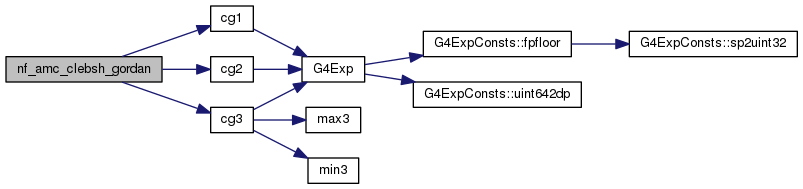
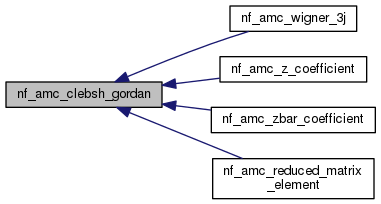
double	nf_amc_clebsh_gordan (int, int, int, int, int)
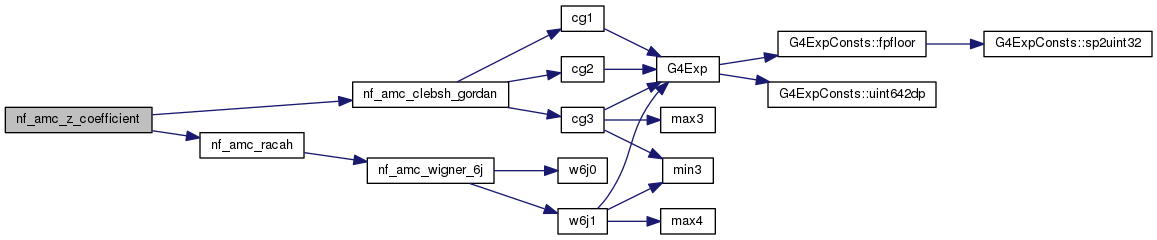
double	nf_amc_z_coefficient (int, int, int, int, int, int)
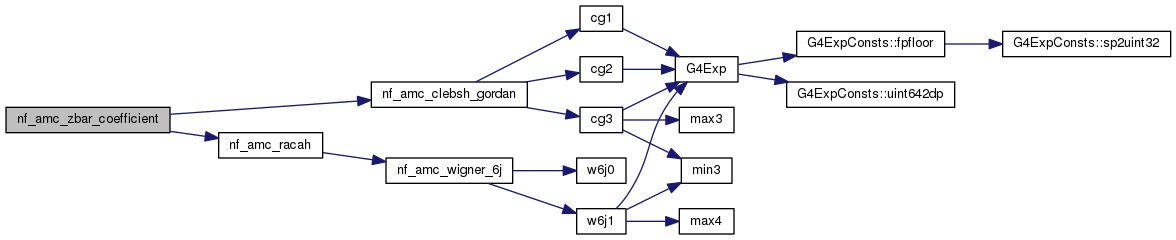
double	nf_amc_zbar_coefficient (int, int, int, int, int, int)
double	nf_amc_reduced_matrix_element (int, int, int, int, int, int, int)

Function Documentation

double nf_amc_clebsh_gordan	(	int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 288 of file nf_angularMomentumCoupling.cc.

                                                                      {
/*
*       Clebsh-Gordan coefficient 
*           = <j1,j2,m1,m2|j3,m1+m2>
*           = (-)^(j1-j2+m1+m2) * std::sqrt(2*j3+1) * / j1 j2   j3   \
*                                                \ m1 m2 -m1-m2 /
*
*   Note: Last value m3 is preset to m1+m2.  Any other value will evaluate to 0.0.
*/

    int m3, x1, x2, x3, y1, y2, y3;
    double cg = 0.0;

    if ( j1 < 0 || j2 < 0 || j3 < 0) return( 0.0 );
    if ( j1 + j2 + j3 > 2 * MAX_FACTORIAL ) return( INFINITY );

    m3 = m1 + m2;

    if ( ( x1 = ( j1 + m1 ) / 2 + 1 ) <= 0 ) return( 0.0 );
    if ( ( x2 = ( j2 + m2 ) / 2 + 1 ) <= 0 ) return( 0.0 );
    if ( ( x3 = ( j3 - m3 ) / 2 + 1 ) <= 0 ) return( 0.0 );

    if ( ( y1 = x1 - m1 ) <= 0 ) return( 0.0 );
    if ( ( y2 = x2 - m2 ) <= 0 ) return( 0.0 );
    if ( ( y3 = x3 + m3 ) <= 0 ) return( 0.0 );

    if ( j3 == 0 ){
        if ( j1 == j2 ) cg = ( 1.0 / std::sqrt( (double)j1 + 1.0 ) * ( ( y1 % 2 == 0 ) ? -1:1 ) );
    }
    else if ( (j1 == 0 || j2 == 0 ) ){
        if ( ( j1 + j2 ) == j3 ) cg = 1.0;
    }
    else {
        if( m3 == 0 && std::abs( m1 ) <= 1 ){
            if( m1 == 0 ) cg = cg1( x1, x2, x3 );
            else          cg = cg2( x1 + y1 - y2, x3 - 1, x1 + x2 - 2, x1 - y2, j1, j2, j3, m2 );
        }
        else if ( m2 == 0 && std::abs( m1 ) <=1 ){
                          cg = cg2( x1 - y2 + y3, x2 - 1, x1 + x3 - 2, x3 - y1, j1, j3, j3, m1 );
        }
        else if ( m1 == 0 && std::abs( m3 ) <= 1 ){
                          cg = cg2( x1, x1 - 1, x2 + x3 - 2, x2 - y3, j2, j3, j3, -m3 );
        }
        else              cg = cg3( x1, x2, x3, y1, y2, y3 );
    }

    return( cg );
}

Here is the call graph for this function:

Here is the caller graph for this function:

double nf_amc_factorial

(

int

)

Definition at line 96 of file nf_angularMomentumCoupling.cc.

                                  {
/*
*       returns n! for pre-computed table. INFINITY is return if n is negative or too large.
*/
    return G4Exp( nf_amc_log_factorial( n ) );
}

Here is the call graph for this function:

double nf_amc_log_factorial

(

int

)

Definition at line 85 of file nf_angularMomentumCoupling.cc.

                                      {
/*
*       returns ln( n! ).
*/
    if( n > MAX_FACTORIAL ) return( INFINITY );
    if( n < 0 ) return( INFINITY );
    return nf_amc_log_fact[n];
}

Here is the caller graph for this function:

double nf_amc_racah	(	int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 253 of file nf_angularMomentumCoupling.cc.

                                                                      {
/*
*       Racah coefficient definition in Edmonds (AR Edmonds, "Angular Momentum in Quantum Mechanics", Princeton (1980) is
*       W(j1, j2, l2, l1 ; j3, l3) = (-1)^(j1+j2+l1+l2) * { j1 j2 j3 }
*                                                         { l1 l2 l3 }
*       The call signature of W(...) appears jumbled, but hey, that's the convention.
*
*       This convention is exactly that used by Blatt-Biedenharn (Rev. Mod. Phys. 24, 258 (1952)) too
*/

    double sig;

    sig = ( ( ( j1 + j2 + l1 + l2 ) % 4 == 0 ) ?  1.0 : -1.0 );
    return sig * nf_amc_wigner_6j( j1, j2, j3, l1, l2, l3 );
}

Here is the call graph for this function:

Here is the caller graph for this function:

double nf_amc_reduced_matrix_element	(	int	,
		int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 473 of file nf_angularMomentumCoupling.cc.

                                                                                               {
/*
*       Reduced Matrix Element for Tensor Operator
*           = < l1j1 || T(YL,sigma_S)J || l0j0 >
*
*   M.B.Johnson, L.W.Owen, G.R.Satchler
*   Phys. Rev. 142, 748 (1966)
*   Note: definition differs from JOS by the factor sqrt(2j1+1)
*/
    int    llt;
    double x1, x2, x3, reduced_mat, clebsh_gordan;

    if ( parity( lt ) != parity( l0 ) * parity( l1 ) ) return( 0.0 );
    if ( std::abs( l0 - l1 ) > lt || ( l0 + l1 ) < lt ) return( 0.0 );
    if ( std::abs( ( j0 - j1 ) / 2 ) > jt || ( ( j0 + j1 ) / 2 ) < jt ) return( 0.0 );

    llt = 2 * lt;
    jt *= 2;
    st *= 2;

    if( ( clebsh_gordan = nf_amc_clebsh_gordan( j1, j0, 1, -1, jt ) ) == INFINITY ) return( INFINITY );

    reduced_mat = 1.0 / std::sqrt( 4 * M_PI ) * clebsh_gordan / std::sqrt( jt + 1.0 )         /* BRB jt + 1 <= 0? */
                * std::sqrt( ( j0 + 1.0 ) * ( j1 + 1.0 ) * ( llt + 1.0 ) )
                * parity( ( j1 - j0 ) / 2 ) * parity( ( -l0 + l1 + lt ) / 2 ) * parity( ( j0 - 1 ) / 2 );

    if( st == 2 ){
        x1 = ( l0 - j0 / 2.0 ) * ( j0 + 1.0 );
        x2 = ( l1 - j1 / 2.0 ) * ( j1 + 1.0 );
        if ( jt == llt ){
            x3 = ( lt == 0 ) ? 0 :  ( x1 - x2 ) / std::sqrt( lt * ( lt + 1.0 ) );
        }
        else if ( jt == ( llt - st ) ){
            x3 = ( lt == 0 ) ? 0 : -( lt + x1 + x2 ) / std::sqrt( lt * ( 2.0 * lt + 1.0 ) );
        }
        else if ( jt == ( llt + st ) ){
            x3 = ( lt + 1 - x1 - x2 ) / std::sqrt( ( 2.0 * lt + 1.0 ) * ( lt + 1.0 ) );
        }
        else{
            x3 = 1.0;
        }
    }
    else x3 = 1.0;
    reduced_mat *= x3;

    return( reduced_mat );
}

Here is the call graph for this function:

double nf_amc_wigner_3j	(	int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 105 of file nf_angularMomentumCoupling.cc.

                                                                          {
/*
*       Wigner's 3J symbol (similar to Clebsh-Gordan)
*           = / j1 j2 j3 \
*             \ j4 j5 j6 /
*/
    double cg;

    if( ( j4 + j5 + j6 ) != 0 ) return( 0.0 );
    if( ( cg = nf_amc_clebsh_gordan( j1, j2, j4, j5, j3 ) ) == 0.0 ) return ( 0.0 );
    if( cg == INFINITY ) return( cg );
    return( ( ( ( j1 - j2 - j6 ) % 4 == 0 ) ?  1.0 : -1.0 ) * cg / std::sqrt( j3 + 1.0 ) );          /* BRB j3 + 1 <= 0? */
}

Here is the call graph for this function:

double nf_amc_wigner_6j	(	int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 121 of file nf_angularMomentumCoupling.cc.

                                                                          {
/*
*       Wigner's 6J symbol (similar to Racah)
*               = { j1 j2 j3 }
*                 { j4 j5 j6 }
*/
    int i, x[6];

    x[0] = j1; x[1] = j2; x[2] = j3; x[3] = j4; x[4] = j5; x[5] = j6;
    for( i = 0; i < 6; i++ ) if ( x[i] == 0 ) return( w6j0( i, x ) );

    return( w6j1( x ) );
}

Here is the call graph for this function:

Here is the caller graph for this function:

double nf_amc_wigner_9j	(	int	,
		int	,
		int	,
		int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

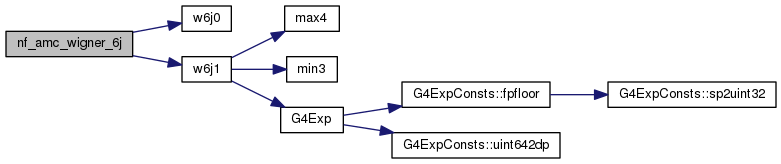
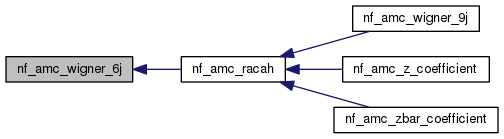
Definition at line 226 of file nf_angularMomentumCoupling.cc.

                                                                                                  {
/*
*       Wigner's 9J symbol
*             / j1 j2 j3 \
*           = | j4 j5 j6 |
*             \ j7 j8 j9 /
*
*/
    int i, i0, i1;
    double rac;

    i0 = max3( std::abs( j1 - j9 ), std::abs( j2 - j6 ), std::abs( j4 - j8 ) );
    i1 = min3(     ( j1 + j9 ),     ( j2 + j6 ),     ( j4 + j8 ) );

    rac = 0.0;
    for ( i = i0; i <= i1; i += 2 ){ 
        rac += nf_amc_racah( j1, j4, j9, j8, j7,  i )
            *  nf_amc_racah( j2, j5,  i, j4, j8, j6 )
            *  nf_amc_racah( j9,  i, j3, j2, j1, j6 ) * ( i + 1 );
        if( rac == INFINITY ) return( INFINITY );
    }

    return( ( ( (int)( ( j1 + j3 + j5 + j8 ) / 2 + j2 + j4 + j9 ) % 4 == 0 ) ?  1.0 : -1.0 ) * rac );
}

Here is the call graph for this function:

double nf_amc_z_coefficient	(	int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 437 of file nf_angularMomentumCoupling.cc.

                                                                             {
/*
*       Biedenharn's Z-coefficient coefficient
*           =  Z(l1  j1  l2  j2 | S L )
*/
    double z, clebsh_gordan = nf_amc_clebsh_gordan( l1, l2, 0, 0, ll ), racah = nf_amc_racah( l1, j1, l2, j2, s, ll );

    if( ( clebsh_gordan == INFINITY ) || ( racah == INFINITY ) ) return( INFINITY );
    z = ( ( ( -l1 + l2 + ll ) % 8 == 0 ) ? 1.0 : -1.0 )
        * std::sqrt( l1 + 1.0 ) * std::sqrt( l2 + 1.0 ) * std::sqrt( j1 + 1.0 ) * std::sqrt( j2 + 1.0 ) * clebsh_gordan * racah;

   return( z );
}

Here is the call graph for this function:

double nf_amc_zbar_coefficient	(	int	,
		int	,
		int	,
		int	,
		int	,
		int
	)

Definition at line 453 of file nf_angularMomentumCoupling.cc.

                                                                                {
/*
*       Lane & Thomas's Zbar-coefficient coefficient
*           = Zbar(l1  j1  l2  j2 | S L )
*           = (-i)^( -l1 + l2 + ll ) * Z(l1  j1  l2  j2 | S L )
*
*       Lane & Thomas Rev. Mod. Phys. 30, 257-353 (1958).
*       Note, Lane & Thomas define this because they did not like the different phase convention in Blatt & Biedenharn's Z coefficient.  They changed it to get better time-reversal behavior.
*       Froehner uses Lane & Thomas convention as does T. Kawano.
*/
    double zbar, clebsh_gordan = nf_amc_clebsh_gordan( l1, l2, 0, 0, ll ), racah = nf_amc_racah( l1, j1, l2, j2, s, ll );

    if( ( clebsh_gordan == INFINITY ) || ( racah == INFINITY ) ) return( INFINITY );
    zbar = std::sqrt( l1 + 1.0 ) * std::sqrt( l2 + 1.0 ) * std::sqrt( j1 + 1.0 ) * std::sqrt( j2 + 1.0 ) * clebsh_gordan * racah;

   return( zbar );
}

Here is the call graph for this function:

double nf_exponentialIntegral	(	int	n,
		double	x,
		nfu_status *	status
	)

Definition at line 28 of file nf_exponentialIntegral.cc.

                                                                     {

    int i, ii, nm1;
    double a, b, c, d, del, fact, h, psi;
    double ans = 0.0;

    *status = nfu_badInput;
    if( !isfinite( x ) ) return( x );
    *status = nfu_Okay;

    nm1 = n - 1;
    if( ( n < 0 ) || ( x < 0.0 ) || ( ( x == 0.0 ) && ( ( n == 0 ) || ( n == 1 ) ) ) ) {
        *status = nfu_badInput; }
    else {
        if( n == 0 ) {
            ans = G4Exp( -x ) / x; }                  /* Special case */
        else if( x == 0.0 ) {
            ans = 1.0 / nm1; }                      /* Another special case */
        else if( x > 1.0 ) {                        /* Lentz's algorithm */
            b = x + n;
            c = 1.0 / FPMIN;
            d = 1.0 / b;
            h = d;
            for( i = 1; i <= MAXIT; i++ ) {
                a = -i * ( nm1 + i );
                b += 2.0;
                d = 1.0 / ( a * d + b );            /* Denominators cannot be zero */
                c = b + a / c;
                del = c * d;
                h *= del;
                if( fabs( del - 1.0 ) < EPS ) return( h * G4Exp( -x ) );
            }
            *status = nfu_failedToConverge; }
        else {
            ans = ( nm1 != 0 ) ? 1.0 / nm1 : -G4Log(x) - EULER;   /* Set first term */
            fact = 1.0;
            for( i = 1; i <= MAXIT; i++ ) {
                fact *= -x / i;
                if( i != nm1 ) {
                    del = -fact / ( i - nm1 ); }
                else {
                    psi = -EULER;                   /* Compute psi(n) */
                    for( ii = 1; ii <= nm1; ii++ ) psi += 1.0 / ii;
                    del = fact * ( -G4Log( x ) + psi );
                }
                ans += del;
                if( fabs( del ) < fabs( ans ) * EPS ) return( ans );
            }
            *status = nfu_failedToConverge;
        }
    }
    return( ans );
}

Here is the call graph for this function:

Here is the caller graph for this function:

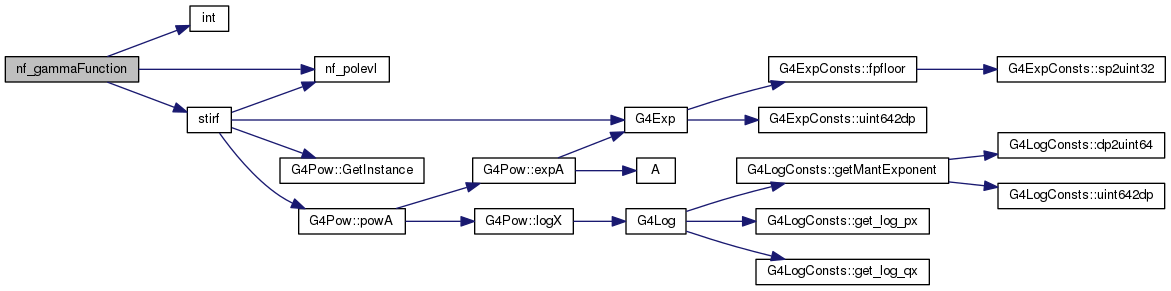
double nf_gammaFunction	(	double	x,
		nfu_status *	status
	)

Definition at line 126 of file nf_gammaFunctions.cc.

                                                        {

    double p, q, z;
    int i, sgngam = 1;

    *status = nfu_badInput;
    if( !isfinite( x ) ) return( x );
    *status = nfu_Okay;

    q = fabs( x );

    if( q > 33.0 ) {
        if( x < 0.0 ) {
            p = floor( q );
            if( p == q ) goto goverf;
            i = (int) p;
            if( ( i & 1 ) == 0 ) sgngam = -1;
            z = q - p;
            if( z > 0.5 ) {
                p += 1.0;
                z = q - p;
            }
            z = q * sin( M_PI * z );
            if( z == 0.0 ) goto goverf;
            z = M_PI / ( fabs( z ) * stirf( q, status ) );
        }
        else {
            z = stirf( x, status );
        }
        return( sgngam * z );
    }

    z = 1.0;
    while( x >= 3.0 ) {
        x -= 1.0;
        z *= x;
    } // Loop checking, 11.06.2015, T. Koi

    while( x < 0.0 ) {
        if( x > -1.E-9 ) goto small;
        z /= x;
        x += 1.0;
    } // Loop checking, 11.06.2015, T. Koi

    while( x < 2.0 ) {
        if( x < 1.e-9 ) goto small;
        z /= x;
        x += 1.0;
    } // Loop checking, 11.06.2015, T. Koi

    if( x == 2.0 ) return( z );

    x -= 2.0;
    p = nf_polevl( x, P, 6 );
    q = nf_polevl( x, Q, 7 );
    return( z * p / q );

small:
    if( x == 0.0 ) goto goverf;
    return( z / ( ( 1.0 + 0.5772156649015329 * x ) * x ) );

goverf:
    return( sgngam * DBL_MAX );
}

Here is the call graph for this function:

Here is the caller graph for this function:

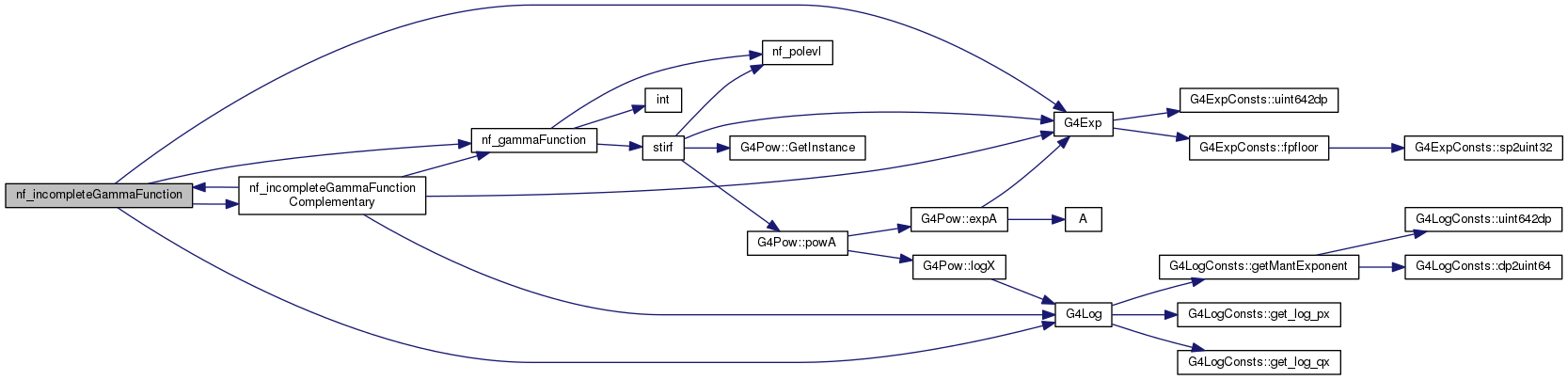
double nf_incompleteGammaFunction	(	double	a,
		double	x,
		nfu_status *	status
	)

Definition at line 155 of file nf_incompleteGammaFunctions.cc.

                                                                            {
/* left tail of incomplete gamma function:
*
*          inf.      k
*   a  -x   -       x
*  x  e     >   ----------
*           -     -
*          k=0   | (a+k+1)
*/
    double ans, ax, c, r;

    *status = nfu_badInput;
    if( !isfinite( x ) ) return( x );
    *status = nfu_Okay;

    if( ( x <= 0 ) || ( a <= 0 ) ) return( 0.0 );
    if( ( x > 1.0 ) && ( x > a ) ) return( nf_gammaFunction( a, status ) - nf_incompleteGammaFunctionComplementary( a, x, status ) );

    ax = G4Exp( a * G4Log( x ) - x );       /* Compute  x**a * exp(-x) */
    if( ax == 0. ) return( 0.0 );

    r = a;                                                      /* power series */
    c = 1.0;
    ans = 1.0;
    do {
        r += 1.0;
        c *= x / r;
        ans += c;
    } while( c > ans * DBL_EPSILON ); // Loop checking, 11.06.2015, T. Koi

    return( ans * ax / a );
}

Here is the call graph for this function:

Here is the caller graph for this function:

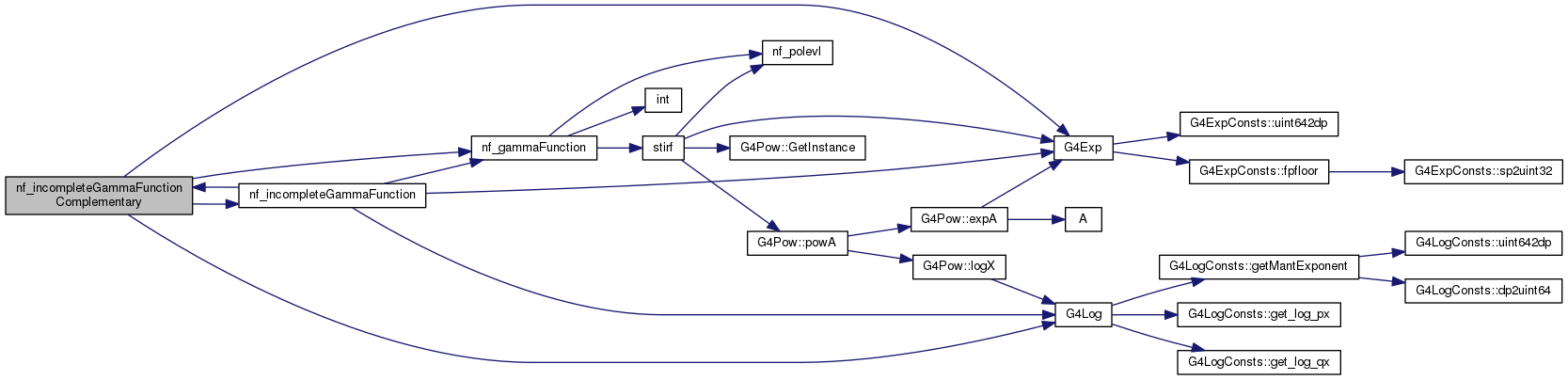
double nf_incompleteGammaFunctionComplementary	(	double	a,
		double	x,
		nfu_status *	status
	)

Definition at line 88 of file nf_incompleteGammaFunctions.cc.

                                                                                         {

    double ans, ax, c, yc, r, t, y, z;
    double pk, pkm1, pkm2, qk, qkm1, qkm2;

    *status = nfu_badInput;
    if( !isfinite( x ) ) return( x );
    *status = nfu_Okay;

    if( ( x <= 0 ) || ( a <= 0 ) ) return( 1.0 );
    if( ( x < 1.0 ) || ( x < a ) ) return( nf_gammaFunction( a, status ) - nf_incompleteGammaFunction( a, x, status ) );

    ax = G4Exp( a * G4Log( x ) - x );
    if( ax == 0. ) return( 0.0 );

    if( x < 10000. ) {
        y = 1.0 - a;                        /* continued fraction */
        z = x + y + 1.0;
        c = 0.0;
        pkm2 = 1.0;
        qkm2 = x;
        pkm1 = x + 1.0;
        qkm1 = z * x;
        ans = pkm1 / qkm1;

        do {
            c += 1.0;
            y += 1.0;
            z += 2.0;
            yc = y * c;
            pk = pkm1 * z  -  pkm2 * yc;
            qk = qkm1 * z  -  qkm2 * yc;
            if( qk != 0 ) {
                r = pk / qk;
                t = fabs( ( ans - r ) / r );
                ans = r; }
            else {
                t = 1.0;
            }
            pkm2 = pkm1;
            pkm1 = pk;
            qkm2 = qkm1;
            qkm1 = qk;
            if( fabs( pk ) > big ) {
                pkm2 *= biginv;
                pkm1 *= biginv;
                qkm2 *= biginv;
                qkm1 *= biginv;
            }
        } while( t > DBL_EPSILON ); } // Loop checking, 11.06.2015, T. Koi
    else {                                  /* Asymptotic expansion. */
        y = 1. / x;
        r = a;
        c = 1.;
        ans = 1.;
        do {
            a -= 1.;
            c *= a * y;
            ans += c;
        } while( fabs( c ) > 100 * ans * DBL_EPSILON ); // Loop checking, 11.06.2015, T. Koi
    }

    return( ans * ax );
}

Here is the call graph for this function:

Here is the caller graph for this function:

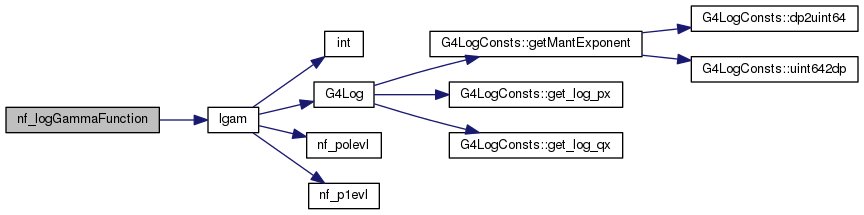
double nf_logGammaFunction	(	double	x,
		nfu_status *	status
	)

Definition at line 206 of file nf_gammaFunctions.cc.

                                                           {
/* Logarithm of gamma function */

    int sgngam;

    *status = nfu_badInput;
    if( !isfinite( x ) ) return( x );
    *status = nfu_Okay;
    return( lgam( x, &sgngam, status ) );
}

Here is the call graph for this function:

double nf_p1evl	(	double	x,
		double	coef[],
		int	N
	)

Definition at line 67 of file nf_polevl.cc.

                                                  {

    double ans;
    double *p;
    int i;

    p = coef;
    ans = x + *p++;
    i = N-1;

    do {
        ans = ans * x + *p++; }
    while( --i ); // Loop checking, 11.06.2015, T. Koi

    return( ans );
}

Here is the caller graph for this function:

double nf_polevl	(	double	x,
		double	coef[],
		int	N
	)

Definition at line 46 of file nf_polevl.cc.

                                                   {

    double ans;
    int i;
    double *p;

    p = coef;
    ans = *p++;
    i = N;

    do {
        ans = ans * x  +  *p++; }
    while( --i ); // Loop checking, 11.06.2015, T. Koi

    return( ans );
}

Here is the caller graph for this function: