|
Geant4
10.03.p03
|
|
Geant4
10.03.p03
|
#include "nf_Legendre.h"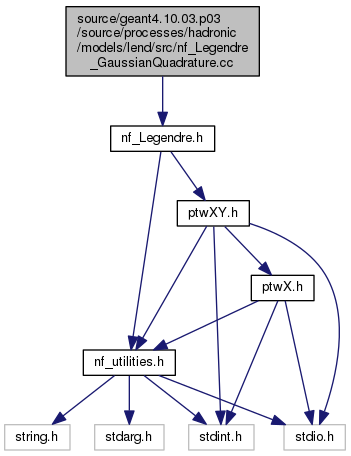
Go to the source code of this file.
Classes | |
| struct | nf_Legendre_GaussianQuadrature_degree |
Macros | |
| #define | n_3 3 |
| #define | n_4 4 |
| #define | n_5 5 |
| #define | n_10 10 |
| #define | n_20 20 |
| #define | n_40 40 |
| #define | nSets 6 |
Functions | |
| nfu_status | nf_Legendre_GaussianQuadrature (int degree, double x1, double x2, nf_Legendre_GaussianQuadrature_callback func, void *argList, double *integral) |
Variables | |
| static double | sqrt_inv3 = 0.57735026918962576451 |
| static double | weights_3 [(n_3+1)/2] = { 8. / 9., 5. / 9. } |
| static double | xis_3 [(n_3+1)/2] = { 0., 0.77459666924148337704 } |
| static double | weights_4 [(n_4+1)/2] = { 0.65214515486254614263, 0.34785484513745385737 } |
| static double | xis_4 [(n_4+1)/2] = { 0.33998104358485626480, 0.86113631159405257522 } |
| static double | weights_5 [(n_5+1)/2] = { 0.568888888888889, 0.478628670499366, 0.236926885056189 } |
| static double | xis_5 [(n_5+1)/2] = { 0.0, 0.538469310105683, 0.906179845938664 } |
| static double | weights_10 [(n_10+1)/2] = { 0.295524224714752870, 0.269266719309996355, 0.219086362515982044, 0.149451349150580593, 0.066671344308688138 } |
| static double | xis_10 [(n_10+1)/2] = { 0.148874338981631211, 0.433395394129247191, 0.679409568299024406, 0.865063366688984511, 0.973906528517171720 } |
| static double | weights_20 [(n_20+1)/2] |
| static double | xis_20 [(n_20+1)/2] |
| static double | weights_40 [(n_40+1)/2] |
| static double | xis_40 [(n_40+1)/2] |
| static struct nf_Legendre_GaussianQuadrature_degree | GaussianQuadrature_degrees [nSets] |
| #define n_10 10 |
Definition at line 33 of file nf_Legendre_GaussianQuadrature.cc.
| #define n_20 20 |
Definition at line 37 of file nf_Legendre_GaussianQuadrature.cc.
| #define n_3 3 |
Definition at line 21 of file nf_Legendre_GaussianQuadrature.cc.
| #define n_4 4 |
Definition at line 25 of file nf_Legendre_GaussianQuadrature.cc.
| #define n_40 40 |
Definition at line 45 of file nf_Legendre_GaussianQuadrature.cc.
| #define n_5 5 |
Definition at line 29 of file nf_Legendre_GaussianQuadrature.cc.
| #define nSets 6 |
Definition at line 57 of file nf_Legendre_GaussianQuadrature.cc.
| nfu_status nf_Legendre_GaussianQuadrature | ( | int | degree, |
| double | x1, | ||
| double | x2, | ||
| nf_Legendre_GaussianQuadrature_callback | func, | ||
| void * | argList, | ||
| double * | integral | ||
| ) |
Definition at line 63 of file nf_Legendre_GaussianQuadrature.cc.

|
static |
Definition at line 58 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 19 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 34 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 38 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 22 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 26 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 46 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 30 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 35 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 41 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 23 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 27 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 51 of file nf_Legendre_GaussianQuadrature.cc.
|
static |
Definition at line 31 of file nf_Legendre_GaussianQuadrature.cc.