269 if (
true)
return bbox.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
271 if (bbox.BoundingBoxVsVoxelLimits(pAxis,pVoxelLimit,pTransform,pMin,pMax))
273 return exist = (pMin < pMax) ?
true :
false;
284 const G4int NSTEPS = 24;
289 G4double sinHalf = std::sin(0.5*ang);
290 G4double cosHalf = std::cos(0.5*ang);
291 G4double sinStep = 2.*sinHalf*cosHalf;
292 G4double cosStep = 1. - 2.*sinHalf*sinHalf;
297 if (rmin == 0 && dphi ==
twopi)
303 for (
G4int k=0; k<NSTEPS; ++k)
305 baseA[k].set(rext*cosCur,rext*sinCur,-dz);
306 baseB[k].set(rext*cosCur,rext*sinCur, dz);
309 sinCur = sinCur*cosStep + cosCur*sinStep;
310 cosCur = cosCur*cosStep - sinTmp*sinStep;
312 std::vector<const G4ThreeVectorList *> polygons(2);
313 polygons[0] = &baseA;
314 polygons[1] = &baseB;
316 exist = benv.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
324 G4double sinCur = sinStart*cosHalf + cosStart*sinHalf;
325 G4double cosCur = cosStart*cosHalf - sinStart*sinHalf;
329 for (
G4int k=0; k<ksteps+2; ++k) pols[k].resize(4);
330 pols[0][0].set(rmin*cosStart,rmin*sinStart, dz);
331 pols[0][1].set(rmin*cosStart,rmin*sinStart,-dz);
332 pols[0][2].set(rmax*cosStart,rmax*sinStart,-dz);
333 pols[0][3].set(rmax*cosStart,rmax*sinStart, dz);
334 for (
G4int k=1; k<ksteps+1; ++k)
336 pols[k][0].set(rmin*cosCur,rmin*sinCur, dz);
337 pols[k][1].set(rmin*cosCur,rmin*sinCur,-dz);
338 pols[k][2].set(rext*cosCur,rext*sinCur,-dz);
339 pols[k][3].set(rext*cosCur,rext*sinCur, dz);
342 sinCur = sinCur*cosStep + cosCur*sinStep;
343 cosCur = cosCur*cosStep - sinTmp*sinStep;
345 pols[ksteps+1][0].set(rmin*cosEnd,rmin*sinEnd, dz);
346 pols[ksteps+1][1].set(rmin*cosEnd,rmin*sinEnd,-dz);
347 pols[ksteps+1][2].set(rmax*cosEnd,rmax*sinEnd,-dz);
348 pols[ksteps+1][3].set(rmax*cosEnd,rmax*sinEnd, dz);
351 std::vector<const G4ThreeVectorList *> polygons;
352 polygons.resize(ksteps+2);
353 for (
G4int k=0; k<ksteps+2; ++k) polygons[k] = &pols[k];
355 exist = benv.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
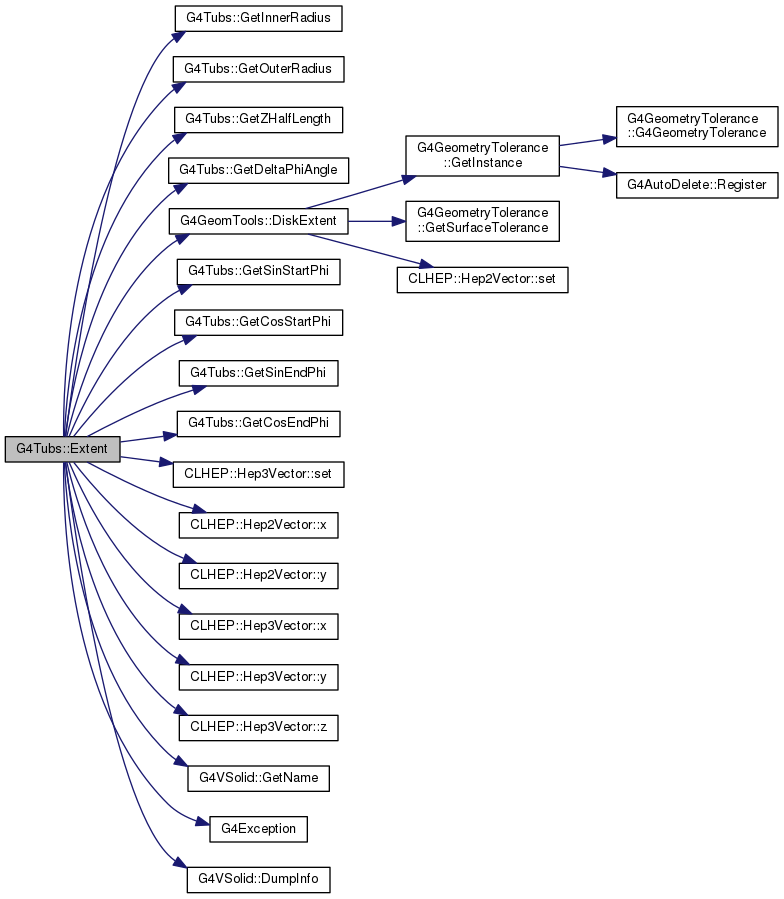
void Extent(G4ThreeVector &pMin, G4ThreeVector &pMax) const
G4double GetCosEndPhi() const
static constexpr double twopi
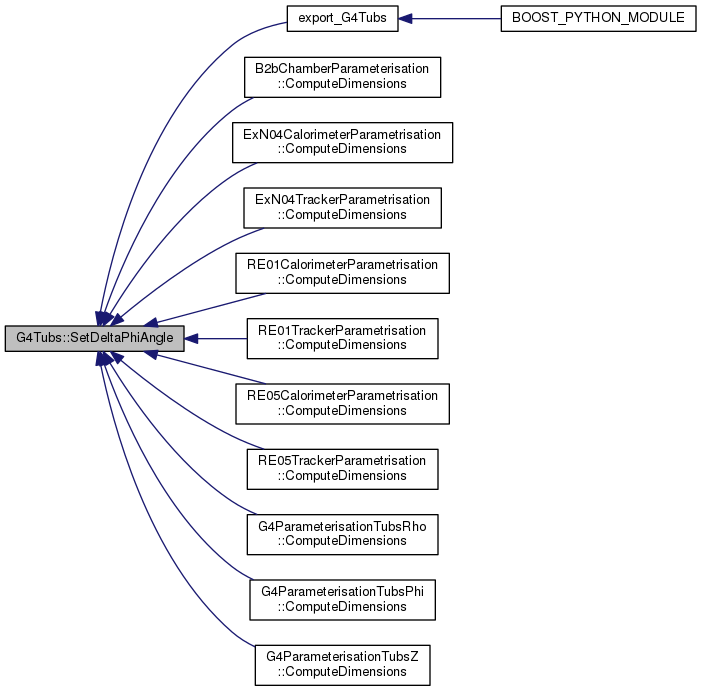
G4double GetDeltaPhiAngle() const
G4double GetSinEndPhi() const
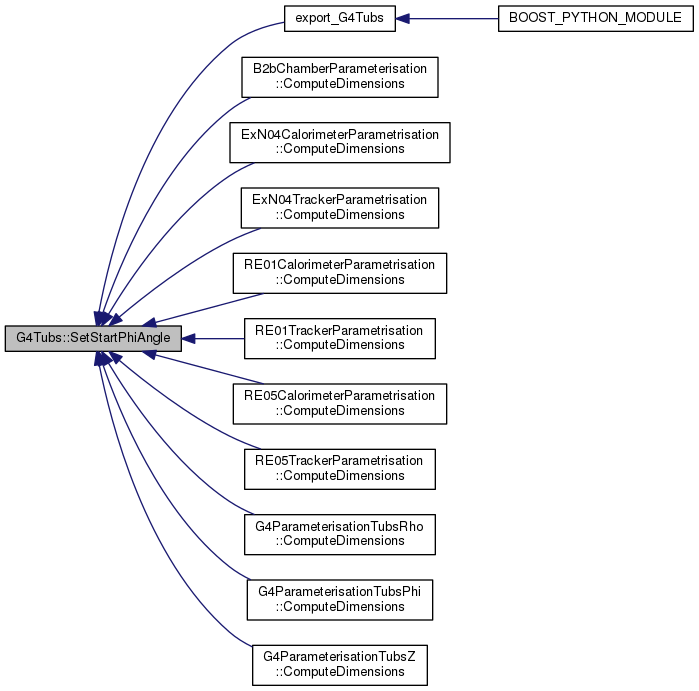
G4double GetSinStartPhi() const
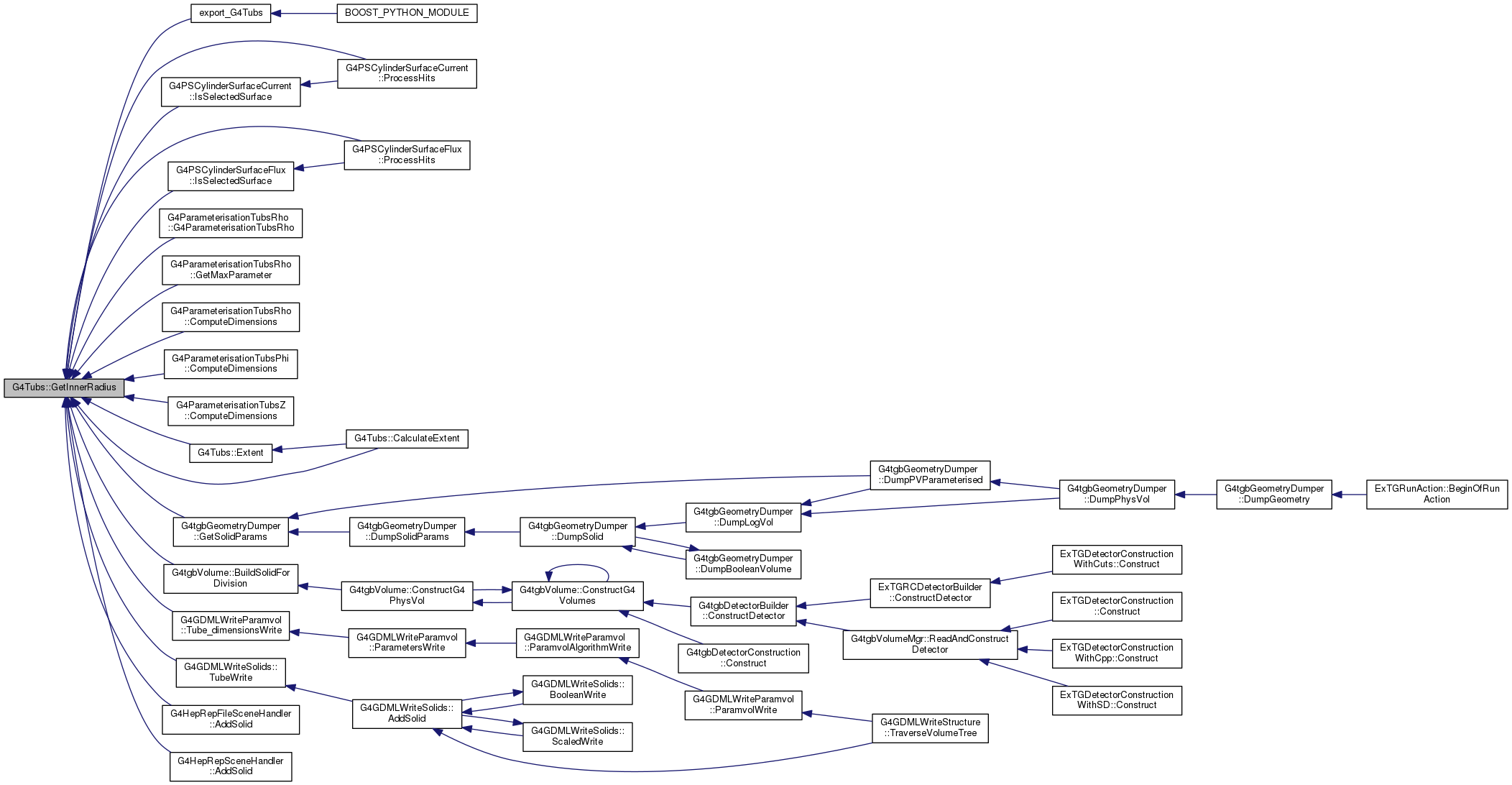
G4double GetInnerRadius() const
std::vector< G4ThreeVector > G4ThreeVectorList
G4double GetZHalfLength() const
static constexpr double deg
G4double GetCosStartPhi() const
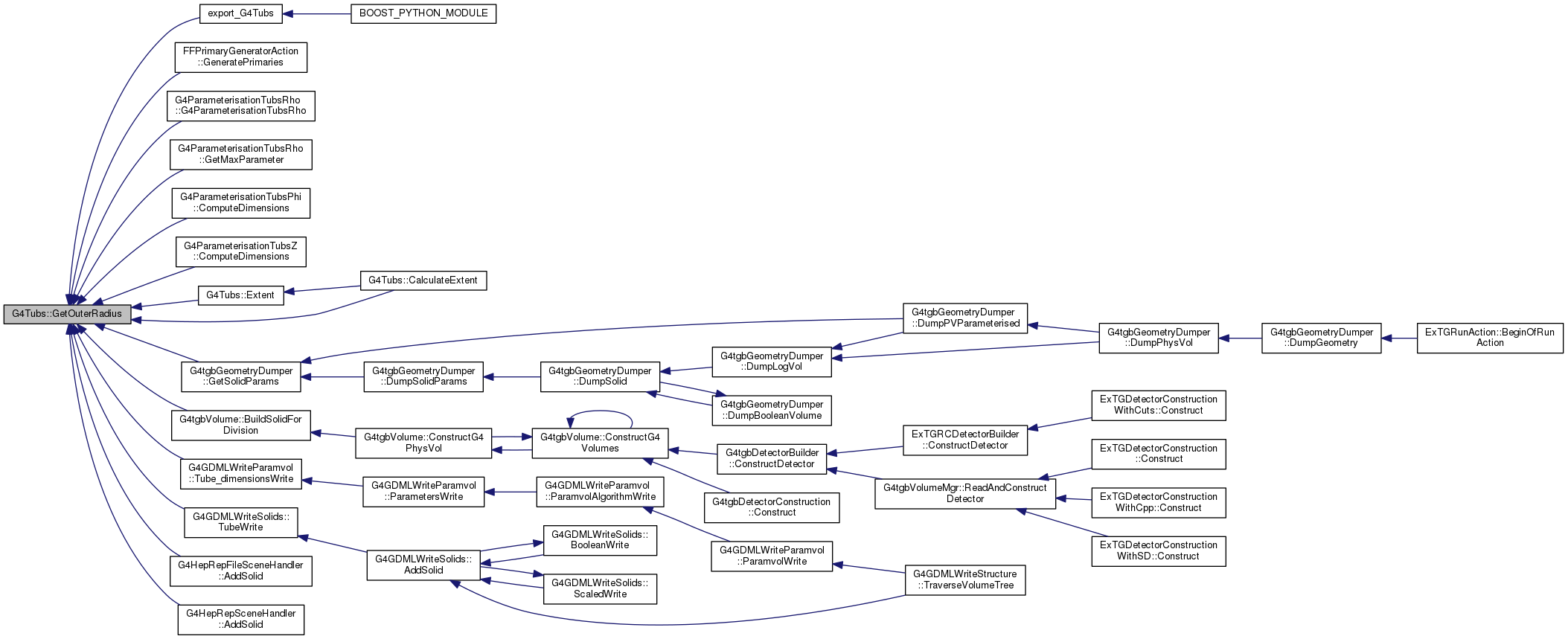
G4double GetOuterRadius() const
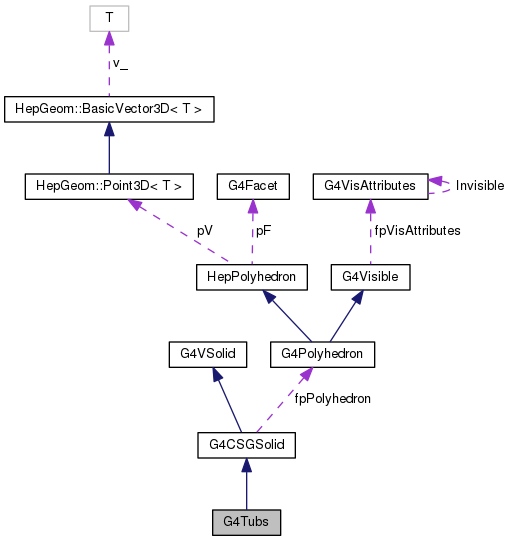
 Protected Member Functions inherited from G4CSGSolid
Protected Member Functions inherited from G4CSGSolid Protected Member Functions inherited from G4VSolid
Protected Member Functions inherited from G4VSolid Protected Attributes inherited from G4CSGSolid
Protected Attributes inherited from G4CSGSolid Protected Attributes inherited from G4VSolid
Protected Attributes inherited from G4VSolid