Geant4  10.03.p03
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Public Member Functions | List of all members
G4Sphere Class Reference

#include <G4Sphere.hh>

Inheritance diagram for G4Sphere:
Inheritance graph
[legend]
Collaboration diagram for G4Sphere:
Collaboration graph
[legend]

Public Member Functions

 G4Sphere (const G4String &pName, G4double pRmin, G4double pRmax, G4double pSPhi, G4double pDPhi, G4double pSTheta, G4double pDTheta)
 
 ~G4Sphere ()
 
G4double GetInnerRadius () const
 
G4double GetOuterRadius () const
 
G4double GetStartPhiAngle () const
 
G4double GetDeltaPhiAngle () const
 
G4double GetStartThetaAngle () const
 
G4double GetDeltaThetaAngle () const
 
G4double GetSinStartPhi () const
 
G4double GetCosStartPhi () const
 
G4double GetSinEndPhi () const
 
G4double GetCosEndPhi () const
 
G4double GetSinStartTheta () const
 
G4double GetCosStartTheta () const
 
G4double GetSinEndTheta () const
 
G4double GetCosEndTheta () const
 
void SetInnerRadius (G4double newRMin)
 
void SetOuterRadius (G4double newRmax)
 
void SetStartPhiAngle (G4double newSphi, G4bool trig=true)
 
void SetDeltaPhiAngle (G4double newDphi)
 
void SetStartThetaAngle (G4double newSTheta)
 
void SetDeltaThetaAngle (G4double newDTheta)
 
G4double GetCubicVolume ()
 
G4double GetSurfaceArea ()
 
void ComputeDimensions (G4VPVParameterisation *p, const G4int n, const G4VPhysicalVolume *pRep)
 
void Extent (G4ThreeVector &pMin, G4ThreeVector &pMax) const
 
G4bool CalculateExtent (const EAxis pAxis, const G4VoxelLimits &pVoxelLimit, const G4AffineTransform &pTransform, G4double &pmin, G4double &pmax) const
 
EInside Inside (const G4ThreeVector &p) const
 
G4ThreeVector SurfaceNormal (const G4ThreeVector &p) const
 
G4double DistanceToIn (const G4ThreeVector &p, const G4ThreeVector &v) const
 
G4double DistanceToIn (const G4ThreeVector &p) const
 
G4double DistanceToOut (const G4ThreeVector &p, const G4ThreeVector &v, const G4bool calcNorm=G4bool(false), G4bool *validNorm=0, G4ThreeVector *n=0) const
 
G4double DistanceToOut (const G4ThreeVector &p) const
 
G4GeometryType GetEntityType () const
 
G4ThreeVector GetPointOnSurface () const
 
G4VSolid * Clone () const
 
std::ostream & StreamInfo (std::ostream &os) const
 
G4VisExtent GetExtent () const
 
void DescribeYourselfTo (G4VGraphicsScene &scene) const
 
G4Polyhedron * CreatePolyhedron () const
 
 G4Sphere (__void__ &)
 
 G4Sphere (const G4Sphere &rhs)
 
G4Sphere & operator= (const G4Sphere &rhs)
 
G4double GetRmin () const
 
G4double GetRmax () const
 
G4double GetSPhi () const
 
G4double GetDPhi () const
 
G4double GetSTheta () const
 
G4double GetDTheta () const
 
G4double GetInsideRadius () const
 
void SetInsideRadius (G4double newRmin)
 
- Public Member Functions inherited from G4CSGSolid
 G4CSGSolid (const G4String &pName)
 
virtual ~G4CSGSolid ()
 
virtual G4Polyhedron * GetPolyhedron () const
 
 G4CSGSolid (__void__ &)
 
 G4CSGSolid (const G4CSGSolid &rhs)
 
G4CSGSolid & operator= (const G4CSGSolid &rhs)
 
- Public Member Functions inherited from G4VSolid
 G4VSolid (const G4String &name)
 
virtual ~G4VSolid ()
 
G4bool operator== (const G4VSolid &s) const
 
G4String GetName () const
 
void SetName (const G4String &name)
 
G4double GetTolerance () const
 
void DumpInfo () const
 
virtual const G4VSolid * GetConstituentSolid (G4int no) const
 
virtual G4VSolid * GetConstituentSolid (G4int no)
 
virtual const G4DisplacedSolid * GetDisplacedSolidPtr () const
 
virtual G4DisplacedSolid * GetDisplacedSolidPtr ()
 
 G4VSolid (__void__ &)
 
 G4VSolid (const G4VSolid &rhs)
 
G4VSolid & operator= (const G4VSolid &rhs)
 
G4double EstimateCubicVolume (G4int nStat, G4double epsilon) const
 
G4double EstimateSurfaceArea (G4int nStat, G4double ell) const
 

Additional Inherited Members

- Protected Member Functions inherited from G4CSGSolid
G4double GetRadiusInRing (G4double rmin, G4double rmax) const
 
- Protected Member Functions inherited from G4VSolid
void CalculateClippedPolygonExtent (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
 
void ClipCrossSection (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
 
void ClipBetweenSections (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
 
void ClipPolygon (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis) const
 
- Protected Attributes inherited from G4CSGSolid
G4double fCubicVolume
 
G4double fSurfaceArea
 
G4bool fRebuildPolyhedron
 
G4Polyhedron * fpPolyhedron
 
- Protected Attributes inherited from G4VSolid
G4double kCarTolerance
 

Detailed Description

Definition at line 87 of file G4Sphere.hh.

Constructor & Destructor Documentation

G4Sphere::G4Sphere ( const G4String &  pName,
G4double  pRmin,
G4double  pRmax,
G4double  pSPhi,
G4double  pDPhi,
G4double  pSTheta,
G4double  pDTheta 
)

Definition at line 95 of file G4Sphere.cc.

99  : G4CSGSolid(pName), fEpsilon(2.e-11), fSPhi(0.0),
100  fFullPhiSphere(true), fFullThetaSphere(true)
101 {
102  kAngTolerance = G4GeometryTolerance::GetInstance()->GetAngularTolerance();
103  kRadTolerance = G4GeometryTolerance::GetInstance()->GetRadialTolerance();
104 
105  halfCarTolerance = 0.5*kCarTolerance;
106  halfAngTolerance = 0.5*kAngTolerance;
107 
108  // Check radii and set radial tolerances
109 
110  if ( (pRmin >= pRmax) || (pRmax < 1.1*kRadTolerance) || (pRmin < 0) )
111  {
112  std::ostringstream message;
113  message << "Invalid radii for Solid: " << GetName() << G4endl
114  << " pRmin = " << pRmin << ", pRmax = " << pRmax;
115  G4Exception("G4Sphere::G4Sphere()", "GeomSolids0002",
116  FatalException, message);
117  }
118  fRmin=pRmin; fRmax=pRmax;
119  fRminTolerance = (fRmin) ? std::max( kRadTolerance, fEpsilon*fRmin ) : 0;
120  fRmaxTolerance = std::max( kRadTolerance, fEpsilon*fRmax );
121 
122  // Check angles
123 
124  CheckPhiAngles(pSPhi, pDPhi);
125  CheckThetaAngles(pSTheta, pDTheta);
126 }
G4VSolid::GetName
G4String GetName() const
G4GeometryTolerance::GetRadialTolerance
G4double GetRadialTolerance() const
Definition: G4GeometryTolerance.cc:97
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
G4CSGSolid::G4CSGSolid
G4CSGSolid(const G4String &pName)
Definition: G4CSGSolid.cc:49
G4INCL::Math::max
T max(const T t1, const T t2)
brief Return the largest of the two arguments
Definition: G4INCLGlobals.hh:112
FatalException
Definition: G4ExceptionSeverity.hh:60
G4endl
#define G4endl
Definition: G4ios.hh:61
G4VSolid::kCarTolerance
G4double kCarTolerance
Definition: G4VSolid.hh:307
G4GeometryTolerance::GetAngularTolerance
G4double GetAngularTolerance() const
Definition: G4GeometryTolerance.cc:92
G4GeometryTolerance::GetInstance
static G4GeometryTolerance * GetInstance()
Definition: G4GeometryTolerance.cc:73

Here is the call graph for this function:

Here is the caller graph for this function:

G4Sphere::~G4Sphere ( )

Definition at line 150 of file G4Sphere.cc.

151 {
152 }
G4Sphere::G4Sphere ( __void__ &  a)

Definition at line 133 of file G4Sphere.cc.

134  : G4CSGSolid(a), fRminTolerance(0.), fRmaxTolerance(0.),
135  kAngTolerance(0.), kRadTolerance(0.), fEpsilon(0.),
136  fRmin(0.), fRmax(0.), fSPhi(0.), fDPhi(0.), fSTheta(0.),
137  fDTheta(0.), sinCPhi(0.), cosCPhi(0.), cosHDPhiOT(0.), cosHDPhiIT(0.),
138  sinSPhi(0.), cosSPhi(0.), sinEPhi(0.), cosEPhi(0.), hDPhi(0.), cPhi(0.),
139  ePhi(0.), sinSTheta(0.), cosSTheta(0.), sinETheta(0.), cosETheta(0.),
140  tanSTheta(0.), tanSTheta2(0.), tanETheta(0.), tanETheta2(0.), eTheta(0.),
141  fFullPhiSphere(false), fFullThetaSphere(false), fFullSphere(true),
142  halfCarTolerance(0.), halfAngTolerance(0.)
143 {
144 }
a
std::vector< ExP01TrackerHit * > a
Definition: ExP01Classes.hh:33
G4CSGSolid::G4CSGSolid
G4CSGSolid(const G4String &pName)
Definition: G4CSGSolid.cc:49
G4Sphere::G4Sphere ( const G4Sphere &  rhs)

Definition at line 158 of file G4Sphere.cc.

159  : G4CSGSolid(rhs), fRminTolerance(rhs.fRminTolerance),
160  fRmaxTolerance(rhs.fRmaxTolerance), kAngTolerance(rhs.kAngTolerance),
161  kRadTolerance(rhs.kRadTolerance), fEpsilon(rhs.fEpsilon),
162  fRmin(rhs.fRmin), fRmax(rhs.fRmax), fSPhi(rhs.fSPhi), fDPhi(rhs.fDPhi),
163  fSTheta(rhs.fSTheta), fDTheta(rhs.fDTheta),
164  sinCPhi(rhs.sinCPhi), cosCPhi(rhs.cosCPhi),
165  cosHDPhiOT(rhs.cosHDPhiOT), cosHDPhiIT(rhs.cosHDPhiIT),
166  sinSPhi(rhs.sinSPhi), cosSPhi(rhs.cosSPhi),
167  sinEPhi(rhs.sinEPhi), cosEPhi(rhs.cosEPhi),
168  hDPhi(rhs.hDPhi), cPhi(rhs.cPhi), ePhi(rhs.ePhi),
169  sinSTheta(rhs.sinSTheta), cosSTheta(rhs.cosSTheta),
170  sinETheta(rhs.sinETheta), cosETheta(rhs.cosETheta),
171  tanSTheta(rhs.tanSTheta), tanSTheta2(rhs.tanSTheta2),
172  tanETheta(rhs.tanETheta), tanETheta2(rhs.tanETheta2), eTheta(rhs.eTheta),
173  fFullPhiSphere(rhs.fFullPhiSphere), fFullThetaSphere(rhs.fFullThetaSphere),
174  fFullSphere(rhs.fFullSphere),
175  halfCarTolerance(rhs.halfCarTolerance),
176  halfAngTolerance(rhs.halfAngTolerance)
177 {
178 }
G4CSGSolid::G4CSGSolid
G4CSGSolid(const G4String &pName)
Definition: G4CSGSolid.cc:49

Member Function Documentation

G4bool G4Sphere::CalculateExtent ( const EAxis  pAxis,
const G4VoxelLimits &  pVoxelLimit,
const G4AffineTransform &  pTransform,
G4double &  pmin,
G4double &  pmax 
) const
virtual

Implements G4VSolid.

Definition at line 289 of file G4Sphere.cc.

293 {
294  G4ThreeVector bmin, bmax;
295 
296  // Get bounding box
297  Extent(bmin,bmax);
298 
299  // Find extent
300  G4BoundingEnvelope bbox(bmin,bmax);
301  return bbox.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
302 }
G4Sphere::Extent
void Extent(G4ThreeVector &pMin, G4ThreeVector &pMax) const
Definition: G4Sphere.cc:233

Here is the call graph for this function:

G4VSolid * G4Sphere::Clone ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2764 of file G4Sphere.cc.

2765 {
2766  return new G4Sphere(*this);
2767 }
G4Sphere::G4Sphere
G4Sphere(const G4String &pName, G4double pRmin, G4double pRmax, G4double pSPhi, G4double pDPhi, G4double pSTheta, G4double pDTheta)
Definition: G4Sphere.cc:95

Here is the call graph for this function:

void G4Sphere::ComputeDimensions ( G4VPVParameterisation *  p,
const G4int  n,
const G4VPhysicalVolume *  pRep 
)
virtual

Reimplemented from G4VSolid.

Definition at line 222 of file G4Sphere.cc.

225 {
226  p->ComputeDimensions(*this,n,pRep);
227 }
n
const G4int n
Definition: G4UrQMD1_3Interface.hh:144
G4VPVParameterisation::ComputeDimensions
virtual void ComputeDimensions(G4Box &, const G4int, const G4VPhysicalVolume *) const
Definition: G4VPVParameterisation.hh:95

Here is the call graph for this function:

G4Polyhedron * G4Sphere::CreatePolyhedron ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2937 of file G4Sphere.cc.

2938 {
2939  return new G4PolyhedronSphere (fRmin, fRmax, fSPhi, fDPhi, fSTheta, fDTheta);
2940 }
void G4Sphere::DescribeYourselfTo ( G4VGraphicsScene &  scene) const
virtual

Implements G4VSolid.

Definition at line 2932 of file G4Sphere.cc.

2933 {
2934  scene.AddSolid (*this);
2935 }
G4VGraphicsScene::AddSolid
virtual void AddSolid(const G4Box &)=0

Here is the call graph for this function:

G4double G4Sphere::DistanceToIn ( const G4ThreeVector &  p,
const G4ThreeVector &  v 
) const
virtual

Implements G4VSolid.

Definition at line 726 of file G4Sphere.cc.

728 {
729  G4double snxt = kInfinity ; // snxt = default return value
730  G4double rho2, rad2, pDotV2d, pDotV3d, pTheta ;
731  G4double tolSTheta=0., tolETheta=0. ;
732  const G4double dRmax = 100.*fRmax;
733 
734  const G4double halfRmaxTolerance = fRmaxTolerance*0.5;
735  const G4double halfRminTolerance = fRminTolerance*0.5;
736  const G4double tolORMin2 = (fRmin>halfRminTolerance)
737  ? (fRmin-halfRminTolerance)*(fRmin-halfRminTolerance) : 0;
738  const G4double tolIRMin2 =
739  (fRmin+halfRminTolerance)*(fRmin+halfRminTolerance);
740  const G4double tolORMax2 =
741  (fRmax+halfRmaxTolerance)*(fRmax+halfRmaxTolerance);
742  const G4double tolIRMax2 =
743  (fRmax-halfRmaxTolerance)*(fRmax-halfRmaxTolerance);
744 
745  // Intersection point
746  //
747  G4double xi, yi, zi, rhoi, rhoi2, radi2, iTheta ;
748 
749  // Phi intersection
750  //
751  G4double Comp ;
752 
753  // Phi precalcs
754  //
755  G4double Dist, cosPsi ;
756 
757  // Theta precalcs
758  //
759  G4double dist2STheta, dist2ETheta ;
760  G4double t1, t2, b, c, d2, d, sd = kInfinity ;
761 
762  // General Precalcs
763  //
764  rho2 = p.x()*p.x() + p.y()*p.y() ;
765  rad2 = rho2 + p.z()*p.z() ;
766  pTheta = std::atan2(std::sqrt(rho2),p.z()) ;
767 
768  pDotV2d = p.x()*v.x() + p.y()*v.y() ;
769  pDotV3d = pDotV2d + p.z()*v.z() ;
770 
771  // Theta precalcs
772  //
773  if (!fFullThetaSphere)
774  {
775  tolSTheta = fSTheta - halfAngTolerance ;
776  tolETheta = eTheta + halfAngTolerance ;
777 
778  // Special case rad2 = 0 comparing with direction
779  //
780  if ((rad2!=0.0) || (fRmin!=0.0))
781  {
782  // Keep going for computation of distance...
783  }
784  else // Positioned on the sphere's origin
785  {
786  G4double vTheta = std::atan2(std::sqrt(v.x()*v.x()+v.y()*v.y()),v.z()) ;
787  if ( (vTheta < tolSTheta) || (vTheta > tolETheta) )
788  {
789  return snxt ; // kInfinity
790  }
791  return snxt = 0.0 ;
792  }
793  }
794 
795  // Outer spherical shell intersection
796  // - Only if outside tolerant fRmax
797  // - Check for if inside and outer G4Sphere heading through solid (-> 0)
798  // - No intersect -> no intersection with G4Sphere
799  //
800  // Shell eqn: x^2+y^2+z^2=RSPH^2
801  //
802  // => (px+svx)^2+(py+svy)^2+(pz+svz)^2=R^2
803  //
804  // => (px^2+py^2+pz^2) +2sd(pxvx+pyvy+pzvz)+sd^2(vx^2+vy^2+vz^2)=R^2
805  // => rad2 +2sd(pDotV3d) +sd^2 =R^2
806  //
807  // => sd=-pDotV3d+-std::sqrt(pDotV3d^2-(rad2-R^2))
808 
809  c = rad2 - fRmax*fRmax ;
810 
811  if (c > fRmaxTolerance*fRmax)
812  {
813  // If outside tolerant boundary of outer G4Sphere
814  // [should be std::sqrt(rad2)-fRmax > halfRmaxTolerance]
815 
816  d2 = pDotV3d*pDotV3d - c ;
817 
818  if ( d2 >= 0 )
819  {
820  sd = -pDotV3d - std::sqrt(d2) ;
821 
822  if (sd >= 0 )
823  {
824  if ( sd>dRmax ) // Avoid rounding errors due to precision issues seen on
825  { // 64 bits systems. Split long distances and recompute
826  G4double fTerm = sd-std::fmod(sd,dRmax);
827  sd = fTerm + DistanceToIn(p+fTerm*v,v);
828  }
829  xi = p.x() + sd*v.x() ;
830  yi = p.y() + sd*v.y() ;
831  rhoi = std::sqrt(xi*xi + yi*yi) ;
832 
833  if (!fFullPhiSphere && rhoi) // Check phi intersection
834  {
835  cosPsi = (xi*cosCPhi + yi*sinCPhi)/rhoi ;
836 
837  if (cosPsi >= cosHDPhiOT)
838  {
839  if (!fFullThetaSphere) // Check theta intersection
840  {
841  zi = p.z() + sd*v.z() ;
842 
843  // rhoi & zi can never both be 0
844  // (=>intersect at origin =>fRmax=0)
845  //
846  iTheta = std::atan2(rhoi,zi) ;
847  if ( (iTheta >= tolSTheta) && (iTheta <= tolETheta) )
848  {
849  return snxt = sd ;
850  }
851  }
852  else
853  {
854  return snxt=sd;
855  }
856  }
857  }
858  else
859  {
860  if (!fFullThetaSphere) // Check theta intersection
861  {
862  zi = p.z() + sd*v.z() ;
863 
864  // rhoi & zi can never both be 0
865  // (=>intersect at origin => fRmax=0 !)
866  //
867  iTheta = std::atan2(rhoi,zi) ;
868  if ( (iTheta >= tolSTheta) && (iTheta <= tolETheta) )
869  {
870  return snxt=sd;
871  }
872  }
873  else
874  {
875  return snxt = sd;
876  }
877  }
878  }
879  }
880  else // No intersection with G4Sphere
881  {
882  return snxt=kInfinity;
883  }
884  }
885  else
886  {
887  // Inside outer radius
888  // check not inside, and heading through G4Sphere (-> 0 to in)
889 
890  d2 = pDotV3d*pDotV3d - c ;
891 
892  if ( (rad2 > tolIRMax2)
893  && ( (d2 >= fRmaxTolerance*fRmax) && (pDotV3d < 0) ) )
894  {
895  if (!fFullPhiSphere)
896  {
897  // Use inner phi tolerant boundary -> if on tolerant
898  // phi boundaries, phi intersect code handles leaving/entering checks
899 
900  cosPsi = (p.x()*cosCPhi + p.y()*sinCPhi)/std::sqrt(rho2) ;
901 
902  if (cosPsi>=cosHDPhiIT)
903  {
904  // inside radii, delta r -ve, inside phi
905 
906  if ( !fFullThetaSphere )
907  {
908  if ( (pTheta >= tolSTheta + kAngTolerance)
909  && (pTheta <= tolETheta - kAngTolerance) )
910  {
911  return snxt=0;
912  }
913  }
914  else // strictly inside Theta in both cases
915  {
916  return snxt=0;
917  }
918  }
919  }
920  else
921  {
922  if ( !fFullThetaSphere )
923  {
924  if ( (pTheta >= tolSTheta + kAngTolerance)
925  && (pTheta <= tolETheta - kAngTolerance) )
926  {
927  return snxt=0;
928  }
929  }
930  else // strictly inside Theta in both cases
931  {
932  return snxt=0;
933  }
934  }
935  }
936  }
937 
938  // Inner spherical shell intersection
939  // - Always farthest root, because would have passed through outer
940  // surface first.
941  // - Tolerant check if travelling through solid
942 
943  if (fRmin)
944  {
945  c = rad2 - fRmin*fRmin ;
946  d2 = pDotV3d*pDotV3d - c ;
947 
948  // Within tolerance inner radius of inner G4Sphere
949  // Check for immediate entry/already inside and travelling outwards
950 
951  if ( (c > -halfRminTolerance) && (rad2 < tolIRMin2)
952  && ( (d2 < fRmin*kCarTolerance) || (pDotV3d >= 0) ) )
953  {
954  if ( !fFullPhiSphere )
955  {
956  // Use inner phi tolerant boundary -> if on tolerant
957  // phi boundaries, phi intersect code handles leaving/entering checks
958 
959  cosPsi = (p.x()*cosCPhi+p.y()*sinCPhi)/std::sqrt(rho2) ;
960  if (cosPsi >= cosHDPhiIT)
961  {
962  // inside radii, delta r -ve, inside phi
963  //
964  if ( !fFullThetaSphere )
965  {
966  if ( (pTheta >= tolSTheta + kAngTolerance)
967  && (pTheta <= tolETheta - kAngTolerance) )
968  {
969  return snxt=0;
970  }
971  }
972  else
973  {
974  return snxt = 0 ;
975  }
976  }
977  }
978  else
979  {
980  if ( !fFullThetaSphere )
981  {
982  if ( (pTheta >= tolSTheta + kAngTolerance)
983  && (pTheta <= tolETheta - kAngTolerance) )
984  {
985  return snxt = 0 ;
986  }
987  }
988  else
989  {
990  return snxt=0;
991  }
992  }
993  }
994  else // Not special tolerant case
995  {
996  if (d2 >= 0)
997  {
998  sd = -pDotV3d + std::sqrt(d2) ;
999  if ( sd >= halfRminTolerance ) // It was >= 0 ??
1000  {
1001  xi = p.x() + sd*v.x() ;
1002  yi = p.y() + sd*v.y() ;
1003  rhoi = std::sqrt(xi*xi+yi*yi) ;
1004 
1005  if ( !fFullPhiSphere && rhoi ) // Check phi intersection
1006  {
1007  cosPsi = (xi*cosCPhi + yi*sinCPhi)/rhoi ;
1008 
1009  if (cosPsi >= cosHDPhiOT)
1010  {
1011  if ( !fFullThetaSphere ) // Check theta intersection
1012  {
1013  zi = p.z() + sd*v.z() ;
1014 
1015  // rhoi & zi can never both be 0
1016  // (=>intersect at origin =>fRmax=0)
1017  //
1018  iTheta = std::atan2(rhoi,zi) ;
1019  if ( (iTheta >= tolSTheta) && (iTheta<=tolETheta) )
1020  {
1021  snxt = sd;
1022  }
1023  }
1024  else
1025  {
1026  snxt=sd;
1027  }
1028  }
1029  }
1030  else
1031  {
1032  if ( !fFullThetaSphere ) // Check theta intersection
1033  {
1034  zi = p.z() + sd*v.z() ;
1035 
1036  // rhoi & zi can never both be 0
1037  // (=>intersect at origin => fRmax=0 !)
1038  //
1039  iTheta = std::atan2(rhoi,zi) ;
1040  if ( (iTheta >= tolSTheta) && (iTheta <= tolETheta) )
1041  {
1042  snxt = sd;
1043  }
1044  }
1045  else
1046  {
1047  snxt = sd;
1048  }
1049  }
1050  }
1051  }
1052  }
1053  }
1054 
1055  // Phi segment intersection
1056  //
1057  // o Tolerant of points inside phi planes by up to kCarTolerance*0.5
1058  //
1059  // o NOTE: Large duplication of code between sphi & ephi checks
1060  // -> only diffs: sphi -> ephi, Comp -> -Comp and half-plane
1061  // intersection check <=0 -> >=0
1062  // -> Should use some form of loop Construct
1063  //
1064  if ( !fFullPhiSphere )
1065  {
1066  // First phi surface ('S'tarting phi)
1067  // Comp = Component in outwards normal dirn
1068  //
1069  Comp = v.x()*sinSPhi - v.y()*cosSPhi ;
1070 
1071  if ( Comp < 0 )
1072  {
1073  Dist = p.y()*cosSPhi - p.x()*sinSPhi ;
1074 
1075  if (Dist < halfCarTolerance)
1076  {
1077  sd = Dist/Comp ;
1078 
1079  if (sd < snxt)
1080  {
1081  if ( sd > 0 )
1082  {
1083  xi = p.x() + sd*v.x() ;
1084  yi = p.y() + sd*v.y() ;
1085  zi = p.z() + sd*v.z() ;
1086  rhoi2 = xi*xi + yi*yi ;
1087  radi2 = rhoi2 + zi*zi ;
1088  }
1089  else
1090  {
1091  sd = 0 ;
1092  xi = p.x() ;
1093  yi = p.y() ;
1094  zi = p.z() ;
1095  rhoi2 = rho2 ;
1096  radi2 = rad2 ;
1097  }
1098  if ( (radi2 <= tolORMax2)
1099  && (radi2 >= tolORMin2)
1100  && ((yi*cosCPhi-xi*sinCPhi) <= 0) )
1101  {
1102  // Check theta intersection
1103  // rhoi & zi can never both be 0
1104  // (=>intersect at origin =>fRmax=0)
1105  //
1106  if ( !fFullThetaSphere )
1107  {
1108  iTheta = std::atan2(std::sqrt(rhoi2),zi) ;
1109  if ( (iTheta >= tolSTheta) && (iTheta <= tolETheta) )
1110  {
1111  // r and theta intersections good
1112  // - check intersecting with correct half-plane
1113 
1114  if ((yi*cosCPhi-xi*sinCPhi) <= 0)
1115  {
1116  snxt = sd;
1117  }
1118  }
1119  }
1120  else
1121  {
1122  snxt = sd;
1123  }
1124  }
1125  }
1126  }
1127  }
1128 
1129  // Second phi surface ('E'nding phi)
1130  // Component in outwards normal dirn
1131 
1132  Comp = -( v.x()*sinEPhi-v.y()*cosEPhi ) ;
1133 
1134  if (Comp < 0)
1135  {
1136  Dist = -(p.y()*cosEPhi-p.x()*sinEPhi) ;
1137  if ( Dist < halfCarTolerance )
1138  {
1139  sd = Dist/Comp ;
1140 
1141  if ( sd < snxt )
1142  {
1143  if (sd > 0)
1144  {
1145  xi = p.x() + sd*v.x() ;
1146  yi = p.y() + sd*v.y() ;
1147  zi = p.z() + sd*v.z() ;
1148  rhoi2 = xi*xi + yi*yi ;
1149  radi2 = rhoi2 + zi*zi ;
1150  }
1151  else
1152  {
1153  sd = 0 ;
1154  xi = p.x() ;
1155  yi = p.y() ;
1156  zi = p.z() ;
1157  rhoi2 = rho2 ;
1158  radi2 = rad2 ;
1159  }
1160  if ( (radi2 <= tolORMax2)
1161  && (radi2 >= tolORMin2)
1162  && ((yi*cosCPhi-xi*sinCPhi) >= 0) )
1163  {
1164  // Check theta intersection
1165  // rhoi & zi can never both be 0
1166  // (=>intersect at origin =>fRmax=0)
1167  //
1168  if ( !fFullThetaSphere )
1169  {
1170  iTheta = std::atan2(std::sqrt(rhoi2),zi) ;
1171  if ( (iTheta >= tolSTheta) && (iTheta <= tolETheta) )
1172  {
1173  // r and theta intersections good
1174  // - check intersecting with correct half-plane
1175 
1176  if ((yi*cosCPhi-xi*sinCPhi) >= 0)
1177  {
1178  snxt = sd;
1179  }
1180  }
1181  }
1182  else
1183  {
1184  snxt = sd;
1185  }
1186  }
1187  }
1188  }
1189  }
1190  }
1191 
1192  // Theta segment intersection
1193 
1194  if ( !fFullThetaSphere )
1195  {
1196 
1197  // Intersection with theta surfaces
1198  // Known failure cases:
1199  // o Inside tolerance of stheta surface, skim
1200  // ~parallel to cone and Hit & enter etheta surface [& visa versa]
1201  //
1202  // To solve: Check 2nd root of etheta surface in addition to stheta
1203  //
1204  // o start/end theta is exactly pi/2
1205  // Intersections with cones
1206  //
1207  // Cone equation: x^2+y^2=z^2tan^2(t)
1208  //
1209  // => (px+svx)^2+(py+svy)^2=(pz+svz)^2tan^2(t)
1210  //
1211  // => (px^2+py^2-pz^2tan^2(t))+2sd(pxvx+pyvy-pzvztan^2(t))
1212  // + sd^2(vx^2+vy^2-vz^2tan^2(t)) = 0
1213  //
1214  // => sd^2(1-vz^2(1+tan^2(t))+2sd(pdotv2d-pzvztan^2(t))
1215  // + (rho2-pz^2tan^2(t)) = 0
1216 
1217  if (fSTheta)
1218  {
1219  dist2STheta = rho2 - p.z()*p.z()*tanSTheta2 ;
1220  }
1221  else
1222  {
1223  dist2STheta = kInfinity ;
1224  }
1225  if ( eTheta < pi )
1226  {
1227  dist2ETheta=rho2-p.z()*p.z()*tanETheta2;
1228  }
1229  else
1230  {
1231  dist2ETheta=kInfinity;
1232  }
1233  if ( pTheta < tolSTheta )
1234  {
1235  // Inside (theta<stheta-tol) stheta cone
1236  // First root of stheta cone, second if first root -ve
1237 
1238  t1 = 1 - v.z()*v.z()*(1 + tanSTheta2) ;
1239  t2 = pDotV2d - p.z()*v.z()*tanSTheta2 ;
1240  if (t1)
1241  {
1242  b = t2/t1 ;
1243  c = dist2STheta/t1 ;
1244  d2 = b*b - c ;
1245 
1246  if ( d2 >= 0 )
1247  {
1248  d = std::sqrt(d2) ;
1249  sd = -b - d ; // First root
1250  zi = p.z() + sd*v.z();
1251 
1252  if ( (sd < 0) || (zi*(fSTheta - halfpi) > 0) )
1253  {
1254  sd = -b+d; // Second root
1255  }
1256  if ((sd >= 0) && (sd < snxt))
1257  {
1258  xi = p.x() + sd*v.x();
1259  yi = p.y() + sd*v.y();
1260  zi = p.z() + sd*v.z();
1261  rhoi2 = xi*xi + yi*yi;
1262  radi2 = rhoi2 + zi*zi;
1263  if ( (radi2 <= tolORMax2)
1264  && (radi2 >= tolORMin2)
1265  && (zi*(fSTheta - halfpi) <= 0) )
1266  {
1267  if ( !fFullPhiSphere && rhoi2 ) // Check phi intersection
1268  {
1269  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1270  if (cosPsi >= cosHDPhiOT)
1271  {
1272  snxt = sd;
1273  }
1274  }
1275  else
1276  {
1277  snxt = sd;
1278  }
1279  }
1280  }
1281  }
1282  }
1283 
1284  // Possible intersection with ETheta cone.
1285  // Second >= 0 root should be considered
1286 
1287  if ( eTheta < pi )
1288  {
1289  t1 = 1 - v.z()*v.z()*(1 + tanETheta2) ;
1290  t2 = pDotV2d - p.z()*v.z()*tanETheta2 ;
1291  if (t1)
1292  {
1293  b = t2/t1 ;
1294  c = dist2ETheta/t1 ;
1295  d2 = b*b - c ;
1296 
1297  if (d2 >= 0)
1298  {
1299  d = std::sqrt(d2) ;
1300  sd = -b + d ; // Second root
1301 
1302  if ( (sd >= 0) && (sd < snxt) )
1303  {
1304  xi = p.x() + sd*v.x() ;
1305  yi = p.y() + sd*v.y() ;
1306  zi = p.z() + sd*v.z() ;
1307  rhoi2 = xi*xi + yi*yi ;
1308  radi2 = rhoi2 + zi*zi ;
1309 
1310  if ( (radi2 <= tolORMax2)
1311  && (radi2 >= tolORMin2)
1312  && (zi*(eTheta - halfpi) <= 0) )
1313  {
1314  if (!fFullPhiSphere && rhoi2) // Check phi intersection
1315  {
1316  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1317  if (cosPsi >= cosHDPhiOT)
1318  {
1319  snxt = sd;
1320  }
1321  }
1322  else
1323  {
1324  snxt = sd;
1325  }
1326  }
1327  }
1328  }
1329  }
1330  }
1331  }
1332  else if ( pTheta > tolETheta )
1333  {
1334  // dist2ETheta<-kRadTolerance*0.5 && dist2STheta>0)
1335  // Inside (theta > etheta+tol) e-theta cone
1336  // First root of etheta cone, second if first root 'imaginary'
1337 
1338  t1 = 1 - v.z()*v.z()*(1 + tanETheta2) ;
1339  t2 = pDotV2d - p.z()*v.z()*tanETheta2 ;
1340  if (t1)
1341  {
1342  b = t2/t1 ;
1343  c = dist2ETheta/t1 ;
1344  d2 = b*b - c ;
1345 
1346  if (d2 >= 0)
1347  {
1348  d = std::sqrt(d2) ;
1349  sd = -b - d ; // First root
1350  zi = p.z() + sd*v.z();
1351 
1352  if ( (sd < 0) || (zi*(eTheta - halfpi) > 0) )
1353  {
1354  sd = -b + d ; // second root
1355  }
1356  if ( (sd >= 0) && (sd < snxt) )
1357  {
1358  xi = p.x() + sd*v.x() ;
1359  yi = p.y() + sd*v.y() ;
1360  zi = p.z() + sd*v.z() ;
1361  rhoi2 = xi*xi + yi*yi ;
1362  radi2 = rhoi2 + zi*zi ;
1363 
1364  if ( (radi2 <= tolORMax2)
1365  && (radi2 >= tolORMin2)
1366  && (zi*(eTheta - halfpi) <= 0) )
1367  {
1368  if (!fFullPhiSphere && rhoi2) // Check phi intersection
1369  {
1370  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1371  if (cosPsi >= cosHDPhiOT)
1372  {
1373  snxt = sd;
1374  }
1375  }
1376  else
1377  {
1378  snxt = sd;
1379  }
1380  }
1381  }
1382  }
1383  }
1384 
1385  // Possible intersection with STheta cone.
1386  // Second >= 0 root should be considered
1387 
1388  if ( fSTheta )
1389  {
1390  t1 = 1 - v.z()*v.z()*(1 + tanSTheta2) ;
1391  t2 = pDotV2d - p.z()*v.z()*tanSTheta2 ;
1392  if (t1)
1393  {
1394  b = t2/t1 ;
1395  c = dist2STheta/t1 ;
1396  d2 = b*b - c ;
1397 
1398  if (d2 >= 0)
1399  {
1400  d = std::sqrt(d2) ;
1401  sd = -b + d ; // Second root
1402 
1403  if ( (sd >= 0) && (sd < snxt) )
1404  {
1405  xi = p.x() + sd*v.x() ;
1406  yi = p.y() + sd*v.y() ;
1407  zi = p.z() + sd*v.z() ;
1408  rhoi2 = xi*xi + yi*yi ;
1409  radi2 = rhoi2 + zi*zi ;
1410 
1411  if ( (radi2 <= tolORMax2)
1412  && (radi2 >= tolORMin2)
1413  && (zi*(fSTheta - halfpi) <= 0) )
1414  {
1415  if (!fFullPhiSphere && rhoi2) // Check phi intersection
1416  {
1417  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1418  if (cosPsi >= cosHDPhiOT)
1419  {
1420  snxt = sd;
1421  }
1422  }
1423  else
1424  {
1425  snxt = sd;
1426  }
1427  }
1428  }
1429  }
1430  }
1431  }
1432  }
1433  else if ( (pTheta < tolSTheta + kAngTolerance)
1434  && (fSTheta > halfAngTolerance) )
1435  {
1436  // In tolerance of stheta
1437  // If entering through solid [r,phi] => 0 to in
1438  // else try 2nd root
1439 
1440  t2 = pDotV2d - p.z()*v.z()*tanSTheta2 ;
1441  if ( (t2>=0 && tolIRMin2<rad2 && rad2<tolIRMax2 && fSTheta<halfpi)
1442  || (t2<0 && tolIRMin2<rad2 && rad2<tolIRMax2 && fSTheta>halfpi)
1443  || (v.z()<0 && tolIRMin2<rad2 && rad2<tolIRMax2 && fSTheta==halfpi) )
1444  {
1445  if (!fFullPhiSphere && rho2) // Check phi intersection
1446  {
1447  cosPsi = (p.x()*cosCPhi + p.y()*sinCPhi)/std::sqrt(rho2) ;
1448  if (cosPsi >= cosHDPhiIT)
1449  {
1450  return 0 ;
1451  }
1452  }
1453  else
1454  {
1455  return 0 ;
1456  }
1457  }
1458 
1459  // Not entering immediately/travelling through
1460 
1461  t1 = 1 - v.z()*v.z()*(1 + tanSTheta2) ;
1462  if (t1)
1463  {
1464  b = t2/t1 ;
1465  c = dist2STheta/t1 ;
1466  d2 = b*b - c ;
1467 
1468  if (d2 >= 0)
1469  {
1470  d = std::sqrt(d2) ;
1471  sd = -b + d ;
1472  if ( (sd >= halfCarTolerance) && (sd < snxt) && (fSTheta < halfpi) )
1473  { // ^^^^^^^^^^^^^^^^^^^^^ shouldn't it be >=0 instead ?
1474  xi = p.x() + sd*v.x() ;
1475  yi = p.y() + sd*v.y() ;
1476  zi = p.z() + sd*v.z() ;
1477  rhoi2 = xi*xi + yi*yi ;
1478  radi2 = rhoi2 + zi*zi ;
1479 
1480  if ( (radi2 <= tolORMax2)
1481  && (radi2 >= tolORMin2)
1482  && (zi*(fSTheta - halfpi) <= 0) )
1483  {
1484  if ( !fFullPhiSphere && rhoi2 ) // Check phi intersection
1485  {
1486  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1487  if ( cosPsi >= cosHDPhiOT )
1488  {
1489  snxt = sd;
1490  }
1491  }
1492  else
1493  {
1494  snxt = sd;
1495  }
1496  }
1497  }
1498  }
1499  }
1500  }
1501  else if ((pTheta > tolETheta-kAngTolerance) && (eTheta < pi-kAngTolerance))
1502  {
1503 
1504  // In tolerance of etheta
1505  // If entering through solid [r,phi] => 0 to in
1506  // else try 2nd root
1507 
1508  t2 = pDotV2d - p.z()*v.z()*tanETheta2 ;
1509 
1510  if ( ((t2<0) && (eTheta < halfpi)
1511  && (tolIRMin2 < rad2) && (rad2 < tolIRMax2))
1512  || ((t2>=0) && (eTheta > halfpi)
1513  && (tolIRMin2 < rad2) && (rad2 < tolIRMax2))
1514  || ((v.z()>0) && (eTheta == halfpi)
1515  && (tolIRMin2 < rad2) && (rad2 < tolIRMax2)) )
1516  {
1517  if (!fFullPhiSphere && rho2) // Check phi intersection
1518  {
1519  cosPsi = (p.x()*cosCPhi + p.y()*sinCPhi)/std::sqrt(rho2) ;
1520  if (cosPsi >= cosHDPhiIT)
1521  {
1522  return 0 ;
1523  }
1524  }
1525  else
1526  {
1527  return 0 ;
1528  }
1529  }
1530 
1531  // Not entering immediately/travelling through
1532 
1533  t1 = 1 - v.z()*v.z()*(1 + tanETheta2) ;
1534  if (t1)
1535  {
1536  b = t2/t1 ;
1537  c = dist2ETheta/t1 ;
1538  d2 = b*b - c ;
1539 
1540  if (d2 >= 0)
1541  {
1542  d = std::sqrt(d2) ;
1543  sd = -b + d ;
1544 
1545  if ( (sd >= halfCarTolerance)
1546  && (sd < snxt) && (eTheta > halfpi) )
1547  {
1548  xi = p.x() + sd*v.x() ;
1549  yi = p.y() + sd*v.y() ;
1550  zi = p.z() + sd*v.z() ;
1551  rhoi2 = xi*xi + yi*yi ;
1552  radi2 = rhoi2 + zi*zi ;
1553 
1554  if ( (radi2 <= tolORMax2)
1555  && (radi2 >= tolORMin2)
1556  && (zi*(eTheta - halfpi) <= 0) )
1557  {
1558  if (!fFullPhiSphere && rhoi2) // Check phi intersection
1559  {
1560  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1561  if (cosPsi >= cosHDPhiOT)
1562  {
1563  snxt = sd;
1564  }
1565  }
1566  else
1567  {
1568  snxt = sd;
1569  }
1570  }
1571  }
1572  }
1573  }
1574  }
1575  else
1576  {
1577  // stheta+tol<theta<etheta-tol
1578  // For BOTH stheta & etheta check 2nd root for validity [r,phi]
1579 
1580  t1 = 1 - v.z()*v.z()*(1 + tanSTheta2) ;
1581  t2 = pDotV2d - p.z()*v.z()*tanSTheta2 ;
1582  if (t1)
1583  {
1584  b = t2/t1;
1585  c = dist2STheta/t1 ;
1586  d2 = b*b - c ;
1587 
1588  if (d2 >= 0)
1589  {
1590  d = std::sqrt(d2) ;
1591  sd = -b + d ; // second root
1592 
1593  if ((sd >= 0) && (sd < snxt))
1594  {
1595  xi = p.x() + sd*v.x() ;
1596  yi = p.y() + sd*v.y() ;
1597  zi = p.z() + sd*v.z() ;
1598  rhoi2 = xi*xi + yi*yi ;
1599  radi2 = rhoi2 + zi*zi ;
1600 
1601  if ( (radi2 <= tolORMax2)
1602  && (radi2 >= tolORMin2)
1603  && (zi*(fSTheta - halfpi) <= 0) )
1604  {
1605  if (!fFullPhiSphere && rhoi2) // Check phi intersection
1606  {
1607  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1608  if (cosPsi >= cosHDPhiOT)
1609  {
1610  snxt = sd;
1611  }
1612  }
1613  else
1614  {
1615  snxt = sd;
1616  }
1617  }
1618  }
1619  }
1620  }
1621  t1 = 1 - v.z()*v.z()*(1 + tanETheta2) ;
1622  t2 = pDotV2d - p.z()*v.z()*tanETheta2 ;
1623  if (t1)
1624  {
1625  b = t2/t1 ;
1626  c = dist2ETheta/t1 ;
1627  d2 = b*b - c ;
1628 
1629  if (d2 >= 0)
1630  {
1631  d = std::sqrt(d2) ;
1632  sd = -b + d; // second root
1633 
1634  if ((sd >= 0) && (sd < snxt))
1635  {
1636  xi = p.x() + sd*v.x() ;
1637  yi = p.y() + sd*v.y() ;
1638  zi = p.z() + sd*v.z() ;
1639  rhoi2 = xi*xi + yi*yi ;
1640  radi2 = rhoi2 + zi*zi ;
1641 
1642  if ( (radi2 <= tolORMax2)
1643  && (radi2 >= tolORMin2)
1644  && (zi*(eTheta - halfpi) <= 0) )
1645  {
1646  if (!fFullPhiSphere && rhoi2) // Check phi intersection
1647  {
1648  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
1649  if ( cosPsi >= cosHDPhiOT )
1650  {
1651  snxt = sd;
1652  }
1653  }
1654  else
1655  {
1656  snxt = sd;
1657  }
1658  }
1659  }
1660  }
1661  }
1662  }
1663  }
1664  return snxt;
1665 }
G4Sphere::DistanceToIn
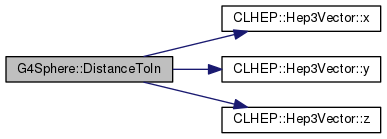
G4double DistanceToIn(const G4ThreeVector &p, const G4ThreeVector &v) const
Definition: G4Sphere.cc:726
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
CLHEP::Hep3Vector::x
double x() const
d2
static const G4double d2
Definition: G4ElectroNuclearCrossSection.cc:89
CLHEP::Hep3Vector::z
double z() const
test.b
tuple b
Definition: test.py:12
plottest35.t1
tuple t1
Definition: plottest35.py:33
CLHEP::Hep3Vector::y
double y() const
G4VSolid::kCarTolerance
G4double kCarTolerance
Definition: G4VSolid.hh:307
pi
static constexpr double pi
Definition: G4SIunits.hh:75
halfpi
static constexpr double halfpi
Definition: G4SIunits.hh:77
G4double
double G4double
Definition: G4Types.hh:76
test.c
tuple c
Definition: test.py:13

Here is the call graph for this function:

G4double G4Sphere::DistanceToIn ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 1675 of file G4Sphere.cc.

1676 {
1677  G4double safe=0.0,safeRMin,safeRMax,safePhi,safeTheta;
1678  G4double rho2,rds,rho;
1679  G4double cosPsi;
1680  G4double pTheta,dTheta1,dTheta2;
1681  rho2=p.x()*p.x()+p.y()*p.y();
1682  rds=std::sqrt(rho2+p.z()*p.z());
1683  rho=std::sqrt(rho2);
1684 
1685  //
1686  // Distance to r shells
1687  //
1688  if (fRmin)
1689  {
1690  safeRMin=fRmin-rds;
1691  safeRMax=rds-fRmax;
1692  if (safeRMin>safeRMax)
1693  {
1694  safe=safeRMin;
1695  }
1696  else
1697  {
1698  safe=safeRMax;
1699  }
1700  }
1701  else
1702  {
1703  safe=rds-fRmax;
1704  }
1705 
1706  //
1707  // Distance to phi extent
1708  //
1709  if (!fFullPhiSphere && rho)
1710  {
1711  // Psi=angle from central phi to point
1712  //
1713  cosPsi=(p.x()*cosCPhi+p.y()*sinCPhi)/rho;
1714  if (cosPsi<std::cos(hDPhi))
1715  {
1716  // Point lies outside phi range
1717  //
1718  if ((p.y()*cosCPhi-p.x()*sinCPhi)<=0)
1719  {
1720  safePhi=std::fabs(p.x()*sinSPhi-p.y()*cosSPhi);
1721  }
1722  else
1723  {
1724  safePhi=std::fabs(p.x()*sinEPhi-p.y()*cosEPhi);
1725  }
1726  if (safePhi>safe) { safe=safePhi; }
1727  }
1728  }
1729  //
1730  // Distance to Theta extent
1731  //
1732  if ((rds!=0.0) && (!fFullThetaSphere))
1733  {
1734  pTheta=std::acos(p.z()/rds);
1735  if (pTheta<0) { pTheta+=pi; }
1736  dTheta1=fSTheta-pTheta;
1737  dTheta2=pTheta-eTheta;
1738  if (dTheta1>dTheta2)
1739  {
1740  if (dTheta1>=0) // WHY ???????????
1741  {
1742  safeTheta=rds*std::sin(dTheta1);
1743  if (safe<=safeTheta)
1744  {
1745  safe=safeTheta;
1746  }
1747  }
1748  }
1749  else
1750  {
1751  if (dTheta2>=0)
1752  {
1753  safeTheta=rds*std::sin(dTheta2);
1754  if (safe<=safeTheta)
1755  {
1756  safe=safeTheta;
1757  }
1758  }
1759  }
1760  }
1761 
1762  if (safe<0) { safe=0; }
1763  return safe;
1764 }
CLHEP::Hep3Vector::x
double x() const
CLHEP::Hep3Vector::z
double z() const
CLHEP::Hep3Vector::y
double y() const
pi
static constexpr double pi
Definition: G4SIunits.hh:75
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

G4double G4Sphere::DistanceToOut ( const G4ThreeVector &  p,
const G4ThreeVector &  v,
const G4bool  calcNorm = G4bool(false),
G4bool *  validNorm = 0,
G4ThreeVector *  n = 0 
) const
virtual

Implements G4VSolid.

Definition at line 1771 of file G4Sphere.cc.

1776 {
1777  G4double snxt = kInfinity; // snxt is default return value
1778  G4double sphi= kInfinity,stheta= kInfinity;
1779  ESide side=kNull,sidephi=kNull,sidetheta=kNull;
1780 
1781  const G4double halfRmaxTolerance = fRmaxTolerance*0.5;
1782  const G4double halfRminTolerance = fRminTolerance*0.5;
1783  const G4double Rmax_plus = fRmax + halfRmaxTolerance;
1784  const G4double Rmin_minus = (fRmin) ? fRmin-halfRminTolerance : 0;
1785  G4double t1,t2;
1786  G4double b,c,d;
1787 
1788  // Variables for phi intersection:
1789 
1790  G4double pDistS,compS,pDistE,compE,sphi2,vphi;
1791 
1792  G4double rho2,rad2,pDotV2d,pDotV3d;
1793 
1794  G4double xi,yi,zi; // Intersection point
1795 
1796  // Theta precals
1797  //
1798  G4double rhoSecTheta;
1799  G4double dist2STheta, dist2ETheta, distTheta;
1800  G4double d2,sd;
1801 
1802  // General Precalcs
1803  //
1804  rho2 = p.x()*p.x()+p.y()*p.y();
1805  rad2 = rho2+p.z()*p.z();
1806 
1807  pDotV2d = p.x()*v.x()+p.y()*v.y();
1808  pDotV3d = pDotV2d+p.z()*v.z();
1809 
1810  // Radial Intersections from G4Sphere::DistanceToIn
1811  //
1812  // Outer spherical shell intersection
1813  // - Only if outside tolerant fRmax
1814  // - Check for if inside and outer G4Sphere heading through solid (-> 0)
1815  // - No intersect -> no intersection with G4Sphere
1816  //
1817  // Shell eqn: x^2+y^2+z^2=RSPH^2
1818  //
1819  // => (px+svx)^2+(py+svy)^2+(pz+svz)^2=R^2
1820  //
1821  // => (px^2+py^2+pz^2) +2sd(pxvx+pyvy+pzvz)+sd^2(vx^2+vy^2+vz^2)=R^2
1822  // => rad2 +2sd(pDotV3d) +sd^2 =R^2
1823  //
1824  // => sd=-pDotV3d+-std::sqrt(pDotV3d^2-(rad2-R^2))
1825 
1826  if( (rad2 <= Rmax_plus*Rmax_plus) && (rad2 >= Rmin_minus*Rmin_minus) )
1827  {
1828  c = rad2 - fRmax*fRmax;
1829 
1830  if (c < fRmaxTolerance*fRmax)
1831  {
1832  // Within tolerant Outer radius
1833  //
1834  // The test is
1835  // rad - fRmax < 0.5*kRadTolerance
1836  // => rad < fRmax + 0.5*kRadTol
1837  // => rad2 < (fRmax + 0.5*kRadTol)^2
1838  // => rad2 < fRmax^2 + 2.*0.5*fRmax*kRadTol + 0.25*kRadTol*kRadTol
1839  // => rad2 - fRmax^2 <~ fRmax*kRadTol
1840 
1841  d2 = pDotV3d*pDotV3d - c;
1842 
1843  if( (c >- fRmaxTolerance*fRmax) // on tolerant surface
1844  && ((pDotV3d >=0) || (d2 < 0)) ) // leaving outside from Rmax
1845  // not re-entering
1846  {
1847  if(calcNorm)
1848  {
1849  *validNorm = true ;
1850  *n = G4ThreeVector(p.x()/fRmax,p.y()/fRmax,p.z()/fRmax) ;
1851  }
1852  return snxt = 0;
1853  }
1854  else
1855  {
1856  snxt = -pDotV3d+std::sqrt(d2); // second root since inside Rmax
1857  side = kRMax ;
1858  }
1859  }
1860 
1861  // Inner spherical shell intersection:
1862  // Always first >=0 root, because would have passed
1863  // from outside of Rmin surface .
1864 
1865  if (fRmin)
1866  {
1867  c = rad2 - fRmin*fRmin;
1868  d2 = pDotV3d*pDotV3d - c;
1869 
1870  if (c >- fRminTolerance*fRmin) // 2.0 * (0.5*kRadTolerance) * fRmin
1871  {
1872  if ( (c < fRminTolerance*fRmin) // leaving from Rmin
1873  && (d2 >= fRminTolerance*fRmin) && (pDotV3d < 0) )
1874  {
1875  if(calcNorm) { *validNorm = false; } // Rmin surface is concave
1876  return snxt = 0 ;
1877  }
1878  else
1879  {
1880  if ( d2 >= 0. )
1881  {
1882  sd = -pDotV3d-std::sqrt(d2);
1883 
1884  if ( sd >= 0. ) // Always intersect Rmin first
1885  {
1886  snxt = sd ;
1887  side = kRMin ;
1888  }
1889  }
1890  }
1891  }
1892  }
1893  }
1894 
1895  // Theta segment intersection
1896 
1897  if ( !fFullThetaSphere )
1898  {
1899  // Intersection with theta surfaces
1900  //
1901  // Known failure cases:
1902  // o Inside tolerance of stheta surface, skim
1903  // ~parallel to cone and Hit & enter etheta surface [& visa versa]
1904  //
1905  // To solve: Check 2nd root of etheta surface in addition to stheta
1906  //
1907  // o start/end theta is exactly pi/2
1908  //
1909  // Intersections with cones
1910  //
1911  // Cone equation: x^2+y^2=z^2tan^2(t)
1912  //
1913  // => (px+svx)^2+(py+svy)^2=(pz+svz)^2tan^2(t)
1914  //
1915  // => (px^2+py^2-pz^2tan^2(t))+2sd(pxvx+pyvy-pzvztan^2(t))
1916  // + sd^2(vx^2+vy^2-vz^2tan^2(t)) = 0
1917  //
1918  // => sd^2(1-vz^2(1+tan^2(t))+2sd(pdotv2d-pzvztan^2(t))
1919  // + (rho2-pz^2tan^2(t)) = 0
1920  //
1921 
1922  if(fSTheta) // intersection with first cons
1923  {
1924  if( std::fabs(tanSTheta) > 5./kAngTolerance ) // kons is plane z=0
1925  {
1926  if( v.z() > 0. )
1927  {
1928  if ( std::fabs( p.z() ) <= halfRmaxTolerance )
1929  {
1930  if(calcNorm)
1931  {
1932  *validNorm = true;
1933  *n = G4ThreeVector(0.,0.,1.);
1934  }
1935  return snxt = 0 ;
1936  }
1937  stheta = -p.z()/v.z();
1938  sidetheta = kSTheta;
1939  }
1940  }
1941  else // kons is not plane
1942  {
1943  t1 = 1-v.z()*v.z()*(1+tanSTheta2);
1944  t2 = pDotV2d-p.z()*v.z()*tanSTheta2; // ~vDotN if p on cons
1945  dist2STheta = rho2-p.z()*p.z()*tanSTheta2; // t3
1946 
1947  distTheta = std::sqrt(rho2)-p.z()*tanSTheta;
1948 
1949  if( std::fabs(t1) < halfAngTolerance ) // 1st order equation,
1950  { // v parallel to kons
1951  if( v.z() > 0. )
1952  {
1953  if(std::fabs(distTheta) < halfRmaxTolerance) // p on surface
1954  {
1955  if( (fSTheta < halfpi) && (p.z() > 0.) )
1956  {
1957  if( calcNorm ) { *validNorm = false; }
1958  return snxt = 0.;
1959  }
1960  else if( (fSTheta > halfpi) && (p.z() <= 0) )
1961  {
1962  if( calcNorm )
1963  {
1964  *validNorm = true;
1965  if (rho2)
1966  {
1967  rhoSecTheta = std::sqrt(rho2*(1+tanSTheta2));
1968 
1969  *n = G4ThreeVector( p.x()/rhoSecTheta,
1970  p.y()/rhoSecTheta,
1971  std::sin(fSTheta) );
1972  }
1973  else *n = G4ThreeVector(0.,0.,1.);
1974  }
1975  return snxt = 0.;
1976  }
1977  }
1978  stheta = -0.5*dist2STheta/t2;
1979  sidetheta = kSTheta;
1980  }
1981  } // 2nd order equation, 1st root of fSTheta cone,
1982  else // 2nd if 1st root -ve
1983  {
1984  if( std::fabs(distTheta) < halfRmaxTolerance )
1985  {
1986  if( (fSTheta > halfpi) && (t2 >= 0.) ) // leave
1987  {
1988  if( calcNorm )
1989  {
1990  *validNorm = true;
1991  if (rho2)
1992  {
1993  rhoSecTheta = std::sqrt(rho2*(1+tanSTheta2));
1994 
1995  *n = G4ThreeVector( p.x()/rhoSecTheta,
1996  p.y()/rhoSecTheta,
1997  std::sin(fSTheta) );
1998  }
1999  else { *n = G4ThreeVector(0.,0.,1.); }
2000  }
2001  return snxt = 0.;
2002  }
2003  else if( (fSTheta < halfpi) && (t2 < 0.) && (p.z() >=0.) ) // leave
2004  {
2005  if( calcNorm ) { *validNorm = false; }
2006  return snxt = 0.;
2007  }
2008  }
2009  b = t2/t1;
2010  c = dist2STheta/t1;
2011  d2 = b*b - c ;
2012 
2013  if ( d2 >= 0. )
2014  {
2015  d = std::sqrt(d2);
2016 
2017  if( fSTheta > halfpi )
2018  {
2019  sd = -b - d; // First root
2020 
2021  if ( ((std::fabs(s) < halfRmaxTolerance) && (t2 < 0.))
2022  || (sd < 0.) || ( (sd > 0.) && (p.z() + sd*v.z() > 0.) ) )
2023  {
2024  sd = -b + d ; // 2nd root
2025  }
2026  if( (sd > halfRmaxTolerance) && (p.z() + sd*v.z() <= 0.) )
2027  {
2028  stheta = sd;
2029  sidetheta = kSTheta;
2030  }
2031  }
2032  else // sTheta < pi/2, concave surface, no normal
2033  {
2034  sd = -b - d; // First root
2035 
2036  if ( ( (std::fabs(sd) < halfRmaxTolerance) && (t2 >= 0.) )
2037  || (sd < 0.) || ( (sd > 0.) && (p.z() + sd*v.z() < 0.) ) )
2038  {
2039  sd = -b + d ; // 2nd root
2040  }
2041  if( (sd > halfRmaxTolerance) && (p.z() + sd*v.z() >= 0.) )
2042  {
2043  stheta = sd;
2044  sidetheta = kSTheta;
2045  }
2046  }
2047  }
2048  }
2049  }
2050  }
2051  if (eTheta < pi) // intersection with second cons
2052  {
2053  if( std::fabs(tanETheta) > 5./kAngTolerance ) // kons is plane z=0
2054  {
2055  if( v.z() < 0. )
2056  {
2057  if ( std::fabs( p.z() ) <= halfRmaxTolerance )
2058  {
2059  if(calcNorm)
2060  {
2061  *validNorm = true;
2062  *n = G4ThreeVector(0.,0.,-1.);
2063  }
2064  return snxt = 0 ;
2065  }
2066  sd = -p.z()/v.z();
2067 
2068  if( sd < stheta )
2069  {
2070  stheta = sd;
2071  sidetheta = kETheta;
2072  }
2073  }
2074  }
2075  else // kons is not plane
2076  {
2077  t1 = 1-v.z()*v.z()*(1+tanETheta2);
2078  t2 = pDotV2d-p.z()*v.z()*tanETheta2; // ~vDotN if p on cons
2079  dist2ETheta = rho2-p.z()*p.z()*tanETheta2; // t3
2080 
2081  distTheta = std::sqrt(rho2)-p.z()*tanETheta;
2082 
2083  if( std::fabs(t1) < halfAngTolerance ) // 1st order equation,
2084  { // v parallel to kons
2085  if( v.z() < 0. )
2086  {
2087  if(std::fabs(distTheta) < halfRmaxTolerance) // p on surface
2088  {
2089  if( (eTheta > halfpi) && (p.z() < 0.) )
2090  {
2091  if( calcNorm ) { *validNorm = false; }
2092  return snxt = 0.;
2093  }
2094  else if ( (eTheta < halfpi) && (p.z() >= 0) )
2095  {
2096  if( calcNorm )
2097  {
2098  *validNorm = true;
2099  if (rho2)
2100  {
2101  rhoSecTheta = std::sqrt(rho2*(1+tanETheta2));
2102  *n = G4ThreeVector( p.x()/rhoSecTheta,
2103  p.y()/rhoSecTheta,
2104  -sinETheta );
2105  }
2106  else { *n = G4ThreeVector(0.,0.,-1.); }
2107  }
2108  return snxt = 0.;
2109  }
2110  }
2111  sd = -0.5*dist2ETheta/t2;
2112 
2113  if( sd < stheta )
2114  {
2115  stheta = sd;
2116  sidetheta = kETheta;
2117  }
2118  }
2119  } // 2nd order equation, 1st root of fSTheta cone
2120  else // 2nd if 1st root -ve
2121  {
2122  if ( std::fabs(distTheta) < halfRmaxTolerance )
2123  {
2124  if( (eTheta < halfpi) && (t2 >= 0.) ) // leave
2125  {
2126  if( calcNorm )
2127  {
2128  *validNorm = true;
2129  if (rho2)
2130  {
2131  rhoSecTheta = std::sqrt(rho2*(1+tanETheta2));
2132  *n = G4ThreeVector( p.x()/rhoSecTheta,
2133  p.y()/rhoSecTheta,
2134  -sinETheta );
2135  }
2136  else *n = G4ThreeVector(0.,0.,-1.);
2137  }
2138  return snxt = 0.;
2139  }
2140  else if ( (eTheta > halfpi)
2141  && (t2 < 0.) && (p.z() <=0.) ) // leave
2142  {
2143  if( calcNorm ) { *validNorm = false; }
2144  return snxt = 0.;
2145  }
2146  }
2147  b = t2/t1;
2148  c = dist2ETheta/t1;
2149  d2 = b*b - c ;
2150  if ( (d2 <halfRmaxTolerance) && (d2 > -halfRmaxTolerance) )
2151  {
2152  d2 = 0.;
2153  }
2154  if ( d2 >= 0. )
2155  {
2156  d = std::sqrt(d2);
2157 
2158  if( eTheta < halfpi )
2159  {
2160  sd = -b - d; // First root
2161 
2162  if( ((std::fabs(sd) < halfRmaxTolerance) && (t2 < 0.))
2163  || (sd < 0.) )
2164  {
2165  sd = -b + d ; // 2nd root
2166  }
2167  if( sd > halfRmaxTolerance )
2168  {
2169  if( sd < stheta )
2170  {
2171  stheta = sd;
2172  sidetheta = kETheta;
2173  }
2174  }
2175  }
2176  else // sTheta+fDTheta > pi/2, concave surface, no normal
2177  {
2178  sd = -b - d; // First root
2179 
2180  if ( ((std::fabs(sd) < halfRmaxTolerance) && (t2 >= 0.))
2181  || (sd < 0.)
2182  || ( (sd > 0.) && (p.z() + sd*v.z() > halfRmaxTolerance) ) )
2183  {
2184  sd = -b + d ; // 2nd root
2185  }
2186  if ( ( sd>halfRmaxTolerance )
2187  && ( p.z()+sd*v.z() <= halfRmaxTolerance ) )
2188  {
2189  if( sd < stheta )
2190  {
2191  stheta = sd;
2192  sidetheta = kETheta;
2193  }
2194  }
2195  }
2196  }
2197  }
2198  }
2199  }
2200 
2201  } // end theta intersections
2202 
2203  // Phi Intersection
2204 
2205  if ( !fFullPhiSphere )
2206  {
2207  if ( p.x() || p.y() ) // Check if on z axis (rho not needed later)
2208  {
2209  // pDist -ve when inside
2210 
2211  pDistS=p.x()*sinSPhi-p.y()*cosSPhi;
2212  pDistE=-p.x()*sinEPhi+p.y()*cosEPhi;
2213 
2214  // Comp -ve when in direction of outwards normal
2215 
2216  compS = -sinSPhi*v.x()+cosSPhi*v.y() ;
2217  compE = sinEPhi*v.x()-cosEPhi*v.y() ;
2218  sidephi = kNull ;
2219 
2220  if ( (pDistS <= 0) && (pDistE <= 0) )
2221  {
2222  // Inside both phi *full* planes
2223 
2224  if ( compS < 0 )
2225  {
2226  sphi = pDistS/compS ;
2227  xi = p.x()+sphi*v.x() ;
2228  yi = p.y()+sphi*v.y() ;
2229 
2230  // Check intersection with correct half-plane (if not -> no intersect)
2231  //
2232  if( (std::fabs(xi)<=kCarTolerance) && (std::fabs(yi)<=kCarTolerance) )
2233  {
2234  vphi = std::atan2(v.y(),v.x());
2235  sidephi = kSPhi;
2236  if ( ( (fSPhi-halfAngTolerance) <= vphi)
2237  && ( (ePhi+halfAngTolerance) >= vphi) )
2238  {
2239  sphi = kInfinity;
2240  }
2241  }
2242  else if ( ( yi*cosCPhi - xi*sinCPhi ) >= 0 )
2243  {
2244  sphi=kInfinity;
2245  }
2246  else
2247  {
2248  sidephi = kSPhi ;
2249  if ( pDistS > -halfCarTolerance) { sphi = 0; } // Leave by sphi
2250  }
2251  }
2252  else { sphi = kInfinity; }
2253 
2254  if ( compE < 0 )
2255  {
2256  sphi2=pDistE/compE ;
2257  if (sphi2 < sphi) // Only check further if < starting phi intersection
2258  {
2259  xi = p.x()+sphi2*v.x() ;
2260  yi = p.y()+sphi2*v.y() ;
2261 
2262  // Check intersection with correct half-plane
2263  //
2264  if ( (std::fabs(xi)<=kCarTolerance)
2265  && (std::fabs(yi)<=kCarTolerance))
2266  {
2267  // Leaving via ending phi
2268  //
2269  vphi = std::atan2(v.y(),v.x()) ;
2270 
2271  if( !((fSPhi-halfAngTolerance <= vphi)
2272  &&(fSPhi+fDPhi+halfAngTolerance >= vphi)) )
2273  {
2274  sidephi = kEPhi;
2275  if ( pDistE <= -halfCarTolerance ) { sphi = sphi2; }
2276  else { sphi = 0.0; }
2277  }
2278  }
2279  else if ((yi*cosCPhi-xi*sinCPhi)>=0) // Leaving via ending phi
2280  {
2281  sidephi = kEPhi ;
2282  if ( pDistE <= -halfCarTolerance )
2283  {
2284  sphi=sphi2;
2285  }
2286  else
2287  {
2288  sphi = 0 ;
2289  }
2290  }
2291  }
2292  }
2293  }
2294  else if ((pDistS >= 0) && (pDistE >= 0)) // Outside both *full* phi planes
2295  {
2296  if ( pDistS <= pDistE )
2297  {
2298  sidephi = kSPhi ;
2299  }
2300  else
2301  {
2302  sidephi = kEPhi ;
2303  }
2304  if ( fDPhi > pi )
2305  {
2306  if ( (compS < 0) && (compE < 0) ) { sphi = 0; }
2307  else { sphi = kInfinity; }
2308  }
2309  else
2310  {
2311  // if towards both >=0 then once inside (after error)
2312  // will remain inside
2313 
2314  if ( (compS >= 0) && (compE >= 0) ) { sphi = kInfinity; }
2315  else { sphi = 0; }
2316  }
2317  }
2318  else if ( (pDistS > 0) && (pDistE < 0) )
2319  {
2320  // Outside full starting plane, inside full ending plane
2321 
2322  if ( fDPhi > pi )
2323  {
2324  if ( compE < 0 )
2325  {
2326  sphi = pDistE/compE ;
2327  xi = p.x() + sphi*v.x() ;
2328  yi = p.y() + sphi*v.y() ;
2329 
2330  // Check intersection in correct half-plane
2331  // (if not -> not leaving phi extent)
2332  //
2333  if( (std::fabs(xi)<=kCarTolerance)&&(std::fabs(yi)<=kCarTolerance) )
2334  {
2335  vphi = std::atan2(v.y(),v.x());
2336  sidephi = kSPhi;
2337  if ( ( (fSPhi-halfAngTolerance) <= vphi)
2338  && ( (ePhi+halfAngTolerance) >= vphi) )
2339  {
2340  sphi = kInfinity;
2341  }
2342  }
2343  else if ( ( yi*cosCPhi - xi*sinCPhi ) <= 0 )
2344  {
2345  sphi = kInfinity ;
2346  }
2347  else // Leaving via Ending phi
2348  {
2349  sidephi = kEPhi ;
2350  if ( pDistE > -halfCarTolerance ) { sphi = 0.; }
2351  }
2352  }
2353  else
2354  {
2355  sphi = kInfinity ;
2356  }
2357  }
2358  else
2359  {
2360  if ( compS >= 0 )
2361  {
2362  if ( compE < 0 )
2363  {
2364  sphi = pDistE/compE ;
2365  xi = p.x() + sphi*v.x() ;
2366  yi = p.y() + sphi*v.y() ;
2367 
2368  // Check intersection in correct half-plane
2369  // (if not -> remain in extent)
2370  //
2371  if( (std::fabs(xi)<=kCarTolerance)
2372  && (std::fabs(yi)<=kCarTolerance) )
2373  {
2374  vphi = std::atan2(v.y(),v.x());
2375  sidephi = kSPhi;
2376  if ( ( (fSPhi-halfAngTolerance) <= vphi)
2377  && ( (ePhi+halfAngTolerance) >= vphi) )
2378  {
2379  sphi = kInfinity;
2380  }
2381  }
2382  else if ( ( yi*cosCPhi - xi*sinCPhi) <= 0 )
2383  {
2384  sphi=kInfinity;
2385  }
2386  else // otherwise leaving via Ending phi
2387  {
2388  sidephi = kEPhi ;
2389  }
2390  }
2391  else sphi=kInfinity;
2392  }
2393  else // leaving immediately by starting phi
2394  {
2395  sidephi = kSPhi ;
2396  sphi = 0 ;
2397  }
2398  }
2399  }
2400  else
2401  {
2402  // Must be pDistS < 0 && pDistE > 0
2403  // Inside full starting plane, outside full ending plane
2404 
2405  if ( fDPhi > pi )
2406  {
2407  if ( compS < 0 )
2408  {
2409  sphi=pDistS/compS;
2410  xi=p.x()+sphi*v.x();
2411  yi=p.y()+sphi*v.y();
2412 
2413  // Check intersection in correct half-plane
2414  // (if not -> not leaving phi extent)
2415  //
2416  if( (std::fabs(xi)<=kCarTolerance)&&(std::fabs(yi)<=kCarTolerance) )
2417  {
2418  vphi = std::atan2(v.y(),v.x()) ;
2419  sidephi = kSPhi;
2420  if ( ( (fSPhi-halfAngTolerance) <= vphi)
2421  && ( (ePhi+halfAngTolerance) >= vphi) )
2422  {
2423  sphi = kInfinity;
2424  }
2425  }
2426  else if ( ( yi*cosCPhi - xi*sinCPhi ) >= 0 )
2427  {
2428  sphi = kInfinity ;
2429  }
2430  else // Leaving via Starting phi
2431  {
2432  sidephi = kSPhi ;
2433  if ( pDistS > -halfCarTolerance ) { sphi = 0; }
2434  }
2435  }
2436  else
2437  {
2438  sphi = kInfinity ;
2439  }
2440  }
2441  else
2442  {
2443  if ( compE >= 0 )
2444  {
2445  if ( compS < 0 )
2446  {
2447  sphi = pDistS/compS ;
2448  xi = p.x()+sphi*v.x() ;
2449  yi = p.y()+sphi*v.y() ;
2450 
2451  // Check intersection in correct half-plane
2452  // (if not -> remain in extent)
2453  //
2454  if( (std::fabs(xi)<=kCarTolerance)
2455  && (std::fabs(yi)<=kCarTolerance))
2456  {
2457  vphi = std::atan2(v.y(),v.x()) ;
2458  sidephi = kSPhi;
2459  if ( ( (fSPhi-halfAngTolerance) <= vphi)
2460  && ( (ePhi+halfAngTolerance) >= vphi) )
2461  {
2462  sphi = kInfinity;
2463  }
2464  }
2465  else if ( ( yi*cosCPhi - xi*sinCPhi ) >= 0 )
2466  {
2467  sphi = kInfinity ;
2468  }
2469  else // otherwise leaving via Starting phi
2470  {
2471  sidephi = kSPhi ;
2472  }
2473  }
2474  else
2475  {
2476  sphi = kInfinity ;
2477  }
2478  }
2479  else // leaving immediately by ending
2480  {
2481  sidephi = kEPhi ;
2482  sphi = 0 ;
2483  }
2484  }
2485  }
2486  }
2487  else
2488  {
2489  // On z axis + travel not || to z axis -> if phi of vector direction
2490  // within phi of shape, Step limited by rmax, else Step =0
2491 
2492  if ( v.x() || v.y() )
2493  {
2494  vphi = std::atan2(v.y(),v.x()) ;
2495  if ((fSPhi-halfAngTolerance < vphi) && (vphi < ePhi+halfAngTolerance))
2496  {
2497  sphi = kInfinity;
2498  }
2499  else
2500  {
2501  sidephi = kSPhi ; // arbitrary
2502  sphi = 0 ;
2503  }
2504  }
2505  else // travel along z - no phi intersection
2506  {
2507  sphi = kInfinity ;
2508  }
2509  }
2510  if ( sphi < snxt ) // Order intersecttions
2511  {
2512  snxt = sphi ;
2513  side = sidephi ;
2514  }
2515  }
2516  if (stheta < snxt ) // Order intersections
2517  {
2518  snxt = stheta ;
2519  side = sidetheta ;
2520  }
2521 
2522  if (calcNorm) // Output switch operator
2523  {
2524  switch( side )
2525  {
2526  case kRMax:
2527  xi=p.x()+snxt*v.x();
2528  yi=p.y()+snxt*v.y();
2529  zi=p.z()+snxt*v.z();
2530  *n=G4ThreeVector(xi/fRmax,yi/fRmax,zi/fRmax);
2531  *validNorm=true;
2532  break;
2533 
2534  case kRMin:
2535  *validNorm=false; // Rmin is concave
2536  break;
2537 
2538  case kSPhi:
2539  if ( fDPhi <= pi ) // Normal to Phi-
2540  {
2541  *n=G4ThreeVector(sinSPhi,-cosSPhi,0);
2542  *validNorm=true;
2543  }
2544  else { *validNorm=false; }
2545  break ;
2546 
2547  case kEPhi:
2548  if ( fDPhi <= pi ) // Normal to Phi+
2549  {
2550  *n=G4ThreeVector(-sinEPhi,cosEPhi,0);
2551  *validNorm=true;
2552  }
2553  else { *validNorm=false; }
2554  break;
2555 
2556  case kSTheta:
2557  if( fSTheta == halfpi )
2558  {
2559  *n=G4ThreeVector(0.,0.,1.);
2560  *validNorm=true;
2561  }
2562  else if ( fSTheta > halfpi )
2563  {
2564  xi = p.x() + snxt*v.x();
2565  yi = p.y() + snxt*v.y();
2566  rho2=xi*xi+yi*yi;
2567  if (rho2)
2568  {
2569  rhoSecTheta = std::sqrt(rho2*(1+tanSTheta2));
2570  *n = G4ThreeVector( xi/rhoSecTheta, yi/rhoSecTheta,
2571  -tanSTheta/std::sqrt(1+tanSTheta2));
2572  }
2573  else
2574  {
2575  *n = G4ThreeVector(0.,0.,1.);
2576  }
2577  *validNorm=true;
2578  }
2579  else { *validNorm=false; } // Concave STheta cone
2580  break;
2581 
2582  case kETheta:
2583  if( eTheta == halfpi )
2584  {
2585  *n = G4ThreeVector(0.,0.,-1.);
2586  *validNorm = true;
2587  }
2588  else if ( eTheta < halfpi )
2589  {
2590  xi=p.x()+snxt*v.x();
2591  yi=p.y()+snxt*v.y();
2592  rho2=xi*xi+yi*yi;
2593  if (rho2)
2594  {
2595  rhoSecTheta = std::sqrt(rho2*(1+tanETheta2));
2596  *n = G4ThreeVector( xi/rhoSecTheta, yi/rhoSecTheta,
2597  -tanETheta/std::sqrt(1+tanETheta2) );
2598  }
2599  else
2600  {
2601  *n = G4ThreeVector(0.,0.,-1.);
2602  }
2603  *validNorm=true;
2604  }
2605  else { *validNorm=false; } // Concave ETheta cone
2606  break;
2607 
2608  default:
2609  G4cout << G4endl;
2610  DumpInfo();
2611  std::ostringstream message;
2612  G4int oldprc = message.precision(16);
2613  message << "Undefined side for valid surface normal to solid."
2614  << G4endl
2615  << "Position:" << G4endl << G4endl
2616  << "p.x() = " << p.x()/mm << " mm" << G4endl
2617  << "p.y() = " << p.y()/mm << " mm" << G4endl
2618  << "p.z() = " << p.z()/mm << " mm" << G4endl << G4endl
2619  << "Direction:" << G4endl << G4endl
2620  << "v.x() = " << v.x() << G4endl
2621  << "v.y() = " << v.y() << G4endl
2622  << "v.z() = " << v.z() << G4endl << G4endl
2623  << "Proposed distance :" << G4endl << G4endl
2624  << "snxt = " << snxt/mm << " mm" << G4endl;
2625  message.precision(oldprc);
2626  G4Exception("G4Sphere::DistanceToOut(p,v,..)",
2627  "GeomSolids1002", JustWarning, message);
2628  break;
2629  }
2630  }
2631  if (snxt == kInfinity)
2632  {
2633  G4cout << G4endl;
2634  DumpInfo();
2635  std::ostringstream message;
2636  G4int oldprc = message.precision(16);
2637  message << "Logic error: snxt = kInfinity ???" << G4endl
2638  << "Position:" << G4endl << G4endl
2639  << "p.x() = " << p.x()/mm << " mm" << G4endl
2640  << "p.y() = " << p.y()/mm << " mm" << G4endl
2641  << "p.z() = " << p.z()/mm << " mm" << G4endl << G4endl
2642  << "Rp = "<< std::sqrt( p.x()*p.x()+p.y()*p.y()+p.z()*p.z() )/mm
2643  << " mm" << G4endl << G4endl
2644  << "Direction:" << G4endl << G4endl
2645  << "v.x() = " << v.x() << G4endl
2646  << "v.y() = " << v.y() << G4endl
2647  << "v.z() = " << v.z() << G4endl << G4endl
2648  << "Proposed distance :" << G4endl << G4endl
2649  << "snxt = " << snxt/mm << " mm" << G4endl;
2650  message.precision(oldprc);
2651  G4Exception("G4Sphere::DistanceToOut(p,v,..)",
2652  "GeomSolids1002", JustWarning, message);
2653  }
2654 
2655  return snxt;
2656 }
mm
static constexpr double mm
Definition: G4SIunits.hh:115
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
CLHEP::Hep3Vector::x
double x() const
d2
static const G4double d2
Definition: G4ElectroNuclearCrossSection.cc:89
JustWarning
Definition: G4ExceptionSeverity.hh:64
G4int
int G4int
Definition: G4Types.hh:78
CLHEP::Hep3Vector::z
double z() const
G4VSolid::DumpInfo
void DumpInfo() const
s
const XML_Char * s
Definition: expat.h:262
test.b
tuple b
Definition: test.py:12
G4cout
G4GLOB_DLL std::ostream G4cout
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
plottest35.t1
tuple t1
Definition: plottest35.py:33
CLHEP::Hep3Vector::y
double y() const
G4endl
#define G4endl
Definition: G4ios.hh:61
G4VSolid::kCarTolerance
G4double kCarTolerance
Definition: G4VSolid.hh:307
pi
static constexpr double pi
Definition: G4SIunits.hh:75
halfpi
static constexpr double halfpi
Definition: G4SIunits.hh:77
ESide
ESide
Definition: G4Cons.cc:76
G4double
double G4double
Definition: G4Types.hh:76
test.c
tuple c
Definition: test.py:13

Here is the call graph for this function:

G4double G4Sphere::DistanceToOut ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 2662 of file G4Sphere.cc.

2663 {
2664  G4double safe=0.0,safeRMin,safeRMax,safePhi,safeTheta;
2665  G4double rho2,rds,rho;
2666  G4double pTheta,dTheta1 = kInfinity,dTheta2 = kInfinity;
2667  rho2=p.x()*p.x()+p.y()*p.y();
2668  rds=std::sqrt(rho2+p.z()*p.z());
2669  rho=std::sqrt(rho2);
2670 
2671 #ifdef G4CSGDEBUG
2672  if( Inside(p) == kOutside )
2673  {
2674  G4int old_prc = G4cout.precision(16);
2675  G4cout << G4endl;
2676  DumpInfo();
2677  G4cout << "Position:" << G4endl << G4endl ;
2678  G4cout << "p.x() = " << p.x()/mm << " mm" << G4endl ;
2679  G4cout << "p.y() = " << p.y()/mm << " mm" << G4endl ;
2680  G4cout << "p.z() = " << p.z()/mm << " mm" << G4endl << G4endl ;
2681  G4cout.precision(old_prc) ;
2682  G4Exception("G4Sphere::DistanceToOut(p)",
2683  "GeomSolids1002", JustWarning, "Point p is outside !?" );
2684  }
2685 #endif
2686 
2687  // Distance to r shells
2688  //
2689  safeRMax = fRmax-rds;
2690  safe = safeRMax;
2691  if (fRmin)
2692  {
2693  safeRMin = rds-fRmin;
2694  safe = std::min( safeRMin, safeRMax );
2695  }
2696 
2697  // Distance to phi extent
2698  //
2699  if ( !fFullPhiSphere )
2700  {
2701  if (rho>0.0)
2702  {
2703  if ((p.y()*cosCPhi-p.x()*sinCPhi)<=0)
2704  {
2705  safePhi=-(p.x()*sinSPhi-p.y()*cosSPhi);
2706  }
2707  else
2708  {
2709  safePhi=(p.x()*sinEPhi-p.y()*cosEPhi);
2710  }
2711  }
2712  else
2713  {
2714  safePhi = 0.0; // Distance to both Phi surfaces (extended)
2715  }
2716  // Both cases above can be improved - in case fRMin > 0.0
2717  // although it may be costlier (good for precise, not fast version)
2718 
2719  safe= std::min(safe, safePhi);
2720  }
2721 
2722  // Distance to Theta extent
2723  //
2724  if ( !fFullThetaSphere )
2725  {
2726  if( rds > 0.0 )
2727  {
2728  pTheta=std::acos(p.z()/rds);
2729  if (pTheta<0) { pTheta+=pi; }
2730  if(fSTheta>0.)
2731  { dTheta1=pTheta-fSTheta;}
2732  if(eTheta<pi)
2733  { dTheta2=eTheta-pTheta;}
2734 
2735  safeTheta=rds*std::sin(std::min(dTheta1, dTheta2) );
2736  }
2737  else
2738  {
2739  safeTheta= 0.0;
2740  // An improvement will be to return negative answer if outside (TODO)
2741  }
2742  safe = std::min( safe, safeTheta );
2743  }
2744 
2745  if (safe<0.0) { safe=0; }
2746  // An improvement to return negative answer if outside (TODO)
2747 
2748  return safe;
2749 }
mm
static constexpr double mm
Definition: G4SIunits.hh:115
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
CLHEP::Hep3Vector::x
double x() const
JustWarning
Definition: G4ExceptionSeverity.hh:64
G4int
int G4int
Definition: G4Types.hh:78
CLHEP::Hep3Vector::z
double z() const
G4VSolid::DumpInfo
void DumpInfo() const
G4cout
G4GLOB_DLL std::ostream G4cout
G4Sphere::Inside
EInside Inside(const G4ThreeVector &p) const
Definition: G4Sphere.cc:310
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
CLHEP::Hep3Vector::y
double y() const
G4INCL::Math::min
T min(const T t1, const T t2)
brief Return the smallest of the two arguments
Definition: G4INCLGlobals.hh:117
G4endl
#define G4endl
Definition: G4ios.hh:61
pi
static constexpr double pi
Definition: G4SIunits.hh:75
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

void G4Sphere::Extent ( G4ThreeVector &  pMin,
G4ThreeVector &  pMax 
) const
virtual

Reimplemented from G4VSolid.

Definition at line 233 of file G4Sphere.cc.

234 {
235  G4double rmin = GetInnerRadius();
236  G4double rmax = GetOuterRadius();
237 
238  // Find bounding box
239  //
240  if (GetDeltaThetaAngle() >= pi && GetDeltaPhiAngle() >= twopi)
241  {
242  pMin.set(-rmax,-rmax,-rmax);
243  pMax.set( rmax, rmax, rmax);
244  }
245  else
246  {
247  G4double sinStart = GetSinStartTheta();
248  G4double cosStart = GetCosStartTheta();
249  G4double sinEnd = GetSinEndTheta();
250  G4double cosEnd = GetCosEndTheta();
251 
252  G4double stheta = GetStartThetaAngle();
253  G4double etheta = stheta + GetDeltaThetaAngle();
254  G4double rhomin = rmin*std::min(sinStart,sinEnd);
255  G4double rhomax = rmax;
256  if (stheta > halfpi) rhomax = rmax*sinStart;
257  if (etheta < halfpi) rhomax = rmax*sinEnd;
258 
259  G4TwoVector xymin,xymax;
260  G4GeomTools::DiskExtent(rhomin,rhomax,
261  GetSinStartPhi(),GetCosStartPhi(),
262  GetSinEndPhi(),GetCosEndPhi(),
263  xymin,xymax);
264 
265  G4double zmin = std::min(rmin*cosEnd,rmax*cosEnd);
266  G4double zmax = std::max(rmin*cosStart,rmax*cosStart);
267  pMin.set(xymin.x(),xymin.y(),zmin);
268  pMax.set(xymax.x(),xymax.y(),zmax);
269  }
270 
271  // Check correctness of the bounding box
272  //
273  if (pMin.x() >= pMax.x() || pMin.y() >= pMax.y() || pMin.z() >= pMax.z())
274  {
275  std::ostringstream message;
276  message << "Bad bounding box (min >= max) for solid: "
277  << GetName() << " !"
278  << "\npMin = " << pMin
279  << "\npMax = " << pMax;
280  G4Exception("G4Sphere::Extent()", "GeomMgt0001", JustWarning, message);
281  DumpInfo();
282  }
283 }
CLHEP::Hep3Vector::set
void set(double x, double y, double z)
G4VSolid::GetName
G4String GetName() const
G4Sphere::GetCosStartTheta
G4double GetCosStartTheta() const
CLHEP::Hep2Vector::y
double y() const
CLHEP::Hep2Vector::x
double x() const
G4Sphere::GetSinStartPhi
G4double GetSinStartPhi() const
CLHEP::Hep3Vector::x
double x() const
G4Sphere::GetCosEndTheta
G4double GetCosEndTheta() const
G4Sphere::GetSinEndTheta
G4double GetSinEndTheta() const
G4Sphere::GetSinStartTheta
G4double GetSinStartTheta() const
G4Sphere::GetDeltaPhiAngle
G4double GetDeltaPhiAngle() const
JustWarning
Definition: G4ExceptionSeverity.hh:64
CLHEP::Hep3Vector::z
double z() const
G4VSolid::DumpInfo
void DumpInfo() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4Sphere::GetStartThetaAngle
G4double GetStartThetaAngle() const
G4Sphere::GetInnerRadius
G4double GetInnerRadius() const
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
G4INCL::Math::max
T max(const T t1, const T t2)
brief Return the largest of the two arguments
Definition: G4INCLGlobals.hh:112
CLHEP::Hep3Vector::y
double y() const
G4INCL::Math::min
T min(const T t1, const T t2)
brief Return the smallest of the two arguments
Definition: G4INCLGlobals.hh:117
G4Sphere::GetCosStartPhi
G4double GetCosStartPhi() const
G4Sphere::GetSinEndPhi
G4double GetSinEndPhi() const
pi
static constexpr double pi
Definition: G4SIunits.hh:75
halfpi
static constexpr double halfpi
Definition: G4SIunits.hh:77
G4Sphere::GetOuterRadius
G4double GetOuterRadius() const
G4double
double G4double
Definition: G4Types.hh:76
G4Sphere::GetDeltaThetaAngle
G4double GetDeltaThetaAngle() const
G4GeomTools::DiskExtent
static G4bool DiskExtent(G4double rmin, G4double rmax, G4double startPhi, G4double delPhi, G4TwoVector &pmin, G4TwoVector &pmax)
Definition: G4GeomTools.cc:378
G4Sphere::GetCosEndPhi
G4double GetCosEndPhi() const

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Sphere::GetCosEndPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetCosEndTheta ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetCosStartPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetCosStartTheta ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetCubicVolume ( )
inlinevirtual

Reimplemented from G4VSolid.

G4double G4Sphere::GetDeltaPhiAngle ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetDeltaThetaAngle ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetDPhi ( ) const
inline
G4double G4Sphere::GetDTheta ( ) const
inline
G4GeometryType G4Sphere::GetEntityType ( ) const
virtual

Implements G4VSolid.

Definition at line 2755 of file G4Sphere.cc.

2756 {
2757  return G4String("G4Sphere");
2758 }
G4VisExtent G4Sphere::GetExtent ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2926 of file G4Sphere.cc.

2927 {
2928  return G4VisExtent(-fRmax, fRmax,-fRmax, fRmax,-fRmax, fRmax );
2929 }
G4double G4Sphere::GetInnerRadius ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetInsideRadius ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetOuterRadius ( ) const
inline

Here is the caller graph for this function:

G4ThreeVector G4Sphere::GetPointOnSurface ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2797 of file G4Sphere.cc.

2798 {
2799  G4double zRand, aOne, aTwo, aThr, aFou, aFiv, chose, phi, sinphi, cosphi;
2800  G4double height1, height2, slant1, slant2, costheta, sintheta, rRand;
2801 
2802  height1 = (fRmax-fRmin)*cosSTheta;
2803  height2 = (fRmax-fRmin)*cosETheta;
2804  slant1 = std::sqrt(sqr((fRmax - fRmin)*sinSTheta) + height1*height1);
2805  slant2 = std::sqrt(sqr((fRmax - fRmin)*sinETheta) + height2*height2);
2806  rRand = GetRadiusInRing(fRmin,fRmax);
2807 
2808  aOne = fRmax*fRmax*fDPhi*(cosSTheta-cosETheta);
2809  aTwo = fRmin*fRmin*fDPhi*(cosSTheta-cosETheta);
2810  aThr = fDPhi*((fRmax + fRmin)*sinSTheta)*slant1;
2811  aFou = fDPhi*((fRmax + fRmin)*sinETheta)*slant2;
2812  aFiv = 0.5*fDTheta*(fRmax*fRmax-fRmin*fRmin);
2813 
2814  phi = G4RandFlat::shoot(fSPhi, ePhi);
2815  cosphi = std::cos(phi);
2816  sinphi = std::sin(phi);
2817  costheta = G4RandFlat::shoot(cosETheta,cosSTheta);
2818  sintheta = std::sqrt(1.-sqr(costheta));
2819 
2820  if(fFullPhiSphere) { aFiv = 0; }
2821  if(fSTheta == 0) { aThr=0; }
2822  if(eTheta == pi) { aFou = 0; }
2823  if(fSTheta == halfpi) { aThr = pi*(fRmax*fRmax-fRmin*fRmin); }
2824  if(eTheta == halfpi) { aFou = pi*(fRmax*fRmax-fRmin*fRmin); }
2825 
2826  chose = G4RandFlat::shoot(0.,aOne+aTwo+aThr+aFou+2.*aFiv);
2827  if( (chose>=0.) && (chose<aOne) )
2828  {
2829  return G4ThreeVector(fRmax*sintheta*cosphi,
2830  fRmax*sintheta*sinphi, fRmax*costheta);
2831  }
2832  else if( (chose>=aOne) && (chose<aOne+aTwo) )
2833  {
2834  return G4ThreeVector(fRmin*sintheta*cosphi,
2835  fRmin*sintheta*sinphi, fRmin*costheta);
2836  }
2837  else if( (chose>=aOne+aTwo) && (chose<aOne+aTwo+aThr) )
2838  {
2839  if (fSTheta != halfpi)
2840  {
2841  zRand = G4RandFlat::shoot(fRmin*cosSTheta,fRmax*cosSTheta);
2842  return G4ThreeVector(tanSTheta*zRand*cosphi,
2843  tanSTheta*zRand*sinphi,zRand);
2844  }
2845  else
2846  {
2847  return G4ThreeVector(rRand*cosphi, rRand*sinphi, 0.);
2848  }
2849  }
2850  else if( (chose>=aOne+aTwo+aThr) && (chose<aOne+aTwo+aThr+aFou) )
2851  {
2852  if(eTheta != halfpi)
2853  {
2854  zRand = G4RandFlat::shoot(fRmin*cosETheta, fRmax*cosETheta);
2855  return G4ThreeVector (tanETheta*zRand*cosphi,
2856  tanETheta*zRand*sinphi,zRand);
2857  }
2858  else
2859  {
2860  return G4ThreeVector(rRand*cosphi, rRand*sinphi, 0.);
2861  }
2862  }
2863  else if( (chose>=aOne+aTwo+aThr+aFou) && (chose<aOne+aTwo+aThr+aFou+aFiv) )
2864  {
2865  return G4ThreeVector(rRand*sintheta*cosSPhi,
2866  rRand*sintheta*sinSPhi,rRand*costheta);
2867  }
2868  else
2869  {
2870  return G4ThreeVector(rRand*sintheta*cosEPhi,
2871  rRand*sintheta*sinEPhi,rRand*costheta);
2872  }
2873 }
G4INCL::DeJongSpin::shoot
ThreeVector shoot(const G4int Ap, const G4int Af)
Definition: G4INCLDeJongSpin.cc:68
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
G4CSGSolid::GetRadiusInRing
G4double GetRadiusInRing(G4double rmin, G4double rmax) const
Definition: G4CSGSolid.cc:111
pi
static constexpr double pi
Definition: G4SIunits.hh:75
halfpi
static constexpr double halfpi
Definition: G4SIunits.hh:77
sqr
T sqr(const T &x)
Definition: templates.hh:145
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

G4double G4Sphere::GetRmax ( ) const
inline
G4double G4Sphere::GetRmin ( ) const
inline
G4double G4Sphere::GetSinEndPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetSinEndTheta ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetSinStartPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetSinStartTheta ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetSPhi ( ) const
inline
G4double G4Sphere::GetStartPhiAngle ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetStartThetaAngle ( ) const
inline

Here is the caller graph for this function:

G4double G4Sphere::GetSTheta ( ) const
inline
G4double G4Sphere::GetSurfaceArea ( )
virtual

Reimplemented from G4VSolid.

Definition at line 2879 of file G4Sphere.cc.

2880 {
2881  if(fSurfaceArea != 0.) {;}
2882  else
2883  {
2884  G4double Rsq=fRmax*fRmax;
2885  G4double rsq=fRmin*fRmin;
2886 
2887  fSurfaceArea = fDPhi*(rsq+Rsq)*(cosSTheta - cosETheta);
2888  if(!fFullPhiSphere)
2889  {
2890  fSurfaceArea = fSurfaceArea + fDTheta*(Rsq-rsq);
2891  }
2892  if(fSTheta >0)
2893  {
2894  G4double acos1=std::acos( std::pow(sinSTheta,2) * std::cos(fDPhi)
2895  + std::pow(cosSTheta,2));
2896  if(fDPhi>pi)
2897  {
2898  fSurfaceArea = fSurfaceArea + 0.5*(Rsq-rsq)*(twopi-acos1);
2899  }
2900  else
2901  {
2902  fSurfaceArea = fSurfaceArea + 0.5*(Rsq-rsq)*acos1;
2903  }
2904  }
2905  if(eTheta < pi)
2906  {
2907  G4double acos2=std::acos( std::pow(sinETheta,2) * std::cos(fDPhi)
2908  + std::pow(cosETheta,2));
2909  if(fDPhi>pi)
2910  {
2911  fSurfaceArea = fSurfaceArea + 0.5*(Rsq-rsq)*(twopi-acos2);
2912  }
2913  else
2914  {
2915  fSurfaceArea = fSurfaceArea + 0.5*(Rsq-rsq)*acos2;
2916  }
2917  }
2918  }
2919  return fSurfaceArea;
2920 }
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4CSGSolid::fSurfaceArea
G4double fSurfaceArea
Definition: G4CSGSolid.hh:79
pi
static constexpr double pi
Definition: G4SIunits.hh:75
G4double
double G4double
Definition: G4Types.hh:76
EInside G4Sphere::Inside ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 310 of file G4Sphere.cc.

311 {
312  G4double rho,rho2,rad2,tolRMin,tolRMax;
313  G4double pPhi,pTheta;
314  EInside in = kOutside;
315 
316  const G4double halfRmaxTolerance = fRmaxTolerance*0.5;
317  const G4double halfRminTolerance = fRminTolerance*0.5;
318  const G4double Rmax_minus = fRmax - halfRmaxTolerance;
319  const G4double Rmin_plus = (fRmin > 0) ? fRmin+halfRminTolerance : 0;
320 
321  rho2 = p.x()*p.x() + p.y()*p.y() ;
322  rad2 = rho2 + p.z()*p.z() ;
323 
324  // Check radial surfaces. Sets 'in'
325 
326  tolRMin = Rmin_plus;
327  tolRMax = Rmax_minus;
328 
329  if(rad2 == 0.0)
330  {
331  if (fRmin > 0.0)
332  {
333  return in = kOutside;
334  }
335  if ( (!fFullPhiSphere) || (!fFullThetaSphere) )
336  {
337  return in = kSurface;
338  }
339  else
340  {
341  return in = kInside;
342  }
343  }
344 
345  if ( (rad2 <= Rmax_minus*Rmax_minus) && (rad2 >= Rmin_plus*Rmin_plus) )
346  {
347  in = kInside;
348  }
349  else
350  {
351  tolRMax = fRmax + halfRmaxTolerance; // outside case
352  tolRMin = std::max(fRmin-halfRminTolerance, 0.); // outside case
353  if ( (rad2 <= tolRMax*tolRMax) && (rad2 >= tolRMin*tolRMin) )
354  {
355  in = kSurface;
356  }
357  else
358  {
359  return in = kOutside;
360  }
361  }
362 
363  // Phi boundaries : Do not check if it has no phi boundary!
364 
365  if ( !fFullPhiSphere && rho2 ) // [fDPhi < twopi] and [p.x or p.y]
366  {
367  pPhi = std::atan2(p.y(),p.x()) ;
368 
369  if ( pPhi < fSPhi - halfAngTolerance ) { pPhi += twopi; }
370  else if ( pPhi > ePhi + halfAngTolerance ) { pPhi -= twopi; }
371 
372  if ( (pPhi < fSPhi - halfAngTolerance)
373  || (pPhi > ePhi + halfAngTolerance) ) { return in = kOutside; }
374 
375  else if (in == kInside) // else it's kSurface anyway already
376  {
377  if ( (pPhi < fSPhi + halfAngTolerance)
378  || (pPhi > ePhi - halfAngTolerance) ) { in = kSurface; }
379  }
380  }
381 
382  // Theta bondaries
383 
384  if ( (rho2 || p.z()) && (!fFullThetaSphere) )
385  {
386  rho = std::sqrt(rho2);
387  pTheta = std::atan2(rho,p.z());
388 
389  if ( in == kInside )
390  {
391  if ( ((fSTheta > 0.0) && (pTheta < fSTheta + halfAngTolerance))
392  || ((eTheta < pi) && (pTheta > eTheta - halfAngTolerance)) )
393  {
394  if ( (( (fSTheta>0.0)&&(pTheta>=fSTheta-halfAngTolerance) )
395  || (fSTheta == 0.0) )
396  && ((eTheta==pi)||(pTheta <= eTheta + halfAngTolerance) ) )
397  {
398  in = kSurface;
399  }
400  else
401  {
402  in = kOutside;
403  }
404  }
405  }
406  else
407  {
408  if ( ((fSTheta > 0.0)&&(pTheta < fSTheta - halfAngTolerance))
409  ||((eTheta < pi )&&(pTheta > eTheta + halfAngTolerance)) )
410  {
411  in = kOutside;
412  }
413  }
414  }
415  return in;
416 }
CLHEP::Hep3Vector::x
double x() const
CLHEP::Hep3Vector::z
double z() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4INCL::Math::max
T max(const T t1, const T t2)
brief Return the largest of the two arguments
Definition: G4INCLGlobals.hh:112
EInside
EInside
Definition: geomdefs.hh:58
CLHEP::Hep3Vector::y
double y() const
pi
static constexpr double pi
Definition: G4SIunits.hh:75
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

Here is the caller graph for this function:

G4Sphere & G4Sphere::operator= ( const G4Sphere &  rhs)

Definition at line 184 of file G4Sphere.cc.

185 {
186  // Check assignment to self
187  //
188  if (this == &rhs) { return *this; }
189 
190  // Copy base class data
191  //
192  G4CSGSolid::operator=(rhs);
193 
194  // Copy data
195  //
196  fRminTolerance = rhs.fRminTolerance; fRmaxTolerance = rhs.fRmaxTolerance;
197  kAngTolerance = rhs.kAngTolerance; kRadTolerance = rhs.kRadTolerance;
198  fEpsilon = rhs.fEpsilon; fRmin = rhs.fRmin; fRmax = rhs.fRmax;
199  fSPhi = rhs.fSPhi; fDPhi = rhs.fDPhi; fSTheta = rhs.fSTheta;
200  fDTheta = rhs.fDTheta; sinCPhi = rhs.sinCPhi; cosCPhi = rhs.cosCPhi;
201  cosHDPhiOT = rhs.cosHDPhiOT; cosHDPhiIT = rhs.cosHDPhiIT;
202  sinSPhi = rhs.sinSPhi; cosSPhi = rhs.cosSPhi;
203  sinEPhi = rhs.sinEPhi; cosEPhi = rhs.cosEPhi;
204  hDPhi = rhs.hDPhi; cPhi = rhs.cPhi; ePhi = rhs.ePhi;
205  sinSTheta = rhs.sinSTheta; cosSTheta = rhs.cosSTheta;
206  sinETheta = rhs.sinETheta; cosETheta = rhs.cosETheta;
207  tanSTheta = rhs.tanSTheta; tanSTheta2 = rhs.tanSTheta2;
208  tanETheta = rhs.tanETheta; tanETheta2 = rhs.tanETheta2;
209  eTheta = rhs.eTheta; fFullPhiSphere = rhs.fFullPhiSphere;
210  fFullThetaSphere = rhs.fFullThetaSphere; fFullSphere = rhs.fFullSphere;
211  halfCarTolerance = rhs.halfCarTolerance;
212  halfAngTolerance = rhs.halfAngTolerance;
213 
214  return *this;
215 }
G4CSGSolid::operator=
G4CSGSolid & operator=(const G4CSGSolid &rhs)
Definition: G4CSGSolid.cc:91

Here is the call graph for this function:

void G4Sphere::SetDeltaPhiAngle ( G4double  newDphi)
inline

Here is the caller graph for this function:

void G4Sphere::SetDeltaThetaAngle ( G4double  newDTheta)
inline

Here is the caller graph for this function:

void G4Sphere::SetInnerRadius ( G4double  newRMin)
inline
void G4Sphere::SetInsideRadius ( G4double  newRmin)
inline

Here is the caller graph for this function:

void G4Sphere::SetOuterRadius ( G4double  newRmax)
inline

Here is the caller graph for this function:

void G4Sphere::SetStartPhiAngle ( G4double  newSphi,
G4bool  trig = true 
)
inline

Here is the caller graph for this function:

void G4Sphere::SetStartThetaAngle ( G4double  newSTheta)
inline

Here is the caller graph for this function:

std::ostream & G4Sphere::StreamInfo ( std::ostream &  os) const
virtual

Reimplemented from G4CSGSolid.

Definition at line 2773 of file G4Sphere.cc.

2774 {
2775  G4int oldprc = os.precision(16);
2776  os << "-----------------------------------------------------------\n"
2777  << " *** Dump for solid - " << GetName() << " ***\n"
2778  << " ===================================================\n"
2779  << " Solid type: G4Sphere\n"
2780  << " Parameters: \n"
2781  << " inner radius: " << fRmin/mm << " mm \n"
2782  << " outer radius: " << fRmax/mm << " mm \n"
2783  << " starting phi of segment : " << fSPhi/degree << " degrees \n"
2784  << " delta phi of segment : " << fDPhi/degree << " degrees \n"
2785  << " starting theta of segment: " << fSTheta/degree << " degrees \n"
2786  << " delta theta of segment : " << fDTheta/degree << " degrees \n"
2787  << "-----------------------------------------------------------\n";
2788  os.precision(oldprc);
2789 
2790  return os;
2791 }
G4VSolid::GetName
G4String GetName() const
mm
static constexpr double mm
Definition: G4SIunits.hh:115
G4int
int G4int
Definition: G4Types.hh:78
degree
static constexpr double degree
Definition: G4SIunits.hh:144

Here is the call graph for this function:

G4ThreeVector G4Sphere::SurfaceNormal ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 424 of file G4Sphere.cc.

425 {
426  G4int noSurfaces = 0;
427  G4double rho, rho2, radius, pTheta, pPhi=0.;
428  G4double distRMin = kInfinity;
429  G4double distSPhi = kInfinity, distEPhi = kInfinity;
430  G4double distSTheta = kInfinity, distETheta = kInfinity;
431  G4ThreeVector nR, nPs, nPe, nTs, nTe, nZ(0.,0.,1.);
432  G4ThreeVector norm, sumnorm(0.,0.,0.);
433 
434  rho2 = p.x()*p.x()+p.y()*p.y();
435  radius = std::sqrt(rho2+p.z()*p.z());
436  rho = std::sqrt(rho2);
437 
438  G4double distRMax = std::fabs(radius-fRmax);
439  if (fRmin) distRMin = std::fabs(radius-fRmin);
440 
441  if ( rho && !fFullSphere )
442  {
443  pPhi = std::atan2(p.y(),p.x());
444 
445  if (pPhi < fSPhi-halfAngTolerance) { pPhi += twopi; }
446  else if (pPhi > ePhi+halfAngTolerance) { pPhi -= twopi; }
447  }
448  if ( !fFullPhiSphere )
449  {
450  if ( rho )
451  {
452  distSPhi = std::fabs( pPhi-fSPhi );
453  distEPhi = std::fabs( pPhi-ePhi );
454  }
455  else if( !fRmin )
456  {
457  distSPhi = 0.;
458  distEPhi = 0.;
459  }
460  nPs = G4ThreeVector(sinSPhi,-cosSPhi,0);
461  nPe = G4ThreeVector(-sinEPhi,cosEPhi,0);
462  }
463  if ( !fFullThetaSphere )
464  {
465  if ( rho )
466  {
467  pTheta = std::atan2(rho,p.z());
468  distSTheta = std::fabs(pTheta-fSTheta);
469  distETheta = std::fabs(pTheta-eTheta);
470 
471  nTs = G4ThreeVector(-cosSTheta*p.x()/rho,
472  -cosSTheta*p.y()/rho,
473  sinSTheta );
474 
475  nTe = G4ThreeVector( cosETheta*p.x()/rho,
476  cosETheta*p.y()/rho,
477  -sinETheta );
478  }
479  else if( !fRmin )
480  {
481  if ( fSTheta )
482  {
483  distSTheta = 0.;
484  nTs = G4ThreeVector(0.,0.,-1.);
485  }
486  if ( eTheta < pi )
487  {
488  distETheta = 0.;
489  nTe = G4ThreeVector(0.,0.,1.);
490  }
491  }
492  }
493  if( radius ) { nR = G4ThreeVector(p.x()/radius,p.y()/radius,p.z()/radius); }
494 
495  if( distRMax <= halfCarTolerance )
496  {
497  noSurfaces ++;
498  sumnorm += nR;
499  }
500  if( fRmin && (distRMin <= halfCarTolerance) )
501  {
502  noSurfaces ++;
503  sumnorm -= nR;
504  }
505  if( !fFullPhiSphere )
506  {
507  if (distSPhi <= halfAngTolerance)
508  {
509  noSurfaces ++;
510  sumnorm += nPs;
511  }
512  if (distEPhi <= halfAngTolerance)
513  {
514  noSurfaces ++;
515  sumnorm += nPe;
516  }
517  }
518  if ( !fFullThetaSphere )
519  {
520  if ((distSTheta <= halfAngTolerance) && (fSTheta > 0.))
521  {
522  noSurfaces ++;
523  if ((radius <= halfCarTolerance) && fFullPhiSphere) { sumnorm += nZ; }
524  else { sumnorm += nTs; }
525  }
526  if ((distETheta <= halfAngTolerance) && (eTheta < pi))
527  {
528  noSurfaces ++;
529  if ((radius <= halfCarTolerance) && fFullPhiSphere) { sumnorm -= nZ; }
530  else { sumnorm += nTe; }
531  if(sumnorm.z() == 0.) { sumnorm += nZ; }
532  }
533  }
534  if ( noSurfaces == 0 )
535  {
536 #ifdef G4CSGDEBUG
537  G4Exception("G4Sphere::SurfaceNormal(p)", "GeomSolids1002",
538  JustWarning, "Point p is not on surface !?" );
539 #endif
540  norm = ApproxSurfaceNormal(p);
541  }
542  else if ( noSurfaces == 1 ) { norm = sumnorm; }
543  else { norm = sumnorm.unit(); }
544  return norm;
545 }
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
CLHEP::Hep3Vector::x
double x() const
JustWarning
Definition: G4ExceptionSeverity.hh:64
G4int
int G4int
Definition: G4Types.hh:78
CLHEP::Hep3Vector::z
double z() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
CLHEP::Hep3Vector::unit
Hep3Vector unit() const
CLHEP::Hep3Vector::y
double y() const
pi
static constexpr double pi
Definition: G4SIunits.hh:75
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

The documentation for this class was generated from the following files: