G4LegendrePolynomial Class Reference

#include <G4LegendrePolynomial.hh>

Public Member Functions
G4double	GetCoefficient (size_t i, size_t order)
G4double	EvalLegendrePoly (G4int order, G4double x)
G4double	EvalAssocLegendrePoly (G4int l, G4int m, G4double x)

Static Public Member Functions
static size_t	GetNCoefficients (size_t order)

Protected Member Functions
void	BuildUpToOrder (size_t order)

Protected Attributes
std::vector< std::vector < G4double > >	fCoefficients

Detailed Description

Definition at line 49 of file G4LegendrePolynomial.hh.

Member Function Documentation

void G4LegendrePolynomial::BuildUpToOrder ( size_t  order )

protected

Definition at line 102 of file G4LegendrePolynomial.cc.

{
  if(orderMax > 30) {
    G4cout << "G4LegendrePolynomial::GetCoefficient(): "
           << "I refuse to make a Legendre Polynomial of order " 
           << orderMax << G4endl;
    return;
  }
  while(fCoefficients.size() < orderMax+1) {  /* Loop checking, 30-Oct-2015, G.Folger */
    size_t order = fCoefficients.size();
    fCoefficients.resize(order+1);
    if(order <= 1) fCoefficients[order].push_back(1.);
    else {
      for(size_t iCoeff = 0; iCoeff < order+1; ++iCoeff) {
        if((order % 2) == (iCoeff % 2)) {
          G4double coeff = 0;
          if(iCoeff <= order-2) coeff -= fCoefficients[order-2][iCoeff/2]*G4double(order-1);
          if(iCoeff > 0) coeff += fCoefficients[order-1][(iCoeff-1)/2]*G4double(2*order-1);
          coeff /= G4double(order);
          fCoefficients[order].push_back(coeff);
        }
      }
    }
  }
}

G4double G4LegendrePolynomial::EvalAssocLegendrePoly	(	G4int	l,
		G4int	m,
		G4double	x
	)

Definition at line 49 of file G4LegendrePolynomial.cc.

{
  if(l<0 || m<-l || m>l) return 0;
  G4Pow* g4pow =  G4Pow::GetInstance();

  // Use non-log factorial, which is more efficient until l and m get 
  // above 10 or so.
  // FIXME: G4Pow doesn't check whether the argument gets too large, 
  // which is unsafe! Max is 512; VI: It is assume that Geant4 does not
  // need higher order
  if(m<0) return (m%2 ? -1. : 1.) * g4pow->factorial(l+m)/g4pow->factorial(l-m) 
        * EvalAssocLegendrePoly(l, -m, x);

  // hard-code the first few orders for speed
  if(l==0)   return 1;
  if(l==1) {
    if(m==0) return x;
    /*m==1*/ return -sqrt(1.-x*x);
  }
  if(l<5) {
    G4double x2 = x*x;
    if(l==2) {
      if(m==0) return 0.5*(3.*x2 - 1.);
      if(m==1) return -3.*x*sqrt(1.-x2);
      /*m==2*/ return 3.*(1.-x2);
    }
    if(l==3) {
      if(m==0) return 0.5*(5.*x*x2 - 3.*x);
      if(m==1) return -1.5*(5.*x2-1.)*sqrt(1.-x2);
      if(m==2) return 15.*x*(1.-x2);
      /*m==3*/ return -15.*(1.-x2)*sqrt(1.-x2);
    }
    if(l==4) {
      if(m==0) return 0.125*(35.*x2*x2 - 30.*x2 + 3.);
      if(m==1) return -2.5*(7.*x*x2-3.*x)*sqrt(1.-x2);
      if(m==2) return 7.5*(7.*x2-1.)*(1.-x2);
      if(m==3) return -105.*x*(1.-x2)*sqrt(1.-x2);
      /*m==4*/ return 105.*(1. - 2.*x2 + x2*x2);
    }
  }

  // Easy special cases
  // FIXME: G4Pow doesn't check whether the argument gets too large, which is unsafe! Max is 512. 
  if(m==l) return (l%2 ? -1. : 1.) * 
         G4Exp(g4pow->logfactorial(2*l) - g4pow->logfactorial(l)) * 
         G4Exp(G4Log((1.-x*x)*0.25)*0.5*G4double(l));
  if(m==l-1) return x*(2.*G4double(m)+1.)*EvalAssocLegendrePoly(m,m,x);

  // Otherwise calculate recursively
  return (x*G4double(2*l-1)*EvalAssocLegendrePoly(l-1,m,x) - 
      (G4double(l+m-1))*EvalAssocLegendrePoly(l-2,m,x))/G4double(l-m);
}

Here is the call graph for this function:

Here is the caller graph for this function:

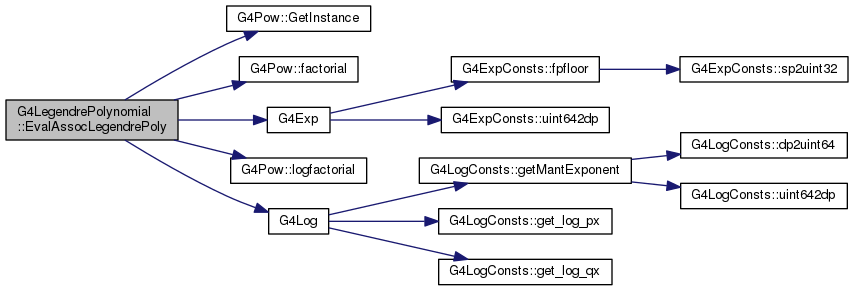
G4double G4LegendrePolynomial::EvalLegendrePoly	(	G4int	order,
		G4double	x
	)

Definition at line 43 of file G4LegendrePolynomial.cc.

{
  // Call EvalAssocLegendrePoly with m=0
  return (EvalAssocLegendrePoly(order,0,x));
}

G4double G4LegendrePolynomial::GetCoefficient	(	size_t	i,
		size_t	order
	)

Definition at line 34 of file G4LegendrePolynomial.cc.

{
  if(order >= fCoefficients.size()) BuildUpToOrder(order);
  if(order >= fCoefficients.size() ||
     i/2 >= fCoefficients[order].size() ||
     (i%2) != order %2) return 0;
  return fCoefficients[order][i/2];
}

Here is the caller graph for this function:

static size_t G4LegendrePolynomial::GetNCoefficients ( size_t  order )

inlinestatic

Definition at line 53 of file G4LegendrePolynomial.hh.

{ return order+1; }

Here is the caller graph for this function:

Member Data Documentation

std::vector< std::vector<G4double> > G4LegendrePolynomial::fCoefficients

protected

Definition at line 62 of file G4LegendrePolynomial.hh.

---

The documentation for this class was generated from the following files:

• source/geant4.10.03.p03/source/processes/hadronic/models/util/include/G4LegendrePolynomial.hh
• source/geant4.10.03.p03/source/processes/hadronic/models/util/src/G4LegendrePolynomial.cc