G4Hype Class Reference

#include <G4Hype.hh>

Inheritance diagram for G4Hype:

Collaboration diagram for G4Hype:

Public Member Functions
	G4Hype (const G4String &pName, G4double newInnerRadius, G4double newOuterRadius, G4double newInnerStereo, G4double newOuterStereo, G4double newHalfLenZ)
virtual	~G4Hype ()
void	ComputeDimensions (G4VPVParameterisation *p, const G4int n, const G4VPhysicalVolume *pRep)
void	Extent (G4ThreeVector &pMin, G4ThreeVector &pMax) const
G4bool	CalculateExtent (const EAxis pAxis, const G4VoxelLimits &pVoxelLimit, const G4AffineTransform &pTransform, G4double &pMin, G4double &pMax) const
G4double	GetInnerRadius () const
G4double	GetOuterRadius () const
G4double	GetZHalfLength () const
G4double	GetInnerStereo () const
G4double	GetOuterStereo () const
void	SetInnerRadius (G4double newIRad)
void	SetOuterRadius (G4double newORad)
void	SetZHalfLength (G4double newHLZ)
void	SetInnerStereo (G4double newISte)
void	SetOuterStereo (G4double newOSte)
EInside	Inside (const G4ThreeVector &p) const
G4ThreeVector	SurfaceNormal (const G4ThreeVector &p) const
G4double	DistanceToIn (const G4ThreeVector &p, const G4ThreeVector &v) const
G4double	DistanceToIn (const G4ThreeVector &p) const
G4double	DistanceToOut (const G4ThreeVector &p, const G4ThreeVector &v, const G4bool calcNorm=G4bool(false), G4bool *validNorm=0, G4ThreeVector *n=0) const
G4double	DistanceToOut (const G4ThreeVector &p) const
G4GeometryType	GetEntityType () const
G4VSolid *	Clone () const
std::ostream &	StreamInfo (std::ostream &os) const
G4double	GetCubicVolume ()
G4double	GetSurfaceArea ()
G4ThreeVector	GetPointOnSurface () const
void	DescribeYourselfTo (G4VGraphicsScene &scene) const
G4VisExtent	GetExtent () const
G4Polyhedron *	CreatePolyhedron () const
G4Polyhedron *	GetPolyhedron () const
	G4Hype (__void__ &)
	G4Hype (const G4Hype &rhs)
G4Hype &	operator= (const G4Hype &rhs)
Public Member Functions inherited from G4VSolid
	G4VSolid (const G4String &name)
virtual	~G4VSolid ()
G4bool	operator== (const G4VSolid &s) const
G4String	GetName () const
void	SetName (const G4String &name)
G4double	GetTolerance () const
void	DumpInfo () const
virtual const G4VSolid *	GetConstituentSolid (G4int no) const
virtual G4VSolid *	GetConstituentSolid (G4int no)
virtual const G4DisplacedSolid *	GetDisplacedSolidPtr () const
virtual G4DisplacedSolid *	GetDisplacedSolidPtr ()
	G4VSolid (__void__ &)
	G4VSolid (const G4VSolid &rhs)
G4VSolid &	operator= (const G4VSolid &rhs)
G4double	EstimateCubicVolume (G4int nStat, G4double epsilon) const
G4double	EstimateSurfaceArea (G4int nStat, G4double ell) const

Protected Types
enum	ESide { outerFace, innerFace, leftCap, rightCap }

Protected Member Functions
G4bool	InnerSurfaceExists () const
G4double	HypeInnerRadius2 (G4double zVal) const
G4double	HypeOuterRadius2 (G4double zVal) const
Protected Member Functions inherited from G4VSolid
void	CalculateClippedPolygonExtent (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
void	ClipCrossSection (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
void	ClipBetweenSections (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
void	ClipPolygon (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis) const

Static Protected Member Functions
static G4double	ApproxDistOutside (G4double pr, G4double pz, G4double r0, G4double tanPhi)
static G4double	ApproxDistInside (G4double pr, G4double pz, G4double r0, G4double tan2Phi)
static G4int	IntersectHype (const G4ThreeVector &p, const G4ThreeVector &v, G4double r2, G4double tan2Phi, G4double s[2])

Protected Attributes
G4double	innerRadius
G4double	outerRadius
G4double	halfLenZ
G4double	innerStereo
G4double	outerStereo
G4double	tanInnerStereo
G4double	tanOuterStereo
G4double	tanInnerStereo2
G4double	tanOuterStereo2
G4double	innerRadius2
G4double	outerRadius2
G4double	endInnerRadius2
G4double	endOuterRadius2
G4double	endInnerRadius
G4double	endOuterRadius
Protected Attributes inherited from G4VSolid
G4double	kCarTolerance

Detailed Description

Definition at line 67 of file G4Hype.hh.

Member Enumeration Documentation

enum G4Hype::ESide

protected

Enumerator
outerFace
innerFace
leftCap
rightCap

Definition at line 183 of file G4Hype.hh.

{outerFace,innerFace,leftCap, rightCap};

Constructor & Destructor Documentation

G4Hype::G4Hype	(	const G4String &	pName,
		G4double	newInnerRadius,
		G4double	newOuterRadius,
		G4double	newInnerStereo,
		G4double	newOuterStereo,
		G4double	newHalfLenZ
	)

Definition at line 74 of file G4Hype.cc.

  : G4VSolid(pName), fCubicVolume(0.), fSurfaceArea(0.),
    fRebuildPolyhedron(false), fpPolyhedron(0)
{
  fHalfTol = 0.5*kCarTolerance;

  // Check z-len
  //
  if (newHalfLenZ<=0)
  {
    std::ostringstream message;
    message << "Invalid Z half-length - " << GetName() << G4endl
            << "        Invalid Z half-length: "
            << newHalfLenZ/mm << " mm";
    G4Exception("G4Hype::G4Hype()", "GeomSolids0002",
                FatalErrorInArgument, message);
  }
  halfLenZ=newHalfLenZ;   

  // Check radii
  //
  if (newInnerRadius<0 || newOuterRadius<0)
  {
    std::ostringstream message;
    message << "Invalid radii - " << GetName() << G4endl
            << "        Invalid radii !  Inner radius: "
            << newInnerRadius/mm << " mm" << G4endl
            << "                         Outer radius: "
            << newOuterRadius/mm << " mm";
    G4Exception("G4Hype::G4Hype()", "GeomSolids0002",
                FatalErrorInArgument, message);
  }
  if (newInnerRadius >= newOuterRadius)
  {
    std::ostringstream message;
    message << "Outer > inner radius - " << GetName() << G4endl
            << "        Invalid radii !  Inner radius: "
            << newInnerRadius/mm << " mm" << G4endl
            << "                         Outer radius: "
            << newOuterRadius/mm << " mm";
    G4Exception("G4Hype::G4Hype()", "GeomSolids0002",
                FatalErrorInArgument, message);
  }

  innerRadius=newInnerRadius;
  outerRadius=newOuterRadius;

  innerRadius2=innerRadius*innerRadius;
  outerRadius2=outerRadius*outerRadius;
    
  SetInnerStereo( newInnerStereo );
  SetOuterStereo( newOuterStereo );
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4Hype::~G4Hype ( )

virtual

Definition at line 152 of file G4Hype.cc.

{
  delete fpPolyhedron; fpPolyhedron = 0;
}

G4Hype::G4Hype

(

__void__ &

a

)

Definition at line 138 of file G4Hype.cc.

  : G4VSolid(a), innerRadius(0.), outerRadius(0.), halfLenZ(0.), innerStereo(0.),
    outerStereo(0.), tanInnerStereo(0.), tanOuterStereo(0.), tanInnerStereo2(0.),
    tanOuterStereo2(0.), innerRadius2(0.), outerRadius2(0.), endInnerRadius2(0.),
    endOuterRadius2(0.), endInnerRadius(0.), endOuterRadius(0.),
    fCubicVolume(0.), fSurfaceArea(0.), fHalfTol(0.),
    fRebuildPolyhedron(false), fpPolyhedron(0)
{
}

G4Hype::G4Hype

(

const G4Hype &

rhs

)

Definition at line 161 of file G4Hype.cc.

  : G4VSolid(rhs), innerRadius(rhs.innerRadius),
    outerRadius(rhs.outerRadius), halfLenZ(rhs.halfLenZ),
    innerStereo(rhs.innerStereo), outerStereo(rhs.outerStereo),
    tanInnerStereo(rhs.tanInnerStereo), tanOuterStereo(rhs.tanOuterStereo),
    tanInnerStereo2(rhs.tanInnerStereo2), tanOuterStereo2(rhs.tanOuterStereo2),
    innerRadius2(rhs.innerRadius2), outerRadius2(rhs.outerRadius2),
    endInnerRadius2(rhs.endInnerRadius2), endOuterRadius2(rhs.endOuterRadius2),
    endInnerRadius(rhs.endInnerRadius), endOuterRadius(rhs.endOuterRadius),
    fCubicVolume(rhs.fCubicVolume), fSurfaceArea(rhs.fSurfaceArea),
    fHalfTol(rhs.fHalfTol), fRebuildPolyhedron(false), fpPolyhedron(0)
{
}

Member Function Documentation

G4double G4Hype::ApproxDistInside ( G4double  pr, G4double  pz, G4double  r0, G4double  tan2Phi  )

staticprotected

Definition at line 1091 of file G4Hype.cc.

{
  if (tan2Phi < DBL_MIN) return r0 - pr;

  //
  // Corresponding position and normal on hyperbolic
  //
  G4double rh = std::sqrt( r0*r0 + pz*pz*tan2Phi );
  
  G4double dr = -rh;
  G4double dz = pz*tan2Phi;
  G4double len = std::sqrt(dr*dr + dz*dz);
  
  //
  // Answer
  //
  return std::fabs((pr-rh)*dr)/len;
}

Here is the caller graph for this function:

G4double G4Hype::ApproxDistOutside ( G4double  pr, G4double  pz, G4double  r0, G4double  tanPhi  )

staticprotected

Definition at line 1033 of file G4Hype.cc.

{
  if (tanPhi < DBL_MIN) return pr-r0;

  G4double tan2Phi = tanPhi*tanPhi;

  //
  // First point
  //
  G4double z1 = pz;
  G4double r1 = std::sqrt( r0*r0 + z1*z1*tan2Phi );
  
  //
  // Second point
  //
  G4double z2 = (pr*tanPhi + pz)/(1 + tan2Phi);
  G4double r2 = std::sqrt( r0*r0 + z2*z2*tan2Phi );
  
  //
  // Line between them
  //
  G4double dr = r2-r1;
  G4double dz = z2-z1;
  
  G4double len = std::sqrt(dr*dr + dz*dz);
  if (len < DBL_MIN)
  {
    //
    // The two points are the same?? I guess we
    // must have really bracketed the normal
    //
    dr = pr-r1;
    dz = pz-z1;
    return std::sqrt( dr*dr + dz*dz );
  }
  
  //
  // Distance
  //
  return std::fabs((pr-r1)*dz - (pz-z1)*dr)/len;
}

Here is the caller graph for this function:

G4bool G4Hype::CalculateExtent ( const EAxis  pAxis, const G4VoxelLimits &  pVoxelLimit, const G4AffineTransform &  pTransform, G4double &  pMin, G4double &  pMax  ) const

virtual

Implements G4VSolid.

Definition at line 246 of file G4Hype.cc.

{
  G4ThreeVector bmin, bmax;

  // Get bounding box
  Extent(bmin,bmax);

  // Find extent
  G4BoundingEnvelope bbox(bmin,bmax);
  return bbox.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
}

Here is the call graph for this function:

G4VSolid * G4Hype::Clone ( ) const

virtual

Reimplemented from G4VSolid.

Definition at line 1124 of file G4Hype.cc.

{
  return new G4Hype(*this);
}

Here is the call graph for this function:

void G4Hype::ComputeDimensions ( G4VPVParameterisation *  p, const G4int  n, const G4VPhysicalVolume *  pRep  )

virtual

Reimplemented from G4VSolid.

Definition at line 212 of file G4Hype.cc.

{
  p->ComputeDimensions(*this,n,pRep);
}

Here is the call graph for this function:

G4Polyhedron * G4Hype::CreatePolyhedron ( ) const

virtual

Reimplemented from G4VSolid.

Definition at line 1306 of file G4Hype.cc.

{
   return new G4PolyhedronHype(innerRadius, outerRadius,
                               tanInnerStereo2, tanOuterStereo2, halfLenZ);
}

Here is the caller graph for this function:

void G4Hype::DescribeYourselfTo ( G4VGraphicsScene &  scene ) const

virtual

Implements G4VSolid.

Definition at line 1284 of file G4Hype.cc.

{
  scene.AddSolid (*this);
}

Here is the call graph for this function:

G4double G4Hype::DistanceToIn ( const G4ThreeVector &  p, const G4ThreeVector &  v  ) const

virtual

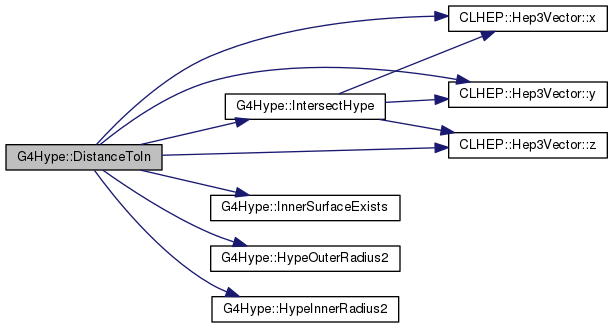
Implements G4VSolid.

Definition at line 355 of file G4Hype.cc.

{
  //
  // Quick test. Beware! This assumes v is a unit vector!
  //
  if (std::fabs(p.x()*v.y() - p.y()*v.x()) > endOuterRadius+kCarTolerance)
    return kInfinity;
  
  //
  // Take advantage of z symmetry, and reflect throught the
  // z=0 plane so that pz is always positive
  //
  G4double pz(p.z()), vz(v.z());
  if (pz < 0)
  {
    pz = -pz;
    vz = -vz;
  }

  //
  // We must be very careful if we don't want to
  // create subtle leaks at the edges where the
  // hyperbolic surfaces connect to the endplate.
  // The only reliable way to do so is to make sure
  // that the decision as to when a track passes
  // over the edge of one surface is exactly the
  // same decision as to when a track passes into the
  // other surface. By "exact", we don't mean algebraicly
  // exact, but we mean the same machine instructions
  // should be used.
  //
  G4bool couldMissOuter(true),
         couldMissInner(true),
         cantMissInnerCylinder(false);
  
  //
  // Check endplate intersection
  //
  G4double sigz = pz-halfLenZ;
  
  if (sigz > -fHalfTol)    // equivalent to: if (pz > halfLenZ - fHalfTol)
  {
    //
    // We start in front of the endplate (within roundoff)
    // Correct direction to intersect endplate?
    //
    if (vz >= 0)
    {
      //
      // Nope. As long as we are far enough away, we
      // can't intersect anything
      //
      if (sigz > 0) return kInfinity;
      
      //
      // Otherwise, we may still hit a hyperbolic surface
      // if the point is on the hyperbolic surface (within tolerance)
      //
      G4double pr2 = p.x()*p.x() + p.y()*p.y();
      if (pr2 > endOuterRadius2 + kCarTolerance*endOuterRadius)
        return kInfinity;
      
      if (InnerSurfaceExists())
      {
        if (pr2 < endInnerRadius2 - kCarTolerance*endInnerRadius)
          return kInfinity;
        if ( (pr2 < endOuterRadius2 - kCarTolerance*endOuterRadius)
          && (pr2 > endInnerRadius2 + kCarTolerance*endInnerRadius) )
          return kInfinity;
      }
      else
      {
        if (pr2 < endOuterRadius2 - kCarTolerance*endOuterRadius)
          return kInfinity;
      }
    }
    else
    {
      //
      // Where do we intersect at z = halfLenZ?
      //
      G4double q = -sigz/vz;
      G4double xi = p.x() + q*v.x(),
               yi = p.y() + q*v.y();
         
      //
      // Is this on the endplate? If so, return s, unless
      // we are on the tolerant surface, in which case return 0
      //
      G4double pr2 = xi*xi + yi*yi;
      if (pr2 <= endOuterRadius2)
      {
        if (InnerSurfaceExists())
        {
          if (pr2 >= endInnerRadius2) return (sigz < fHalfTol) ? 0 : q;
          //
          // This test is sufficient to ensure that the
          // trajectory cannot miss the inner hyperbolic surface
          // for z > 0, if the normal is correct.
          //
          G4double dot1 = (xi*v.x() + yi*v.y())*endInnerRadius/std::sqrt(pr2);
          couldMissInner = (dot1 - halfLenZ*tanInnerStereo2*vz <= 0);
          
          if (pr2 > endInnerRadius2*(1 - 2*DBL_EPSILON) )
          {
            //
            // There is a potential leak if the inner
            // surface is a cylinder
            //
            if ( (innerStereo < DBL_MIN)
              && ((std::fabs(v.x()) > DBL_MIN) || (std::fabs(v.y()) > DBL_MIN)))
              cantMissInnerCylinder = true;
          }
        }
        else
        {
          return (sigz < fHalfTol) ? 0 : q;
        }
      }
      else
      {
        G4double dotR( xi*v.x() + yi*v.y() );
        if (dotR >= 0)
        {
          //
          // Otherwise, if we are traveling outwards, we know
          // we must miss the hyperbolic surfaces also, so
          // we need not bother checking
          //
          return kInfinity;
        }
        else
        {
          //
          // This test is sufficient to ensure that the
          // trajectory cannot miss the outer hyperbolic surface
          // for z > 0, if the normal is correct.
          //
          G4double dot1 = dotR*endOuterRadius/std::sqrt(pr2);
          couldMissOuter = (dot1 - halfLenZ*tanOuterStereo2*vz>= 0);
        }
      }
    }
  }
    
  //
  // Check intersection with outer hyperbolic surface, save
  // distance to valid intersection into "best".
  //    
  G4double best = kInfinity;
  
  G4double q[2];
  G4int n = IntersectHype( p, v, outerRadius2, tanOuterStereo2, q );
  
  if (n > 0)
  {
    //
    // Potential intersection: is p on this surface?
    //
    if (pz < halfLenZ+fHalfTol)
    {
      G4double dr2 = p.x()*p.x() + p.y()*p.y() - HypeOuterRadius2(pz);
      if (std::fabs(dr2) < kCarTolerance*endOuterRadius)
      {
        //
        // Sure, but make sure we're traveling inwards at
        // this point
        //
        if (p.x()*v.x() + p.y()*v.y() - pz*tanOuterStereo2*vz < 0)
          return 0;
      }
    }
    
    //
    // We are now certain that p is not on the tolerant surface.
    // Accept only position distance q
    //
    G4int i;
    for( i=0; i<n; i++ )
    {
      if (q[i] >= 0)
      {
        //
        // Check to make sure this intersection point is
        // on the surface, but only do so if we haven't
        // checked the endplate intersection already
        //
        G4double zi = pz + q[i]*vz;
        
        if (zi < -halfLenZ) continue;
        if (zi > +halfLenZ && couldMissOuter) continue;
        
        //
        // Check normal
        //
        G4double xi = p.x() + q[i]*v.x(),
           yi = p.y() + q[i]*v.y();
           
        if (xi*v.x() + yi*v.y() - zi*tanOuterStereo2*vz > 0) continue;

        best = q[i];
        break;
      }
    }
  }
  
  if (!InnerSurfaceExists()) return best;    
  
  //
  // Check intersection with inner hyperbolic surface
  //
  n = IntersectHype( p, v, innerRadius2, tanInnerStereo2, q );  
  if (n == 0)
  {
    if (cantMissInnerCylinder) return (sigz < fHalfTol) ? 0 : -sigz/vz;
        
    return best;
  }
  
  //
  // P on this surface?
  //
  if (pz < halfLenZ+fHalfTol)
  {
    G4double dr2 = p.x()*p.x() + p.y()*p.y() - HypeInnerRadius2(pz);
    if (std::fabs(dr2) < kCarTolerance*endInnerRadius)
    {
      //
      // Sure, but make sure we're traveling outwards at
      // this point
      //
      if (p.x()*v.x() + p.y()*v.y() - pz*tanInnerStereo2*vz > 0) return 0;
    }
  }
  
  //
  // No, so only positive q is valid. Search for a valid intersection
  // that is closer than the outer intersection (if it exists)
  //
  G4int i;
  for( i=0; i<n; i++ )
  {
    if (q[i] > best) break;
    if (q[i] >= 0)
    {
      //
      // Check to make sure this intersection point is
      // on the surface, but only do so if we haven't
      // checked the endplate intersection already
      //
      G4double zi = pz + q[i]*vz;

      if (zi < -halfLenZ) continue;
      if (zi > +halfLenZ && couldMissInner) continue;

      //
      // Check normal
      //
      G4double xi = p.x() + q[i]*v.x(),
         yi = p.y() + q[i]*v.y();

      if (xi*v.x() + yi*v.y() - zi*tanOuterStereo2*vz < 0) continue;

      best = q[i];
      break;
    }
  }
    
  //
  // Done
  //
  return best;
}

Here is the call graph for this function:

G4double G4Hype::DistanceToIn ( const G4ThreeVector &  p ) const

virtual

Implements G4VSolid.

Definition at line 650 of file G4Hype.cc.

{
  G4double absZ(std::fabs(p.z()));
  
  //
  // Check region
  //
  G4double r2 = p.x()*p.x() + p.y()*p.y();
  G4double r = std::sqrt(r2);
  
  G4double sigz = absZ - halfLenZ;
  
  if (r < endOuterRadius)
  {
    if (sigz > -fHalfTol)
    {
      if (InnerSurfaceExists())
      {
        if (r > endInnerRadius) 
          return sigz < fHalfTol ? 0 : sigz;  // Region 1
        
        G4double dr = endInnerRadius - r;
        if (sigz > dr*tanInnerStereo2)
        {
          //
          // In region 5
          //
          G4double answer = std::sqrt( dr*dr + sigz*sigz );
          return answer < fHalfTol ? 0 : answer;
        }
      }
      else
      {
        //
        // In region 1 (no inner surface)
        //
        return sigz < fHalfTol ? 0 : sigz;
      }
    }
  }
  else
  {
    G4double dr = r - endOuterRadius;
    if (sigz > -dr*tanOuterStereo2)
    {
      //
      // In region 2
      //
      G4double answer = std::sqrt( dr*dr + sigz*sigz );
      return answer < fHalfTol ? 0 : answer;
    }
  }
  
  if (InnerSurfaceExists())
  {
    if (r2 < HypeInnerRadius2(absZ)+kCarTolerance*endInnerRadius)
    {
       //
      // In region 4
      //
      G4double answer = ApproxDistInside( r,absZ,innerRadius,tanInnerStereo2 );
      return answer < fHalfTol ? 0 : answer;
    }
  }
  
  //
  // We are left by elimination with region 3
  //
  G4double answer = ApproxDistOutside( r, absZ, outerRadius, tanOuterStereo );
  return answer < fHalfTol ? 0 : answer;
}

Here is the call graph for this function:

G4double G4Hype::DistanceToOut ( const G4ThreeVector &  p, const G4ThreeVector &  v, const G4bool  calcNorm = G4bool(false), G4bool *  validNorm = 0, G4ThreeVector *  n = 0  ) const

virtual

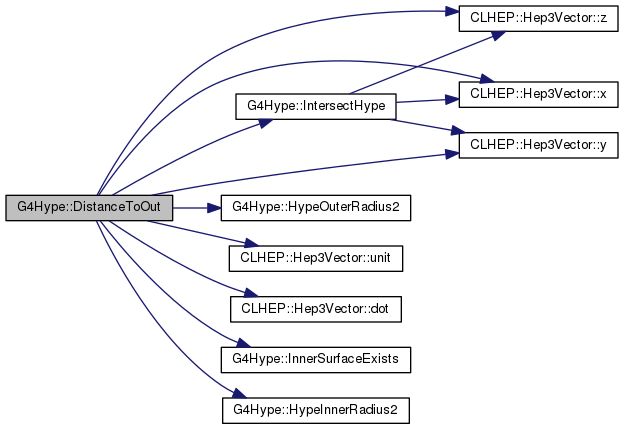
Implements G4VSolid.

Definition at line 731 of file G4Hype.cc.

{
  static const G4ThreeVector normEnd1(0.0,0.0,+1.0);
  static const G4ThreeVector normEnd2(0.0,0.0,-1.0);
  
  //
  // Keep track of closest surface
  //
  G4double sBest;        // distance to
  const G4ThreeVector *nBest;    // normal vector
  G4bool vBest;        // whether "valid"

  //
  // Check endplate, taking advantage of symmetry.
  // Note that the endcap is the only surface which
  // has a "valid" normal, i.e. is a surface of which
  // the entire solid is behind.
  //
  G4double pz(p.z()), vz(v.z());
  if (vz < 0)
  {
    pz = -pz;
    vz = -vz;
    nBest = &normEnd2;
  }
  else
    nBest = &normEnd1;

  //
  // Possible intercept. Are we on the surface?
  //
  if (pz > halfLenZ-fHalfTol)
  {
    if (calcNorm) { *norm = *nBest; *validNorm = true; }
    return 0;
  }

  //
  // Nope. Get distance. Beware of zero vz.
  //
  sBest = (vz > DBL_MIN) ? (halfLenZ - pz)/vz : kInfinity;
  vBest = true;
  
  //
  // Check outer surface
  //
  G4double r2 = p.x()*p.x() + p.y()*p.y();
  
  G4double q[2];
  G4int n = IntersectHype( p, v, outerRadius2, tanOuterStereo2, q );
  
  G4ThreeVector norm1, norm2;

  if (n > 0)
  {
    //
    // We hit somewhere. Are we on the surface?
    //  
    G4double dr2 = r2 - HypeOuterRadius2(pz);
    if (std::fabs(dr2) < endOuterRadius*kCarTolerance)
    {
      G4ThreeVector normHere( p.x(), p.y(), -p.z()*tanOuterStereo2 );
      //
      // Sure. But are we going the right way?
      //
      if (normHere.dot(v) > 0)
      {
        if (calcNorm) { *norm = normHere.unit(); *validNorm = false; }
        return 0;
      }
    }
    
    //
    // Nope. Check closest positive intercept.
    //
    G4int i;
    for( i=0; i<n; i++ )
    {
      if (q[i] > sBest) break;
      if (q[i] > 0)
      {
        //
        // Make sure normal is correct (that this
        // solution is an outgoing solution)
        //
        G4ThreeVector pk(p+q[i]*v);
        norm1 = G4ThreeVector( pk.x(), pk.y(), -pk.z()*tanOuterStereo2 );
        if (norm1.dot(v) > 0)
        {
          sBest = q[i];
          nBest = &norm1;
          vBest = false;
          break;
        }
      }
    }
  }
  
  if (InnerSurfaceExists())
  {
    //
    // Check inner surface
    //
    n = IntersectHype( p, v, innerRadius2, tanInnerStereo2, q );
    if (n > 0)
    {
      //
      // On surface?
      //
      G4double dr2 = r2 - HypeInnerRadius2(pz);
      if (std::fabs(dr2) < endInnerRadius*kCarTolerance)
      {
        G4ThreeVector normHere( -p.x(), -p.y(), p.z()*tanInnerStereo2 );
        if (normHere.dot(v) > 0)
        {
          if (calcNorm)
          {
            *norm = normHere.unit();
            *validNorm = false;
          }
          return 0;
        }
      }
      
      //
      // Check closest positive
      //
      G4int i;
      for( i=0; i<n; i++ )
      {
        if (q[i] > sBest) break;
        if (q[i] > 0)
        {
          G4ThreeVector pk(p+q[i]*v);
          norm2 = G4ThreeVector( -pk.x(), -pk.y(), pk.z()*tanInnerStereo2 );
          if (norm2.dot(v) > 0)
          {
            sBest = q[i];
            nBest = &norm2;
            vBest = false;
            break;
          }
        }
      }
    }
  }
  
  //
  // Done!
  //
  if (calcNorm)
  {
    *validNorm = vBest;
    
    if (nBest == &norm1 || nBest == &norm2) 
      *norm = nBest->unit();
    else
      *norm = *nBest;
  }
  
  return sBest;
}

Here is the call graph for this function:

G4double G4Hype::DistanceToOut ( const G4ThreeVector &  p ) const

virtual

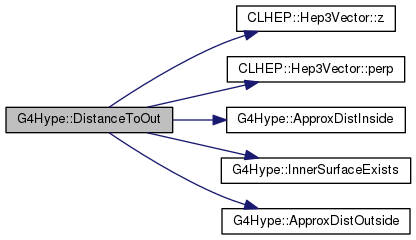
Implements G4VSolid.

Definition at line 902 of file G4Hype.cc.

{
  //
  // Try each surface and remember the closest
  //
  G4double absZ(std::fabs(p.z()));
  G4double r(p.perp());
  
  G4double sBest = halfLenZ - absZ;
  
  G4double tryOuter = ApproxDistInside( r, absZ, outerRadius, tanOuterStereo2 );
  if (tryOuter < sBest)
    sBest = tryOuter;
  
  if (InnerSurfaceExists())
  {
    G4double tryInner = ApproxDistOutside( r,absZ,innerRadius,tanInnerStereo );
    if (tryInner < sBest) sBest = tryInner;
  }
  
  return sBest < 0.5*kCarTolerance ? 0 : sBest;
}

Here is the call graph for this function:

void G4Hype::Extent ( G4ThreeVector &  pMin, G4ThreeVector &  pMax  ) const

virtual

Reimplemented from G4VSolid.

Definition at line 223 of file G4Hype.cc.

{
  pMin.set(-endOuterRadius,-endOuterRadius,-halfLenZ);
  pMax.set( endOuterRadius, endOuterRadius, halfLenZ);

  // Check correctness of the bounding box
  //
  if (pMin.x() >= pMax.x() || pMin.y() >= pMax.y() || pMin.z() >= pMax.z())
  {
    std::ostringstream message;
    message << "Bad bounding box (min >= max) for solid: "
            << GetName() << " !"
            << "\npMin = " << pMin
            << "\npMax = " << pMax;
    G4Exception("G4Hype::Extent()", "GeomMgt0001", JustWarning, message);
    DumpInfo();
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Hype::GetCubicVolume ( )

virtual

Reimplemented from G4VSolid.

Definition at line 1133 of file G4Hype.cc.

{
  if(fCubicVolume != 0.) {;}
    else { fCubicVolume = G4VSolid::GetCubicVolume(); }
  return fCubicVolume;
}

Here is the call graph for this function:

G4GeometryType G4Hype::GetEntityType ( ) const

virtual

Implements G4VSolid.

Definition at line 1115 of file G4Hype.cc.

{
  return G4String("G4Hype");
}

G4VisExtent G4Hype::GetExtent ( ) const

virtual

Reimplemented from G4VSolid.

Definition at line 1293 of file G4Hype.cc.

{
  // Define the sides of the box into which the G4Tubs instance would fit.
  //
  return G4VisExtent( -endOuterRadius, endOuterRadius, 
                      -endOuterRadius, endOuterRadius, 
                      -halfLenZ, halfLenZ );
}

G4double G4Hype::GetInnerRadius ( ) const

inline

Here is the caller graph for this function:

G4double G4Hype::GetInnerStereo ( ) const

inline

Here is the caller graph for this function:

G4double G4Hype::GetOuterRadius ( ) const

inline

Here is the caller graph for this function:

G4double G4Hype::GetOuterStereo ( ) const

inline

Here is the caller graph for this function:

G4ThreeVector G4Hype::GetPointOnSurface ( ) const

virtual

Reimplemented from G4VSolid.

Definition at line 1179 of file G4Hype.cc.

{
  G4double xRand, yRand, zRand, r2 , aOne, aTwo, aThree, chose, sinhu;
  G4double phi, cosphi, sinphi, rBar2Out, rBar2In, alpha, t, rOut, rIn2, rOut2;

  // we use the formula of the area of a surface of revolution to compute 
  // the areas, using the equation of the hyperbola:
  // x^2 + y^2 = (z*tanphi)^2 + r^2

  rBar2Out = outerRadius2;
  alpha = 2.*pi*rBar2Out*std::cos(outerStereo)/tanOuterStereo;
  t     = halfLenZ*tanOuterStereo/(outerRadius*std::cos(outerStereo));
  t     = std::log(t+std::sqrt(sqr(t)+1));
  aOne  = std::fabs(2.*alpha*(std::sinh(2.*t)/4.+t/2.));


  rBar2In = innerRadius2;
  alpha = 2.*pi*rBar2In*std::cos(innerStereo)/tanInnerStereo;
  t     = halfLenZ*tanInnerStereo/(innerRadius*std::cos(innerStereo));
  t     = std::log(t+std::sqrt(sqr(t)+1));
  aTwo  = std::fabs(2.*alpha*(std::sinh(2.*t)/4.+t/2.));

  aThree = pi*((outerRadius2+sqr(halfLenZ*tanOuterStereo)
              -(innerRadius2+sqr(halfLenZ*tanInnerStereo))));
  
  if(outerStereo == 0.) {aOne = std::fabs(2.*pi*outerRadius*2.*halfLenZ);}
  if(innerStereo == 0.) {aTwo = std::fabs(2.*pi*innerRadius*2.*halfLenZ);}
  
  phi = G4RandFlat::shoot(0.,2.*pi);
  cosphi = std::cos(phi);
  sinphi = std::sin(phi);
  sinhu = G4RandFlat::shoot(-1.*halfLenZ*tanOuterStereo/outerRadius,
                          halfLenZ*tanOuterStereo/outerRadius);

  chose = G4RandFlat::shoot(0.,aOne+aTwo+2.*aThree);
  if(chose>=0. && chose < aOne)
  {
    if(outerStereo != 0.)
    {
      zRand = outerRadius*sinhu/tanOuterStereo;
      xRand = std::sqrt(sqr(sinhu)+1)*outerRadius*cosphi;
      yRand = std::sqrt(sqr(sinhu)+1)*outerRadius*sinphi;
      return G4ThreeVector (xRand, yRand, zRand);
    }
    else
    {
      return G4ThreeVector(outerRadius*cosphi,outerRadius*sinphi,
                           G4RandFlat::shoot(-halfLenZ,halfLenZ));
    }
  }
  else if(chose>=aOne && chose<aOne+aTwo)
  {
    if(innerStereo != 0.)
    {
      sinhu = G4RandFlat::shoot(-1.*halfLenZ*tanInnerStereo/innerRadius,
                                halfLenZ*tanInnerStereo/innerRadius);
      zRand = innerRadius*sinhu/tanInnerStereo;
      xRand = std::sqrt(sqr(sinhu)+1)*innerRadius*cosphi;
      yRand = std::sqrt(sqr(sinhu)+1)*innerRadius*sinphi;
      return G4ThreeVector (xRand, yRand, zRand);
    }
    else 
    {
      return G4ThreeVector(innerRadius*cosphi,innerRadius*sinphi,
                           G4RandFlat::shoot(-1.*halfLenZ,halfLenZ));
    }
  }
  else if(chose>=aOne+aTwo && chose<aOne+aTwo+aThree)
  {
    rIn2  = innerRadius2+tanInnerStereo2*halfLenZ*halfLenZ;
    rOut2 = outerRadius2+tanOuterStereo2*halfLenZ*halfLenZ;
    rOut  = std::sqrt(rOut2) ;
 
    do    // Loop checking, 13.08.2015, G.Cosmo
    {
      xRand = G4RandFlat::shoot(-rOut,rOut) ;
      yRand = G4RandFlat::shoot(-rOut,rOut) ;
      r2 = xRand*xRand + yRand*yRand ;
    } while ( ! ( r2 >= rIn2 && r2 <= rOut2 ) ) ;

    zRand = halfLenZ;
    return G4ThreeVector (xRand, yRand, zRand);
  }
  else
  {
    rIn2  = innerRadius2+tanInnerStereo2*halfLenZ*halfLenZ;
    rOut2 = outerRadius2+tanOuterStereo2*halfLenZ*halfLenZ;
    rOut  = std::sqrt(rOut2) ;
 
    do    // Loop checking, 13.08.2015, G.Cosmo
    {
      xRand = G4RandFlat::shoot(-rOut,rOut) ;
      yRand = G4RandFlat::shoot(-rOut,rOut) ;
      r2 = xRand*xRand + yRand*yRand ;
    } while ( ! ( r2 >= rIn2 && r2 <= rOut2 ) ) ;

    zRand = -1.*halfLenZ;
    return G4ThreeVector (xRand, yRand, zRand);
  }
}

Here is the call graph for this function:

G4Polyhedron * G4Hype::GetPolyhedron ( ) const

virtual

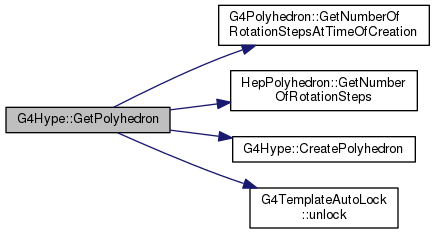
Reimplemented from G4VSolid.

Definition at line 1316 of file G4Hype.cc.

{
  if (!fpPolyhedron ||
      fRebuildPolyhedron ||
      fpPolyhedron->GetNumberOfRotationStepsAtTimeOfCreation() !=
      fpPolyhedron->GetNumberOfRotationSteps())
    {
      G4AutoLock l(&polyhedronMutex);
      delete fpPolyhedron;
      fpPolyhedron = CreatePolyhedron();
      fRebuildPolyhedron = false;
      l.unlock();
    }
  return fpPolyhedron;
}

Here is the call graph for this function:

G4double G4Hype::GetSurfaceArea ( )

virtual

Reimplemented from G4VSolid.

Definition at line 1144 of file G4Hype.cc.

{
  if(fSurfaceArea != 0.) {;}
  else   { fSurfaceArea = G4VSolid::GetSurfaceArea(); }
  return fSurfaceArea;
}

Here is the call graph for this function:

G4double G4Hype::GetZHalfLength ( ) const

inline

Here is the caller graph for this function:

G4double G4Hype::HypeInnerRadius2 ( G4double  zVal ) const

inlineprotected

Here is the caller graph for this function:

G4double G4Hype::HypeOuterRadius2 ( G4double  zVal ) const

inlineprotected

Here is the caller graph for this function:

G4bool G4Hype::InnerSurfaceExists ( ) const

inlineprotected

Here is the caller graph for this function:

EInside G4Hype::Inside ( const G4ThreeVector &  p ) const

virtual

Implements G4VSolid.

Definition at line 265 of file G4Hype.cc.

{
  //
  // Check z extents: are we outside?
  //
  const G4double absZ(std::fabs(p.z()));
  if (absZ > halfLenZ + fHalfTol) return kOutside;
  
  //
  // Check outer radius
  //
  const G4double oRad2(HypeOuterRadius2(absZ));
  const G4double xR2( p.x()*p.x()+p.y()*p.y() );
  
  if (xR2 > oRad2 + kCarTolerance*endOuterRadius) return kOutside;
  
  if (xR2 > oRad2 - kCarTolerance*endOuterRadius) return kSurface;
  
  if (InnerSurfaceExists())
  {
    //
    // Check inner radius
    //
    const G4double iRad2(HypeInnerRadius2(absZ));
    
    if (xR2 < iRad2 - kCarTolerance*endInnerRadius) return kOutside;
    
    if (xR2 < iRad2 + kCarTolerance*endInnerRadius) return kSurface;
  }
  
  //
  // We are inside in radius, now check endplate surface
  //
  if (absZ > halfLenZ - fHalfTol) return kSurface;
  
  return kInside;
}

Here is the call graph for this function:

G4int G4Hype::IntersectHype ( const G4ThreeVector &  p, const G4ThreeVector &  v, G4double  r2, G4double  tan2Phi, G4double  s[2]  )

staticprotected

Definition at line 965 of file G4Hype.cc.

{
  G4double x0 = p.x(), y0 = p.y(), z0 = p.z();
  G4double tx = v.x(), ty = v.y(), tz = v.z();

  G4double a = tx*tx + ty*ty - tz*tz*tan2Phi;
  G4double b = 2*( x0*tx + y0*ty - z0*tz*tan2Phi );
  G4double c = x0*x0 + y0*y0 - r2 - z0*z0*tan2Phi;
  
  if (std::fabs(a) < DBL_MIN)
  {
    //
    // The trajectory is parallel to the asympotic limit of
    // the surface: single solution
    //
    if (std::fabs(b) < DBL_MIN) return 0;
    // Unless we travel through exact center
    
    ss[0] = c/b;
    return 1;
  }
    
  
  G4double radical = b*b - 4*a*c;
  
  if (radical < -DBL_MIN) return 0;    // No solution
  
  if (radical < DBL_MIN)
  {
    //
    // Grazes surface
    //
    ss[0] = -b/a/2.0;
    return 1;
  }
  
  radical = std::sqrt(radical);
  
  G4double q = -0.5*( b + (b < 0 ? -radical : +radical) );
  G4double sa = q/a;
  G4double sb = c/q;    
  if (sa < sb) { ss[0] = sa; ss[1] = sb; } else { ss[0] = sb; ss[1] = sa; }
  return 2;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4Hype & G4Hype::operator=

(

const G4Hype &

rhs

)

Definition at line 179 of file G4Hype.cc.

{
   // Check assignment to self
   //
   if (this == &rhs)  { return *this; }

   // Copy base class data
   //
   G4VSolid::operator=(rhs);

   // Copy data
   //
   innerRadius = rhs.innerRadius; outerRadius = rhs.outerRadius;
   halfLenZ = rhs.halfLenZ;
   innerStereo = rhs.innerStereo; outerStereo = rhs.outerStereo;
   tanInnerStereo = rhs.tanInnerStereo; tanOuterStereo = rhs.tanOuterStereo;
   tanInnerStereo2 = rhs.tanInnerStereo2; tanOuterStereo2 = rhs.tanOuterStereo2;
   innerRadius2 = rhs.innerRadius2; outerRadius2 = rhs.outerRadius2;
   endInnerRadius2 = rhs.endInnerRadius2; endOuterRadius2 = rhs.endOuterRadius2;
   endInnerRadius = rhs.endInnerRadius; endOuterRadius = rhs.endOuterRadius;
   fCubicVolume = rhs.fCubicVolume; fSurfaceArea = rhs.fSurfaceArea;
   fHalfTol = rhs.fHalfTol;
   fRebuildPolyhedron = false;
   delete fpPolyhedron; fpPolyhedron = 0;

   return *this;
}

Here is the call graph for this function:

void G4Hype::SetInnerRadius ( G4double  newIRad )

inline

Here is the caller graph for this function:

void G4Hype::SetInnerStereo ( G4double  newISte )

inline

Here is the caller graph for this function:

void G4Hype::SetOuterRadius ( G4double  newORad )

inline

Here is the caller graph for this function:

void G4Hype::SetOuterStereo ( G4double  newOSte )

inline

Here is the caller graph for this function:

void G4Hype::SetZHalfLength ( G4double  newHLZ )

inline

Here is the caller graph for this function:

std::ostream & G4Hype::StreamInfo ( std::ostream &  os ) const

virtual

Implements G4VSolid.

Definition at line 1155 of file G4Hype.cc.

{
  G4int oldprc = os.precision(16);
  os << "-----------------------------------------------------------\n"
     << "    *** Dump for solid - " << GetName() << " ***\n"
     << "    ===================================================\n"
     << " Solid type: G4Hype\n"
     << " Parameters: \n"
     << "    half length Z: " << halfLenZ/mm << " mm \n"
     << "    inner radius : " << innerRadius/mm << " mm \n"
     << "    outer radius : " << outerRadius/mm << " mm \n"
     << "    inner stereo angle : " << innerStereo/degree << " degrees \n"
     << "    outer stereo angle : " << outerStereo/degree << " degrees \n"
     << "-----------------------------------------------------------\n";
  os.precision(oldprc);

  return os;
}

Here is the call graph for this function:

G4ThreeVector G4Hype::SurfaceNormal ( const G4ThreeVector &  p ) const

virtual

Implements G4VSolid.

Definition at line 309 of file G4Hype.cc.

{
  //
  // Which of the three or four surfaces are we closest to?
  //
  const G4double absZ(std::fabs(p.z()));
  const G4double distZ(absZ - halfLenZ);
  const G4double dist2Z(distZ*distZ);
  
  const G4double xR2( p.x()*p.x()+p.y()*p.y() );
  const G4double dist2Outer( std::fabs(xR2 - HypeOuterRadius2(absZ)) );
  
  if (InnerSurfaceExists())
  {
    //
    // Has inner surface: is this closest?
    //
    const G4double dist2Inner( std::fabs(xR2 - HypeInnerRadius2(absZ)) );
    if (dist2Inner < dist2Z && dist2Inner < dist2Outer)
      return G4ThreeVector( -p.x(), -p.y(), p.z()*tanInnerStereo2 ).unit();
  }

  //
  // Do the "endcaps" win?
  //
  if (dist2Z < dist2Outer) 
    return G4ThreeVector( 0.0, 0.0, p.z() < 0 ? -1.0 : 1.0 );
    
    
  //
  // Outer surface wins
  //
  return G4ThreeVector( p.x(), p.y(), -p.z()*tanOuterStereo2 ).unit();
}

Here is the call graph for this function:

Member Data Documentation

G4double G4Hype::endInnerRadius

protected

Definition at line 178 of file G4Hype.hh.

G4double G4Hype::endInnerRadius2

protected

Definition at line 176 of file G4Hype.hh.

G4double G4Hype::endOuterRadius

protected

Definition at line 179 of file G4Hype.hh.

G4double G4Hype::endOuterRadius2

protected

Definition at line 177 of file G4Hype.hh.

G4double G4Hype::halfLenZ

protected

Definition at line 164 of file G4Hype.hh.

G4double G4Hype::innerRadius

protected

Definition at line 162 of file G4Hype.hh.

G4double G4Hype::innerRadius2

protected

Definition at line 174 of file G4Hype.hh.

G4double G4Hype::innerStereo

protected

Definition at line 165 of file G4Hype.hh.

G4double G4Hype::outerRadius

protected

Definition at line 163 of file G4Hype.hh.

G4double G4Hype::outerRadius2

protected

Definition at line 175 of file G4Hype.hh.

G4double G4Hype::outerStereo

protected

Definition at line 166 of file G4Hype.hh.

G4double G4Hype::tanInnerStereo

protected

Definition at line 170 of file G4Hype.hh.

G4double G4Hype::tanInnerStereo2

protected

Definition at line 172 of file G4Hype.hh.

G4double G4Hype::tanOuterStereo

protected

Definition at line 171 of file G4Hype.hh.

G4double G4Hype::tanOuterStereo2

protected

Definition at line 173 of file G4Hype.hh.

---

The documentation for this class was generated from the following files:

• source/geant4.10.03.p03/source/geometry/solids/specific/include/G4Hype.hh
• source/geant4.10.03.p03/source/geometry/solids/specific/src/G4Hype.cc