Geant4  10.03.p03
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Public Member Functions | List of all members
G4FSALDormandPrince745 Class Reference

#include <G4FSALDormandPrince745.hh>

Inheritance diagram for G4FSALDormandPrince745:
Inheritance graph
[legend]
Collaboration diagram for G4FSALDormandPrince745:
Collaboration graph
[legend]

Public Member Functions

 G4FSALDormandPrince745 (G4EquationOfMotion *EqRhs, G4int numberOfVariables=6, G4bool primary=true)
 
 ~G4FSALDormandPrince745 ()
 
void Stepper (const G4double y[], const G4double dydx[], G4double h, G4double yout[], G4double yerr[], G4double nextDydx[])
 
void interpolate (const G4double yInput[], const G4double dydx[], G4double yOut[], G4double Step, G4double tau)
 
void SetupInterpolate (const G4double yInput[], const G4double dydx[], const G4double Step)
 
void Interpolate (const G4double yInput[], const G4double dydx[], const G4double Step, G4double yOut[], G4double tau)
 
G4double DistChord () const
 
G4int IntegratorOrder () const
 
G4bool isFSAL () const
 
- Public Member Functions inherited from G4VFSALIntegrationStepper
 G4VFSALIntegrationStepper (G4EquationOfMotion *Equation, G4int numIntegrationVariables, G4int numStateVariables=12)
 
virtual ~G4VFSALIntegrationStepper ()
 
virtual void ComputeRightHandSide (const G4double y[], G4double dydx[])
 
void NormaliseTangentVector (G4double vec[6])
 
void NormalisePolarizationVector (G4double vec[12])
 
void RightHandSide (const double y[], double dydx[])
 
G4int GetNumberOfVariables () const
 
G4int GetNumberOfStateVariables () const
 
G4EquationOfMotion * GetEquationOfMotion ()
 
void SetEquationOfMotion (G4EquationOfMotion *newEquation)
 
G4int GetfNoRHSCalls ()
 
void increasefNORHSCalls ()
 
void ResetfNORHSCalls ()
 

Detailed Description

Definition at line 48 of file G4FSALDormandPrince745.hh.

Constructor & Destructor Documentation

G4FSALDormandPrince745::G4FSALDormandPrince745 ( G4EquationOfMotion *  EqRhs,
G4int  numberOfVariables = 6,
G4bool  primary = true 
)

Definition at line 59 of file G4FSALDormandPrince745.cc.

62 : G4VFSALIntegrationStepper(EqRhs, noIntegrationVariables){
63 
64  const G4int numberOfVariables = noIntegrationVariables;
65 
66  //New Chunk of memory being created for use by the stepper
67 
68  //aki - for storing intermediate RHS
69  ak2 = new G4double[numberOfVariables];
70  ak3 = new G4double[numberOfVariables];
71  ak4 = new G4double[numberOfVariables];
72  ak5 = new G4double[numberOfVariables];
73  ak6 = new G4double[numberOfVariables];
74  ak7 = new G4double[numberOfVariables];
75 
76  yTemp = new G4double[numberOfVariables] ;
77  yIn = new G4double[numberOfVariables] ;
78 
79  pseudoDydx_for_DistChord = new G4double[numberOfVariables];
80 
81  fLastInitialVector = new G4double[numberOfVariables] ;
82  fLastFinalVector = new G4double[numberOfVariables] ;
83  fLastDyDx = new G4double[numberOfVariables];
84 
85  fMidVector = new G4double[numberOfVariables];
86  fMidError = new G4double[numberOfVariables];
87  if( primary )
88  {
89  fAuxStepper = new G4FSALDormandPrince745(EqRhs, numberOfVariables,
90  !primary);
91  }
92 }
G4int
int G4int
Definition: G4Types.hh:78
G4FSALDormandPrince745::G4FSALDormandPrince745
G4FSALDormandPrince745(G4EquationOfMotion *EqRhs, G4int numberOfVariables=6, G4bool primary=true)
Definition: G4FSALDormandPrince745.cc:59
G4VFSALIntegrationStepper::G4VFSALIntegrationStepper
G4VFSALIntegrationStepper(G4EquationOfMotion *Equation, G4int numIntegrationVariables, G4int numStateVariables=12)
Definition: G4VFSALIntegrationStepper.cc:33
G4double
double G4double
Definition: G4Types.hh:76
G4FSALDormandPrince745::~G4FSALDormandPrince745 ( )

Definition at line 96 of file G4FSALDormandPrince745.cc.

96  {
97  //clear all previously allocated memory for stepper and DistChord
98  delete[] ak2;
99  delete[] ak3;
100  delete[] ak4;
101  delete[] ak5;
102  delete[] ak6;
103  delete[] ak7;
104 
105  delete[] yTemp;
106  delete[] yIn;
107 
108  delete[] fLastInitialVector;
109  delete[] fLastFinalVector;
110  delete[] fLastDyDx;
111  delete[] fMidVector;
112  delete[] fMidError;
113 
114  delete fAuxStepper;
115 
116  delete[] pseudoDydx_for_DistChord;
117 
118 }

Member Function Documentation

G4double G4FSALDormandPrince745::DistChord ( ) const
virtual

Implements G4VFSALIntegrationStepper.

Definition at line 251 of file G4FSALDormandPrince745.cc.

252 {
253  G4double distLine, distChord;
254  G4ThreeVector initialPoint, finalPoint, midPoint;
255 
256  // Store last initial and final points (they will be overwritten in self-Stepper call!)
257  initialPoint = G4ThreeVector( fLastInitialVector[0],
258  fLastInitialVector[1], fLastInitialVector[2]);
259  finalPoint = G4ThreeVector( fLastFinalVector[0],
260  fLastFinalVector[1], fLastFinalVector[2]);
261 
262  // Do half a step using StepNoErr
263 
264  fAuxStepper->Stepper( fLastInitialVector, fLastDyDx, 0.5 * fLastStepLength,
265  fMidVector, fMidError, pseudoDydx_for_DistChord );
266 
267  midPoint = G4ThreeVector( fMidVector[0], fMidVector[1], fMidVector[2]);
268 
269  // Use stored values of Initial and Endpoint + new Midpoint to evaluate
270  // distance of Chord
271 
272 
273  if (initialPoint != finalPoint)
274  {
275  distLine = G4LineSection::Distline( midPoint, initialPoint, finalPoint );
276  distChord = distLine;
277  }
278  else
279  {
280  distChord = (midPoint-initialPoint).mag();
281  }
282  return distChord;
283 }
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
G4LineSection::Distline
static G4double Distline(const G4ThreeVector &OtherPnt, const G4ThreeVector &LinePntA, const G4ThreeVector &LinePntB)
Definition: G4LineSection.hh:84
G4FSALDormandPrince745::Stepper
void Stepper(const G4double y[], const G4double dydx[], G4double h, G4double yout[], G4double yerr[], G4double nextDydx[])
Definition: G4FSALDormandPrince745.cc:126
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

G4int G4FSALDormandPrince745::IntegratorOrder ( ) const
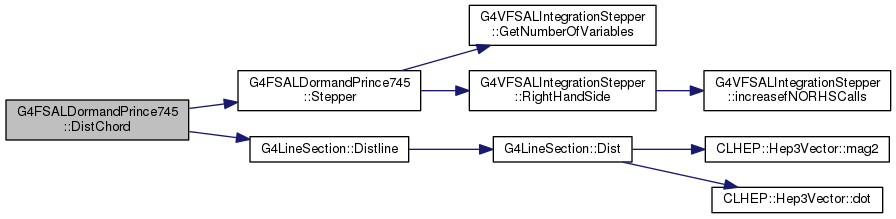
inlinevirtual

Implements G4VFSALIntegrationStepper.

Definition at line 81 of file G4FSALDormandPrince745.hh.

81 {return 4; }
void G4FSALDormandPrince745::interpolate ( const G4double  yInput[],
const G4double  dydx[],
G4double  yOut[],
G4double  Step,
G4double  tau 
)

Definition at line 286 of file G4FSALDormandPrince745.cc.

290  {
291 
292  G4double
293  bf1, bf2, bf3, bf4, bf5, bf6, bf7;
294 
295 
296 
297 
298 
299  const G4int numberOfVariables= this->GetNumberOfVariables();
300 
301  G4double tau0 = tau;
302 
303  for(int i=0;i<numberOfVariables;i++)
304  {
305  yIn[i]=yInput[i];
306  }
307 
308  G4double
309  tau_2 = tau0*tau0 ,
310  tau_3 = tau0*tau_2,
311  tau_4 = tau_2*tau_2;
312 
313  bf1 = (157015080.0*tau_4 - 13107642775.0*tau_3+ 34969693132.0*tau_2- 32272833064.0*tau
314  + 11282082432.0)/11282082432.0,
315  bf2 = 0.0 ,
316  bf3 = - 100.0*tau*(15701508.0*tau_3 - 914128567.0*tau_2 + 2074956840.0*tau
317  - 1323431896.0)/32700410799.0,
318  bf4 = 25.0*tau*(94209048.0*tau_3- 1518414297.0*tau_2+ 2460397220.0*tau - 889289856.0)/5641041216.0 ,
319  bf5 = -2187.0*tau*(52338360.0*tau_3 - 451824525.0*tau_2 + 687873124.0*tau - 259006536.0)/199316789632.0 ,
320  bf6 = 11.0*tau*(106151040.0*tau_3- 661884105.0*tau_2 + 946554244.0*tau - 361440756.0)/2467955532.0 ,
321  bf7 = tau*(1.0 - tau)*(8293050.0*tau_2 - 82437520.0*tau + 44764047.0)/ 29380423.0 ;
322 
323 
324  for( int i=0; i<numberOfVariables; i++){
325  yOut[i] = yIn[i] + Step*tau*(bf1*dydx[i] + bf2*ak2[i] + bf3*ak3[i] + bf4*ak4[i]
326  + bf5*ak5[i] + bf6*ak6[i] + bf7*ak7[i] ) ;
327  }
328 
329 
330 
331 }
G4int
int G4int
Definition: G4Types.hh:78
G4VFSALIntegrationStepper::GetNumberOfVariables
G4int GetNumberOfVariables() const
Step
Definition: Step.hh:41
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

void G4FSALDormandPrince745::Interpolate ( const G4double  yInput[],
const G4double  dydx[],
const G4double  Step,
G4double  yOut[],
G4double  tau 
)

Definition at line 392 of file G4FSALDormandPrince745.cc.

396  {
397  //Define the coefficients for the polynomials
398  G4double bi[10][5], b[10];
399  G4int numberOfVariables = this->GetNumberOfVariables();
400 
401  // COEFFICIENTS OF bi[1]
402  bi[1][0] = 1.0 ,
403  bi[1][1] = -38039.0/7040.0 ,
404  bi[1][2] = 125923.0/10560.0 ,
405  bi[1][3] = -19683.0/1760.0 ,
406  bi[1][4] = 3303.0/880.0 ,
407  // --------------------------------------------------------
408  //
409  // COEFFICIENTS OF bi[2]
410  bi[2][0] = 0.0 ,
411  bi[2][1] = 0.0 ,
412  bi[2][2] = 0.0 ,
413  bi[2][3] = 0.0 ,
414  bi[2][4] = 0.0 ,
415  // --------------------------------------------------------
416  //
417  // COEFFICIENTS OF bi[3]
418  bi[3][0] = 0.0 ,
419  bi[3][1] = -12500.0/4081.0 ,
420  bi[3][2] = 205000.0/12243.0 ,
421  bi[3][3] = -90000.0/4081.0 ,
422  bi[3][4] = 36000.0/4081.0 ,
423  // --------------------------------------------------------
424  //
425  // COEFFICIENTS OF bi[4]
426  bi[4][0] = 0.0 ,
427  bi[4][1] = -3125.0/704.0 ,
428  bi[4][2] = 25625.0/1056.0 ,
429  bi[4][3] = -5625.0/176.0 ,
430  bi[4][4] = 1125.0/88.0 ,
431  // --------------------------------------------------------
432  //
433  // COEFFICIENTS OF bi[5]
434  bi[5][0] = 0.0 ,
435  bi[5][1] = 164025.0/74624.0 ,
436  bi[5][2] = -448335.0/37312.0 ,
437  bi[5][3] = 295245.0/18656.0 ,
438  bi[5][4] = -59049.0/9328.0 ,
439  // --------------------------------------------------------
440  //
441  // COEFFICIENTS OF bi[6]
442  bi[6][0] = 0.0 ,
443  bi[6][1] = -25.0/28.0 ,
444  bi[6][2] = 205.0/42.0 ,
445  bi[6][3] = -45.0/7.0 ,
446  bi[6][4] = 18.0/7.0 ,
447  // --------------------------------------------------------
448  //
449  // COEFFICIENTS OF bi[7]
450  bi[7][0] = 0.0 ,
451  bi[7][1] = -2.0/11.0 ,
452  bi[7][2] = 73.0/55.0 ,
453  bi[7][3] = -171.0/55.0 ,
454  bi[7][4] = 108.0/55.0 ,
455  // --------------------------------------------------------
456  //
457  // COEFFICIENTS OF bi[8]
458  bi[8][0] = 0.0 ,
459  bi[8][1] = 189.0/22.0 ,
460  bi[8][2] = -1593.0/55.0 ,
461  bi[8][3] = 3537.0/110.0 ,
462  bi[8][4] = -648.0/55.0 ,
463  // --------------------------------------------------------
464  //
465  // COEFFICIENTS OF bi[9]
466  bi[9][0] = 0.0 ,
467  bi[9][1] = 351.0/110.0 ,
468  bi[9][2] = -999.0/55.0 ,
469  bi[9][3] = 2943.0/110.0 ,
470  bi[9][4] = -648.0/55.0 ;
471  // --------------------------------------------------------
472 
473 
474 
475  for(G4int i = 0; i< numberOfVariables; i++)
476  yIn[i] = yInput[i];
477 
478  G4double tau0 = tau;
479  // Calculating the polynomials :
480 
481  for(int i=1; i<=9; i++){ //Here i is NOT the coordinate no. , it's stage no.
482  b[i] = 0;
483  tau = 1.0;
484  for(int j=0; j<=4; j++){
485  b[i] += bi[i][j]*tau;
486  tau*=tau0;
487  }
488  }
489 
490  for(int i=0; i<numberOfVariables; i++){ //Here i IS the cooridnate no.
491  yOut[i] = yIn[i] + Step*tau0*(b[1]*dydx[i] + b[2]*ak2[i] + b[3]*ak3[i] +
492  b[4]*ak4[i] + b[5]*ak5[i] + b[6]*ak6[i] +
493  b[7]*ak7[i] + b[8]*ak8[i] + b[9]*ak9[i] );
494  }
495 
496 }
G4int
int G4int
Definition: G4Types.hh:78
test.b
tuple b
Definition: test.py:12
G4VFSALIntegrationStepper::GetNumberOfVariables
G4int GetNumberOfVariables() const
Step
Definition: Step.hh:41
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

G4bool G4FSALDormandPrince745::isFSAL ( ) const
inline

Definition at line 82 of file G4FSALDormandPrince745.hh.

82 { return true; }
void G4FSALDormandPrince745::SetupInterpolate ( const G4double  yInput[],
const G4double  dydx[],
const G4double  Step 
)

Definition at line 333 of file G4FSALDormandPrince745.cc.

335  {
336 
337  //Coefficients for the additional stages :
338  G4double
339  b81 = 6245.0/62208.0 ,
340  b82 = 0.0 ,
341  b83 = 8875.0/103032.0 ,
342  b84 = -125.0/1728.0 ,
343  b85 = 801.0/13568.0 ,
344  b86 = -13519.0/368064.0 ,
345  b87 = 11105.0/368064.0 ,
346 
347  b91 = 632855.0/4478976.0 ,
348  b92 = 0.0 ,
349  b93 = 4146875.0/6491016.0 ,
350  b94 = 5490625.0/14183424.0 ,
351  b95 = -15975.0/108544.0 ,
352  b96 = 8295925.0/220286304.0 ,
353  b97 = -1779595.0/62938944.0 ,
354  b98 = -805.0/4104.0 ;
355 
356  const G4int numberOfVariables= this->GetNumberOfVariables();
357 
358  // Saving yInput because yInput and yOut can be aliases for same array
359  for(int i=0;i<numberOfVariables;i++)
360  {
361  yIn[i]=yInput[i];
362  }
363 
364  yTemp[7] = yIn[7];
365 
366  ak8 = new G4double[numberOfVariables];
367  ak9 = new G4double[numberOfVariables];
368 
369  //Evaluate the extra stages :
370  for(int i=0;i<numberOfVariables;i++)
371  {
372  yTemp[i] = yIn[i] + Step*( b81*dydx[i] + b82*ak2[i] + b83*ak3[i] +
373  b84*ak4[i] + b85*ak5[i] + b86*ak6[i] +
374  b87*ak7[i] );
375  }
376  RightHandSide( yTemp, ak8 ); //8th Stage
377 
378  for(int i=0;i<numberOfVariables;i++)
379  {
380  yTemp[i] = yIn[i] + Step * ( b91*dydx[i] + b92*ak2[i] + b93*ak3[i] +
381  b94*ak4[i] + b95*ak5[i] + b96*ak6[i] +
382  b97*ak7[i] + b98*ak8[i] );
383  }
384  RightHandSide( yTemp, ak9 ); //9th Stage
385 
386 
387 
388 }
G4int
int G4int
Definition: G4Types.hh:78
G4VFSALIntegrationStepper::RightHandSide
void RightHandSide(const double y[], double dydx[])
Definition: G4VFSALIntegrationStepper.cc:60
G4VFSALIntegrationStepper::GetNumberOfVariables
G4int GetNumberOfVariables() const
Step
Definition: Step.hh:41
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

void G4FSALDormandPrince745::Stepper ( const G4double  y[],
const G4double  dydx[],
G4double  h,
G4double  yout[],
G4double  yerr[],
G4double  nextDydx[] 
)
virtual

Implements G4VFSALIntegrationStepper.

Definition at line 126 of file G4FSALDormandPrince745.cc.

133 {
134  G4int i;
135 
136  //The various constants defined on the basis of butcher tableu
137  const G4double //G4double - only once
138  b21 = 0.2 ,
139 
140  b31 = 3.0/40.0, b32 = 9.0/40.0 ,
141 
142  b41 = 44.0/45.0, b42 = -56.0/15.0, b43 = 32.0/9.0,
143 
144  b51 = 19372.0/6561.0, b52 = -25360.0/2187.0, b53 = 64448.0/6561.0,
145  b54 = -212.0/729.0 ,
146 
147  b61 = 9017.0/3168.0 , b62 = -355.0/33.0,
148  b63 = 46732.0/5247.0 , b64 = 49.0/176.0 ,
149  b65 = -5103.0/18656.0 ,
150 
151  b71 = 35.0/384.0, b72 = 0.,
152  b73 = 500.0/1113.0, b74 = 125.0/192.0,
153  b75 = -2187.0/6784.0, b76 = 11.0/84.0,
154 
155 // c1 = 35.0/384.0, c2 = .0,
156 // c3 = 500.0/1113.0, c4 = 125.0/192.0,
157 // c5 = -2187.0/6784.0, c6 = 11.0/84.0,
158 // c7 = 0,
159 
160  dc1 = b71 - 5179.0/57600.0,
161  dc2 = b72 - .0,
162  dc3 = b73 - 7571.0/16695.0,
163  dc4 = b74 - 393.0/640.0,
164  dc5 = b75 + 92097.0/339200.0,
165  dc6 = b76 - 187.0/2100.0,
166  dc7 = - 1.0/40.0 ; //end of declaration
167 
168 
169  const G4int numberOfVariables= this->GetNumberOfVariables();
170  G4double *DyDx = new G4double[numberOfVariables];
171 
172  // The number of variables to be integrated over
173  yOut[7] = yTemp[7] = yIn[7];
174  // Saving yInput because yInput and yOut can be aliases for same array
175 
176  for(i=0;i<numberOfVariables;i++)
177  {
178  yIn[i]=yInput[i];
179  DyDx[i] = dydx[i];
180  }
181 
182 
183 
184  // RightHandSide(yIn, DyDx) ;
185  // 1st Step - Not doing, getting passed
186 
187  for(i=0;i<numberOfVariables;i++)
188  {
189  yTemp[i] = yIn[i] + b21*Step*DyDx[i] ;
190  }
191  RightHandSide(yTemp, ak2) ; // 2nd Step
192 
193  for(i=0;i<numberOfVariables;i++)
194  {
195  yTemp[i] = yIn[i] + Step*(b31*DyDx[i] + b32*ak2[i]) ;
196  }
197  RightHandSide(yTemp, ak3) ; // 3rd Step
198 
199  for(i=0;i<numberOfVariables;i++)
200  {
201  yTemp[i] = yIn[i] + Step*(b41*DyDx[i] + b42*ak2[i] + b43*ak3[i]) ;
202  }
203  RightHandSide(yTemp, ak4) ; // 4th Step
204 
205  for(i=0;i<numberOfVariables;i++)
206  {
207  yTemp[i] = yIn[i] + Step*(b51*DyDx[i] + b52*ak2[i] + b53*ak3[i] +
208  b54*ak4[i]) ;
209  }
210  RightHandSide(yTemp, ak5) ; // 5th Step
211 
212  for(i=0;i<numberOfVariables;i++)
213  {
214  yTemp[i] = yIn[i] + Step*(b61*DyDx[i] + b62*ak2[i] + b63*ak3[i] +
215  b64*ak4[i] + b65*ak5[i]) ;
216  }
217  RightHandSide(yTemp, ak6) ; // 6th Step
218 
219  for(i=0;i<numberOfVariables;i++)
220  {
221  yOut[i] = yIn[i] + Step*(b71*DyDx[i] + b72*ak2[i] + b73*ak3[i] +
222  b74*ak4[i] + b75*ak5[i] + b76*ak6[i]);
223  }
224  RightHandSide(yOut, ak7); //7th and Final step
225 
226  for(i=0;i<numberOfVariables;i++)
227  {
228 
229  yErr[i] = Step*(dc1*DyDx[i] + dc2*ak2[i] + dc3*ak3[i] + dc4*ak4[i] +
230  dc5*ak5[i] + dc6*ak6[i] + dc7*ak7[i] ) ;
231 
232 
233  // Store Input and Final values, for possible use in calculating chord
234  fLastInitialVector[i] = yIn[i] ;
235  fLastFinalVector[i] = yOut[i];
236  fLastDyDx[i] = DyDx[i];
237  nextDydx[i] = ak7[i];
238 
239 
240  }
241 
242  fLastStepLength = Step;
243 
244  return ;
245 }
G4int
int G4int
Definition: G4Types.hh:78
G4VFSALIntegrationStepper::RightHandSide
void RightHandSide(const double y[], double dydx[])
Definition: G4VFSALIntegrationStepper.cc:60
G4VFSALIntegrationStepper::GetNumberOfVariables
G4int GetNumberOfVariables() const
Step
Definition: Step.hh:41
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

Here is the caller graph for this function:

The documentation for this class was generated from the following files: