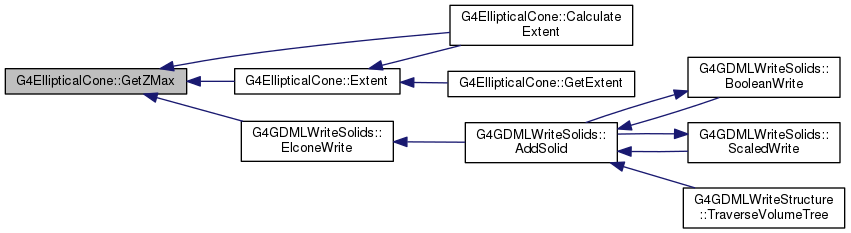
423 if (sigz < halfCarTol)
442 if (
sqr(p.
x()/( xSemiAxis - halfCarTol ))
443 +
sqr(p.
y()/( ySemiAxis - halfCarTol )) <=
sqr( zheight+zTopCut ) )
458 yi = p.
y() + q*v.
y();
463 if (
sqr(xi/xSemiAxis) +
sqr(yi/ySemiAxis) <=
sqr( zheight + zTopCut ) )
468 return (sigz < -halfCarTol) ? q : 0;
470 else if (xi/(xSemiAxis*xSemiAxis)*v.
x()
471 + yi/(ySemiAxis*ySemiAxis)*v.
y() >= 0)
485 sigz = p.
z() - zTopCut;
487 if (sigz > -halfCarTol)
494 if (
sqr(p.
x()/( xSemiAxis - halfCarTol ))
495 +
sqr(p.
y()/( ySemiAxis - halfCarTol )) <=
sqr( zheight-zTopCut ) )
503 yi = p.
y() + q*v.
y();
505 if (
sqr(xi/xSemiAxis) +
sqr(yi/ySemiAxis) <=
sqr( zheight - zTopCut ) )
507 return (sigz > -halfCarTol) ? q : 0;
509 else if (xi/(xSemiAxis*xSemiAxis)*v.
x()
510 + yi/(ySemiAxis*ySemiAxis)*v.
y() >= 0)
529 if (
sqr((lambda*v.
x()+p.
x())/xSemiAxis) +
530 sqr((lambda*v.
y()+p.
y())/ySemiAxis) <=
531 sqr(zTopCut + zheight + 0.5*kRadTolerance) )
533 return distMin = std::fabs(lambda);
544 if (
sqr((lambda*v.
x() + p.
x())/xSemiAxis) +
545 sqr((lambda*v.
y() + p.
y())/ySemiAxis) <=
546 sqr(zheight - zTopCut + 0.5*kRadTolerance) )
548 return distMin = std::fabs(lambda);
552 if (p.
z() > zTopCut - halfCarTol
553 && p.
z() < zTopCut + halfCarTol )
561 if (p.
z() < -zTopCut + halfCarTol
562 && p.
z() > -zTopCut - halfCarTol)
577 v.
y()*p.
y()/
sqr(ySemiAxis) + v.
z()*(zheight-p.
z()));
579 sqr(zheight - p.
z());
585 if ( discr < -halfCarTol )
590 if ( (discr >= - halfCarTol ) && (discr < halfCarTol ) )
592 return distMin = std::fabs(-B/(2.*A));
595 G4double plus = (-B+std::sqrt(discr))/(2.*A);
596 G4double minus = (-B-std::sqrt(discr))/(2.*A);
600 if ( ( std::fabs(plus) < halfCarTol )||( std::fabs(minus) < halfCarTol ) )
603 p.
y()/(ySemiAxis*ySemiAxis),
604 -( p.
z() - zheight ));
605 if ( truenorm*v >= 0)
618 if ( minus > halfCarTol && minus < distMin )
626 pin.
y()/(ySemiAxis*ySemiAxis),
627 - ( pin.
z() - zheight ));
634 if ( plus > halfCarTol && plus < distMin )
642 pin.
y()/(ySemiAxis*ySemiAxis),
643 - ( pin.
z() - zheight ) );
650 if (distMin < halfCarTol) distMin=0.;
static const G4double kInfinity
double B(double temperature)
double A(double temperature)
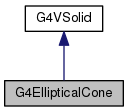
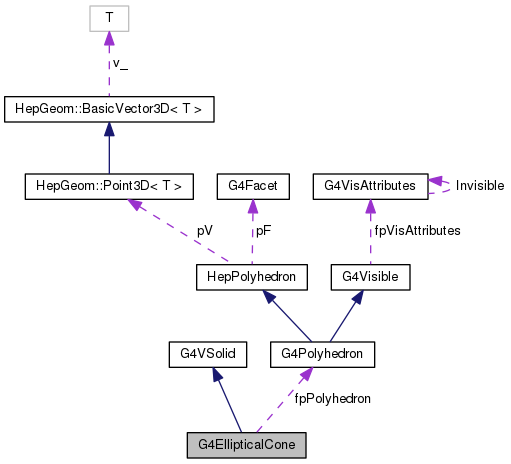
 Protected Attributes inherited from G4VSolid
Protected Attributes inherited from G4VSolid Protected Member Functions inherited from G4VSolid
Protected Member Functions inherited from G4VSolid