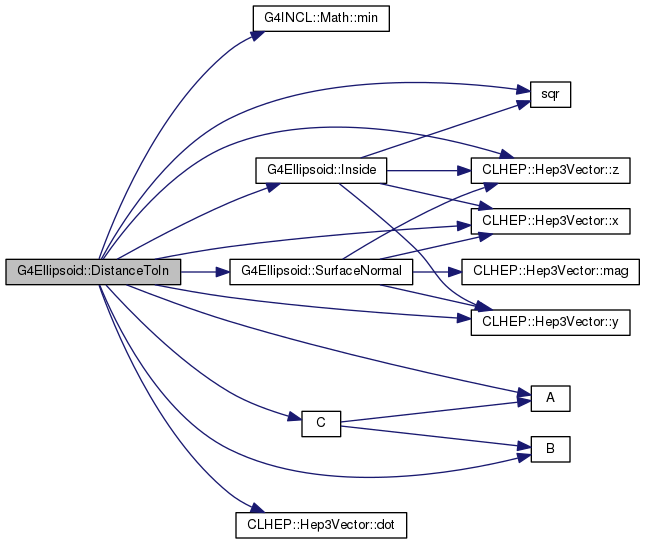
336 if (p.
z() <= zBottomCut+halfCarTolerance)
338 if (v.
z() <= 0.0) {
return distMin; }
339 G4double distZ = (zBottomCut - p.
z()) / v.
z();
341 if ( (distZ > -halfRadTolerance) && (
Inside(p+distZ*v) !=
kOutside) )
344 if ( std::fabs(distZ) < halfRadTolerance ) { distZ=0.; }
345 return distMin= distZ;
348 if (p.
z() >= zTopCut-halfCarTolerance)
350 if (v.z() >= 0.0) {
return distMin;}
351 G4double distZ = (zTopCut - p.
z()) / v.z();
352 if ( (distZ > -halfRadTolerance) && (
Inside(p+distZ*v) !=
kOutside) )
355 if ( std::fabs(distZ) < halfRadTolerance ) { distZ=0.; }
356 return distMin= distZ;
364 A=
sqr(v.x()/xSemiAxis) +
sqr(v.y()/ySemiAxis) +
sqr(v.z()/zSemiAxis);
365 C=
sqr(p.
x()/xSemiAxis) +
sqr(p.
y()/ySemiAxis) +
sqr(p.
z()/zSemiAxis) - 1.0;
366 B= 2.0 * ( p.
x()*v.x()/(xSemiAxis*xSemiAxis)
367 + p.
y()*v.y()/(ySemiAxis*ySemiAxis)
368 + p.
z()*v.z()/(zSemiAxis*zSemiAxis) );
373 G4double distR= (-B - std::sqrt(C)) / (2.0*A);
375 if ( (distR > halfRadTolerance)
376 && (intZ >= zBottomCut-halfRadTolerance)
377 && (intZ <= zTopCut+halfRadTolerance) )
381 else if( (distR >- halfRadTolerance)
382 && (intZ >= zBottomCut-halfRadTolerance)
383 && (intZ <= zTopCut+halfRadTolerance) )
389 distR = (-B + std::sqrt(C) ) / (2.0*A);
390 if(distR>0.) { distMin=0.; }
394 distR= (-B + std::sqrt(C)) / (2.0*A);
395 intZ = p.
z()+distR*v.z();
396 if ( (distR > halfRadTolerance)
397 && (intZ >= zBottomCut-halfRadTolerance)
398 && (intZ <= zTopCut+halfRadTolerance) )
401 if (norm.
dot(v)<0.) { distMin = distR; }
404 if ( (distMin!=
kInfinity) && (distMin>dRmax) )
407 G4double fTerm = distMin-std::fmod(distMin,dRmax);
412 if (std::fabs(distMin)<halfRadTolerance) { distMin=0.; }
static const G4double kInfinity
double dot(const Hep3Vector &) const
EInside Inside(const G4ThreeVector &p) const
double B(double temperature)
double A(double temperature)
G4double DistanceToIn(const G4ThreeVector &p, const G4ThreeVector &v) const
G4ThreeVector SurfaceNormal(const G4ThreeVector &p) const
T min(const T t1, const T t2)
brief Return the smallest of the two arguments
 Protected Attributes inherited from G4VSolid
Protected Attributes inherited from G4VSolid Protected Member Functions inherited from G4VSolid
Protected Member Functions inherited from G4VSolid