#include <Stat.h>
- Author
Definition at line 51 of file Stat.h.
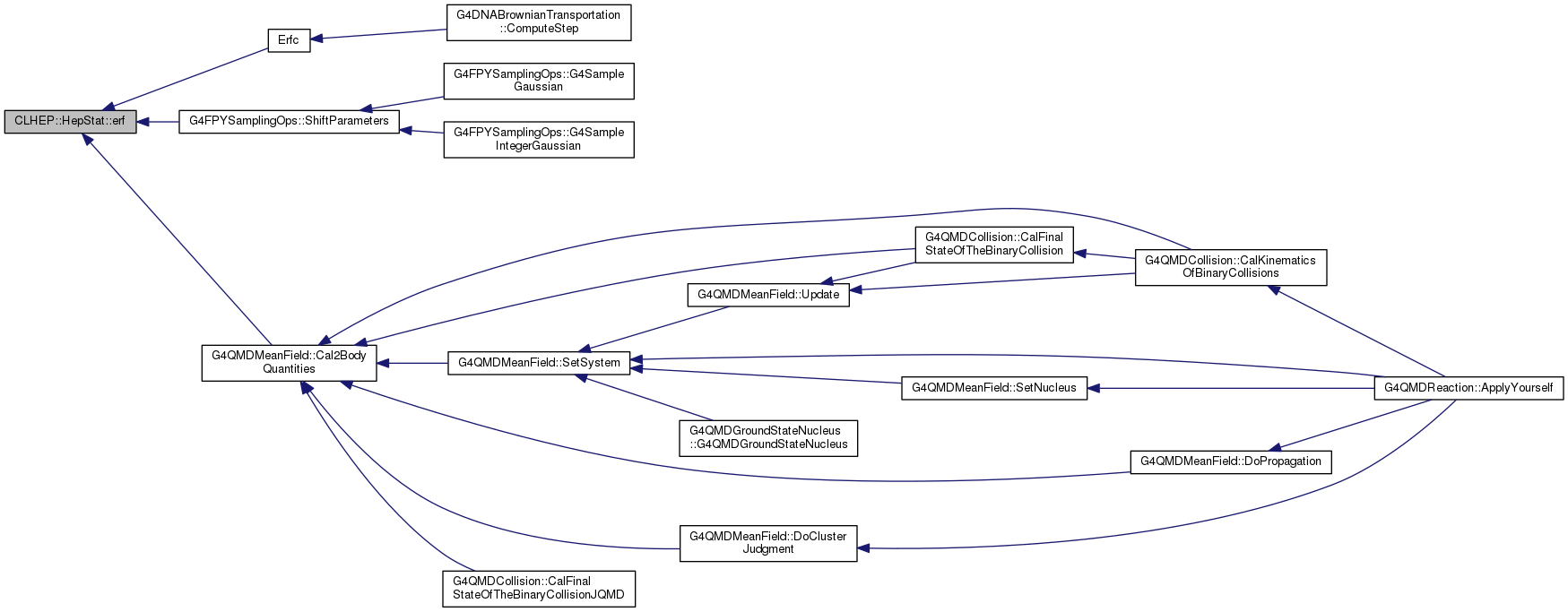
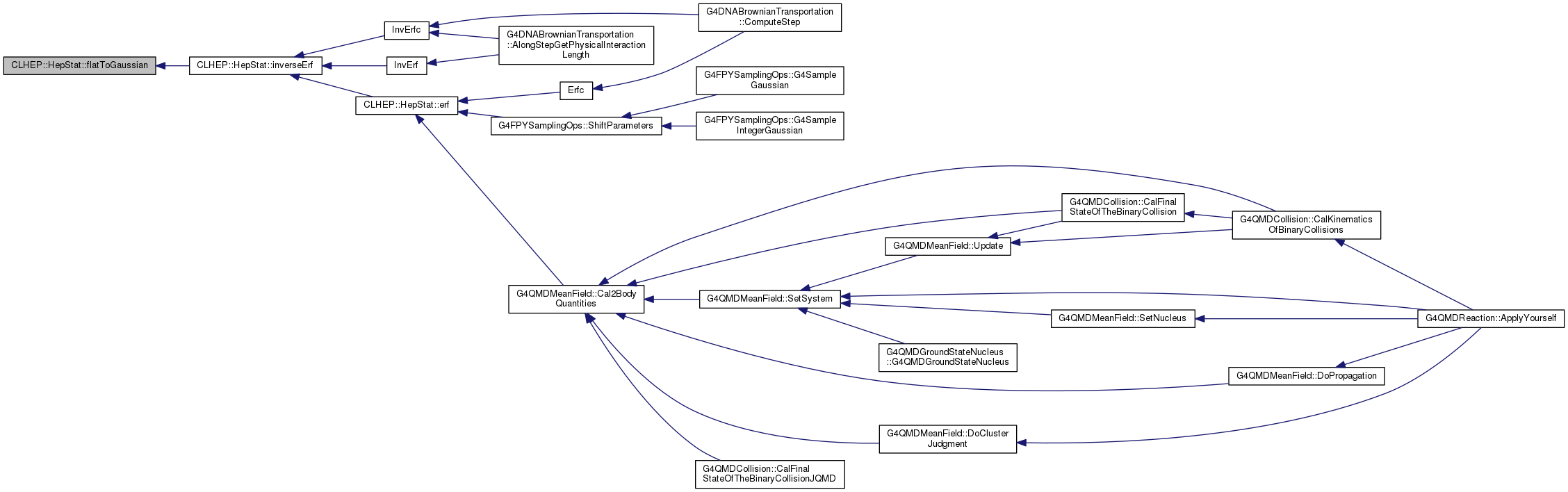
| double CLHEP::HepStat::erf |
( |
double |
x | ) |
|
|
static |
Definition at line 269 of file flatToGaussian.cc.
294 double deriv = std::exp(-
x*
x) * (2.0 / std::sqrt(
CLHEP::pi));
static double inverseErf(double t)
static double erfQ(double x)
static constexpr double pi
| double CLHEP::HepStat::erfQ |
( |
double |
x | ) |
|
|
static |
Definition at line 24 of file erfQ.cc.
35 erfc= t*std::exp(-z*z-1.26551223+t*(1.00002368+t*(0.37409196+t*(0.09678418+
36 t*(-0.18628806+t*(0.27886807+t*(-1.13520398+t*(1.48851587+
37 t*(-0.82215223+t*0.17087277 ))) ))) )));
41 if (
x < 0 ) erfc = 2.0 - erfc;
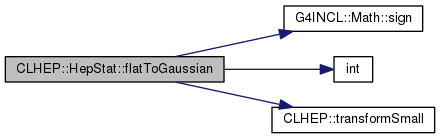
| double CLHEP::HepStat::flatToGaussian |
( |
double |
r | ) |
|
|
static |
Definition at line 89 of file flatToGaussian.cc.
95 std::cout <<
"r = " << r <<
"\n";
102 std::cout <<
"r = " << r <<
"sign negative \n";
104 }
else if ( r == .5 ) {
119 const double* tptr = 0;
131 if (index <= 0) index = 1;
136 std::cout <<
"index = " << index <<
" dx = " << dx <<
" h = " << h <<
"\n";
143 std::cout <<
"offset index = " << index <<
"\n";
148 }
else if (r <
Tsteps[0]) {
155 for (
int tableN = 3; tableN >= 0; tableN-- ) {
156 if ( r <
Tsteps[tableN] ) {
continue;}
158 std::cout <<
"Using table " << tableN <<
"\n";
160 double step =
Tsteps[tableN];
166 if (index == 0) index = 1;
167 if (index >=
Tsizes[tableN]) index =
Tsizes[tableN] - 1;
171 std::cout <<
"index = " << index <<
" dx = " << dx <<
" h = " << h <<
"\n";
173 index = (index<<1) +
Toffsets[tableN] - 2;
193 std::cout <<
"y0: " << y0 <<
" y1: " << y1 <<
" d0: " << d0 <<
" d1: " << d1 <<
"\n";
197 double oneMinusX = 1 - dx;
198 double oneMinusX2 = oneMinusX * oneMinusX;
200 double f0 = (2. * dx + 1.) * oneMinusX2;
201 double f1 = (3. - 2. * dx) * x2;
202 double g0 = h * dx * oneMinusX2;
203 double g1 = - h * oneMinusX * x2;
206 std::cout <<
"f0: " << f0 <<
" f1: " << f1 <<
" g0: " << g0 <<
" g1: " << g1 <<
"\n";
209 double answer = f0 * y0 + f1 * y1 + g0 * d0 + g1 *
d1;
212 std::cout <<
"variate is: " << sign*answer <<
"\n";
215 return sign * answer;
static const double Tsteps[5]
typedef int(XMLCALL *XML_NotStandaloneHandler)(void *userData)
static const int Toffsets[5]
static const double gaussTables[2 *TableSize]
static const int Tsizes[5]
double transformSmall(double r)
| double CLHEP::HepStat::gammln |
( |
double |
x | ) |
|
|
static |
Definition at line 19 of file gammln.cc.
28 static const double cof[6] = {76.18009172947146,-86.50532032941677,
29 24.01409824083091, -1.231739572450155,
30 0.1208650973866179e-2, -0.5395239384953e-5};
34 tmp -= (x + 0.5) * std::log(tmp);
35 double ser = 1.000000000190015;
37 for ( j = 0; j <= 5; j++ ) {
41 return -tmp + std::log(2.5066282746310005*ser);
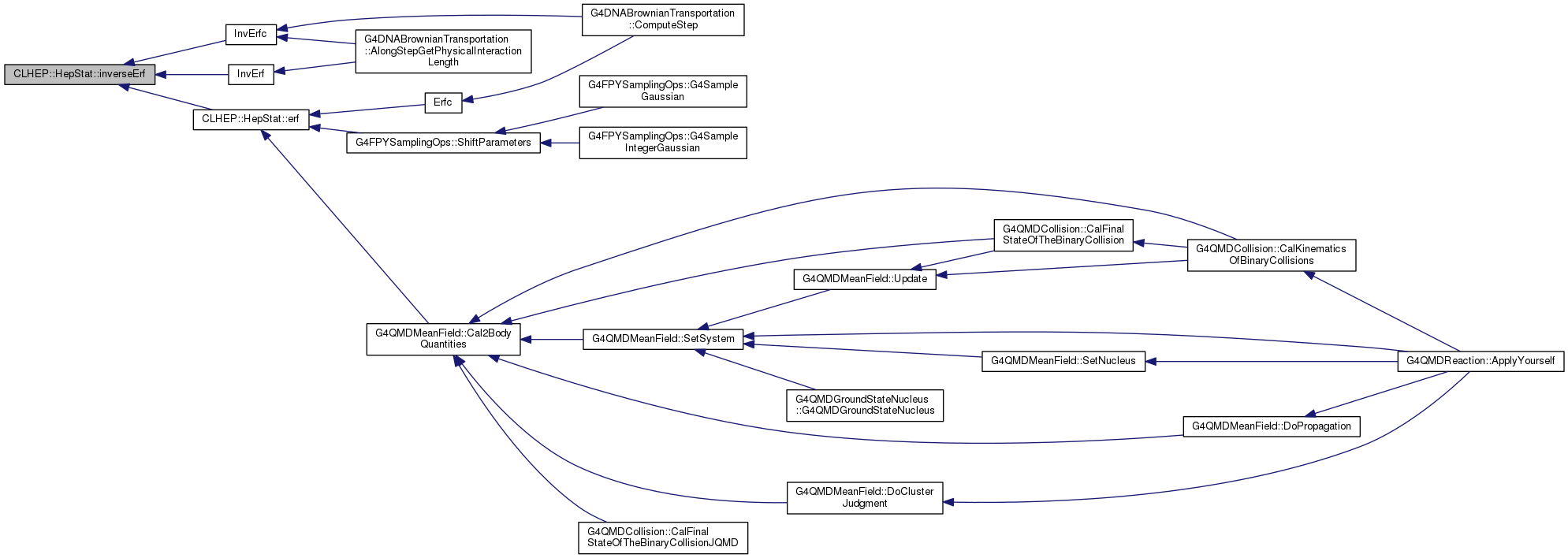
| double CLHEP::HepStat::inverseErf |
( |
double |
t | ) |
|
|
static |
The documentation for this class was generated from the following files:
- source/geant4.10.03.p03/source/externals/clhep/include/CLHEP/Random/Stat.h
- source/geant4.10.03.p03/source/externals/clhep/src/erfQ.cc
- source/geant4.10.03.p03/source/externals/clhep/src/flatToGaussian.cc
- source/geant4.10.03.p03/source/externals/clhep/src/gammln.cc