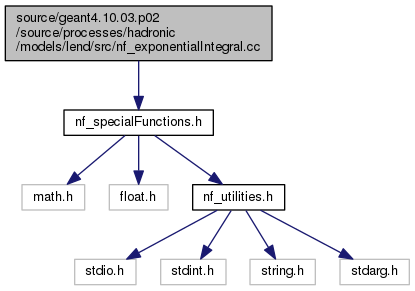
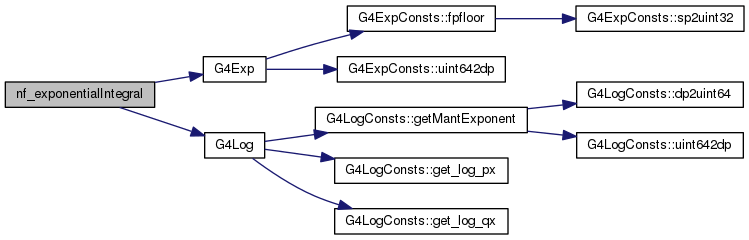
Go to the source code of this file.
|
| #define | EULER 0.57721566490153286 /* Euler's constant gamma */ |
| |
| #define | MAXIT 100 /* Maximum allowed number of iterations. */ |
| |
| #define | FPMIN 1.0e-300 /* close to the smallest representable floting-point number. */ |
| |
| #define | EPS 1.0e-15 /* Desired relative error, not smaller than the machine precision. */ |
| |
| #define EPS 1.0e-15 /* Desired relative error, not smaller than the machine precision. */ |
| #define EULER 0.57721566490153286 /* Euler's constant gamma */ |
| #define FPMIN 1.0e-300 /* close to the smallest representable floting-point number. */ |
| #define MAXIT 100 /* Maximum allowed number of iterations. */ |
| double nf_exponentialIntegral |
( |
int |
n, |
|
|
double |
x, |
|
|
nfu_status * |
status |
|
) |
| |
Definition at line 28 of file nf_exponentialIntegral.cc.
31 double a,
b,
c, d, del, fact, h, psi;
39 if( (
n < 0 ) || (
x < 0.0 ) || ( (
x == 0.0 ) && ( (
n == 0 ) || (
n == 1 ) ) ) ) {
51 for( i = 1; i <=
MAXIT; i++ ) {
54 d = 1.0 / ( a * d +
b );
58 if( fabs( del - 1.0 ) <
EPS )
return( h *
G4Exp( -
x ) );
64 for( i = 1; i <=
MAXIT; i++ ) {
67 del = -fact / ( i - nm1 ); }
70 for( ii = 1; ii <= nm1; ii++ ) psi += 1.0 / ii;
71 del = fact * ( -
G4Log(
x ) + psi );
74 if( fabs( del ) < fabs( ans ) *
EPS )
return( ans );
std::vector< ExP01TrackerHit * > a
G4double G4Log(G4double x)
G4double G4Exp(G4double initial_x)
Exponential Function double precision.