#include <G4TriangularFacet.hh>

Inheritance diagram for G4TriangularFacet:

Collaboration diagram for G4TriangularFacet:

Public Member Functions
	G4TriangularFacet ()

	~G4TriangularFacet ()

	G4TriangularFacet (const G4ThreeVector &vt0, const G4ThreeVector &vt1, const G4ThreeVector &vt2, G4FacetVertexType)

	G4TriangularFacet (const G4TriangularFacet &right)

G4TriangularFacet &	operator= (const G4TriangularFacet &right)

G4VFacet *	GetClone ()

G4TriangularFacet *	GetFlippedFacet ()

G4ThreeVector	Distance (const G4ThreeVector &p)

G4double	Distance (const G4ThreeVector &p, G4double minDist)

G4double	Distance (const G4ThreeVector &p, G4double minDist, const G4bool outgoing)

G4double	Extent (const G4ThreeVector axis)

G4bool	Intersect (const G4ThreeVector &p, const G4ThreeVector &v, const G4bool outgoing, G4double &distance, G4double &distFromSurface, G4ThreeVector &normal)

G4double	GetArea () const

G4ThreeVector	GetPointOnFace () const

G4ThreeVector	GetSurfaceNormal () const

void	SetSurfaceNormal (G4ThreeVector normal)

G4GeometryType	GetEntityType () const

G4bool	IsDefined () const

G4int	GetNumberOfVertices () const

G4ThreeVector	GetVertex (G4int i) const

void	SetVertex (G4int i, const G4ThreeVector &val)

G4ThreeVector	GetCircumcentre () const

G4double	GetRadius () const

G4int	AllocatedMemory ()

G4int	GetVertexIndex (G4int i) const

void	SetVertexIndex (G4int i, G4int j)

void	SetVertices (std::vector< G4ThreeVector > *v)

Public Member Functions inherited from G4VFacet
virtual	~G4VFacet ()

G4bool	operator== (const G4VFacet &right) const

void	ApplyTranslation (const G4ThreeVector v)

std::ostream &	StreamInfo (std::ostream &os) const

G4bool	IsInside (const G4ThreeVector &p) const

Additional Inherited Members
Static Protected Attributes inherited from G4VFacet
static const G4double	dirTolerance = 1.0E-14

static const G4double	kCarTolerance

Detailed Description

Definition at line 65 of file G4TriangularFacet.hh.

Constructor & Destructor Documentation

G4TriangularFacet::G4TriangularFacet ( )

Definition at line 167 of file G4TriangularFacet.cc.

   : fSqrDist(0.)
 {
   fVertices = new vector<G4ThreeVector>(3);
   G4ThreeVector zero(0,0,0);
   SetVertex(0, zero);
   SetVertex(1, zero);
   SetVertex(2, zero);
   for (G4int i = 0; i < 3; ++i) fIndices[i] = -1;
   fIsDefined = false;
   fSurfaceNormal.set(0,0,0);
   fA = fB = fC = 0;
   fE1 = zero;
   fE2 = zero;
   fDet = 0.0;
   fArea = fRadius = 0.0;
 }

Here is the call graph for this function:

Here is the caller graph for this function:

G4TriangularFacet::~G4TriangularFacet ( )

Definition at line 187 of file G4TriangularFacet.cc.

 {
   SetVertices(0);
 }

Here is the call graph for this function:

G4TriangularFacet::G4TriangularFacet	(	const G4ThreeVector &	vt0,
		const G4ThreeVector &	vt1,
		const G4ThreeVector &	vt2,
		G4FacetVertexType	vertexType
	)

Definition at line 79 of file G4TriangularFacet.cc.

   : fSqrDist(0.)
 {
   fVertices = new vector<G4ThreeVector>(3);
 
   SetVertex(0, vt0);
   if (vertexType == ABSOLUTE)
   {
     SetVertex(1, vt1);
     SetVertex(2, vt2);
     fE1 = vt1 - vt0;
     fE2 = vt2 - vt0;
   }
   else
   {
     SetVertex(1, vt0 + vt1);
     SetVertex(2, vt0 + vt2);
     fE1 = vt1;
     fE2 = vt2;
   }
 
   G4ThreeVector E1xE2 = fE1.cross(fE2);
   fArea = 0.5 * E1xE2.mag();
   for (G4int i = 0; i < 3; ++i) fIndices[i] = -1;
 
   fIsDefined = true;
   G4double delta = kCarTolerance; // Set tolerance for checking
 
   // Check length of edges
   //
   G4double leng1 = fE1.mag();
   G4double leng2 = (fE2-fE1).mag();
   G4double leng3 = fE2.mag();
   if (leng1 <= delta || leng2 <= delta || leng3 <= delta) 
   {
     fIsDefined = false;
   }
 
   // Check min height of triangle
   //
   if (fIsDefined)
   {
     if (2.*fArea/std::max(std::max(leng1,leng2),leng3) <= delta)
     {
       fIsDefined = false;
     } 
   }
 
   // Define facet
   //
   if (!fIsDefined)
   {
     ostringstream message;
     message << "Facet is too small or too narrow." << G4endl
             << "Triangle area = " << fArea << G4endl
             << "P0 = " << GetVertex(0) << G4endl
             << "P1 = " << GetVertex(1) << G4endl
             << "P2 = " << GetVertex(2) << G4endl
             << "Side1 length (P0->P1) = " << leng1 << G4endl
             << "Side2 length (P1->P2) = " << leng2 << G4endl
             << "Side3 length (P2->P0) = " << leng3;
     G4Exception("G4TriangularFacet::G4TriangularFacet()",
         "GeomSolids1001", JustWarning, message);
     fSurfaceNormal.set(0,0,0);
     fA = fB = fC = 0.0;
     fDet = 0.0;
     fCircumcentre = vt0 + 0.5*fE1 + 0.5*fE2;
     fArea = fRadius = 0.0;
   }
   else
   { 
     fSurfaceNormal = E1xE2.unit();
     fA   = fE1.mag2();
     fB   = fE1.dot(fE2);
     fC   = fE2.mag2();
     fDet = std::fabs(fA*fC - fB*fB);
 
     fCircumcentre = 
       vt0 + (E1xE2.cross(fE1)*fC + fE2.cross(E1xE2)*fA) / (2.*E1xE2.mag2());
     fRadius = (fCircumcentre - vt0).mag();
   }
 }

Here is the call graph for this function:

G4TriangularFacet::G4TriangularFacet ( const G4TriangularFacet & right )

Definition at line 208 of file G4TriangularFacet.cc.

   : G4VFacet(rhs)
 {
   CopyFrom(rhs);
 }

Member Function Documentation

G4int G4TriangularFacet::AllocatedMemory ( )

inlinevirtual

Implements G4VFacet.

Definition at line 165 of file G4TriangularFacet.hh.

 {
   G4int size = sizeof(*this);
   size += GetNumberOfVertices() * sizeof(G4ThreeVector);
   return size;
 }

Here is the call graph for this function:

G4ThreeVector G4TriangularFacet::Distance ( const G4ThreeVector & p )

Definition at line 268 of file G4TriangularFacet.cc.

 {
   G4ThreeVector D  = GetVertex(0) - p;
   G4double d = fE1.dot(D);
   G4double e = fE2.dot(D);
   G4double f = D.mag2();
   G4double q = fB*e - fC*d;
   G4double t = fB*d - fA*e;
   fSqrDist = 0.;
 
   if (q+t <= fDet)
   {
     if (q < 0.0)
     {
       if (t < 0.0)
       {
         //
         // We are in region 4.
         //
         if (d < 0.0)
         {
           t = 0.0;
           if (-d >= fA) {q = 1.0; fSqrDist = fA + 2.0*d + f;}
           else         {q = -d/fA; fSqrDist = d*q + f;}
         }
         else
         {
           q = 0.0;
           if       (e >= 0.0) {t = 0.0; fSqrDist = f;}
           else if (-e >= fC)   {t = 1.0; fSqrDist = fC + 2.0*e + f;}
           else                {t = -e/fC; fSqrDist = e*t + f;}
         }
       }
       else
       {
         //
         // We are in region 3.
         //
         q = 0.0;
         if      (e >= 0.0) {t = 0.0; fSqrDist = f;}
         else if (-e >= fC)  {t = 1.0; fSqrDist = fC + 2.0*e + f;}
         else               {t = -e/fC; fSqrDist = e*t + f;}
       }
     }
     else if (t < 0.0)
     {
       //
       // We are in region 5.
       //
       t = 0.0;
       if      (d >= 0.0) {q = 0.0; fSqrDist = f;}
       else if (-d >= fA)  {q = 1.0; fSqrDist = fA + 2.0*d + f;}
       else               {q = -d/fA; fSqrDist = d*q + f;}
     }
     else
     {
       //
       // We are in region 0.
       //
       q       = q / fDet;
       t       = t / fDet;
       fSqrDist = q*(fA*q + fB*t + 2.0*d) + t*(fB*q + fC*t + 2.0*e) + f;
     }
   }
   else
   {
     if (q < 0.0)
     {
       //
       // We are in region 2.
       //
       G4double tmp0 = fB + d;
       G4double tmp1 = fC + e;
       if (tmp1 > tmp0)
       {
         G4double numer = tmp1 - tmp0;
         G4double denom = fA - 2.0*fB + fC;
         if (numer >= denom) {q = 1.0; t = 0.0; fSqrDist = fA + 2.0*d + f;}
         else
         {
           q       = numer/denom;
           t       = 1.0 - q;
           fSqrDist = q*(fA*q + fB*t +2.0*d) + t*(fB*q + fC*t + 2.0*e) + f;
         }
       }
       else
       {
         q = 0.0;
         if      (tmp1 <= 0.0) {t = 1.0; fSqrDist = fC + 2.0*e + f;}
         else if (e >= 0.0)    {t = 0.0; fSqrDist = f;}
         else                  {t = -e/fC; fSqrDist = e*t + f;}
       }
     }
     else if (t < 0.0)
     {
       //
       // We are in region 6.
       //
       G4double tmp0 = fB + e;
       G4double tmp1 = fA + d;
       if (tmp1 > tmp0)
       {
         G4double numer = tmp1 - tmp0;
         G4double denom = fA - 2.0*fB + fC;
         if (numer >= denom) {t = 1.0; q = 0.0; fSqrDist = fC + 2.0*e + f;}
         else
         {
           t       = numer/denom;
           q       = 1.0 - t;
           fSqrDist = q*(fA*q + fB*t +2.0*d) + t*(fB*q + fC*t + 2.0*e) + f;
         }
       }
       else
       {
         t = 0.0;
         if      (tmp1 <= 0.0) {q = 1.0; fSqrDist = fA + 2.0*d + f;}
         else if (d >= 0.0)    {q = 0.0; fSqrDist = f;}
         else                  {q = -d/fA; fSqrDist = d*q + f;}
       }
     }
     else
       //
       // We are in region 1.
       //
     {
       G4double numer = fC + e - fB - d;
       if (numer <= 0.0)
       {
         q       = 0.0;
         t       = 1.0;
         fSqrDist = fC + 2.0*e + f;
       }
       else
       {
         G4double denom = fA - 2.0*fB + fC;
         if (numer >= denom) {q = 1.0; t = 0.0; fSqrDist = fA + 2.0*d + f;}
         else
         {
           q       = numer/denom;
           t       = 1.0 - q;
           fSqrDist = q*(fA*q + fB*t + 2.0*d) + t*(fB*q + fC*t + 2.0*e) + f;
         }
       }
     }
   } 
   //
   //
   // Do fA check for rounding errors in the distance-squared.  It appears that
   // the conventional methods for calculating fSqrDist breaks down when very
   // near to or at the surface (as required by transport).
   // We'll therefore also use the magnitude-squared of the vector displacement.
   // (Note that I've also tried to get around this problem by using the
   // existing equations for
   //
   //    fSqrDist = function(fA,fB,fC,d,q,t)
   //
   // and use fA more accurate addition process which minimises errors and
   // breakdown of cummutitivity [where (A+B)+C != A+(B+C)] but this still
   // doesn't work.
   // Calculation from u = D + q*fE1 + t*fE2 is less efficient, but appears
   // more robust.
   //
   if (fSqrDist < 0.0) fSqrDist = 0.;
   G4ThreeVector u = D + q*fE1 + t*fE2;
   G4double u2 = u.mag2();
   //
   // The following (part of the roundoff error check) is from Oliver Merle'q
   // updates.
   //
   if (fSqrDist > u2) fSqrDist = u2;
 
   return u;
 }

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4TriangularFacet::Distance	(	const G4ThreeVector &	p,
		G4double	minDist
	)

virtual

Implements G4VFacet.

Definition at line 452 of file G4TriangularFacet.cc.

 {
   //
   // Start with quicky test to determine if the surface of the sphere enclosing
   // the triangle is any closer to p than minDist.  If not, then don't bother
   // about more accurate test.
   //
   G4double dist = kInfinity;
   if ((p-fCircumcentre).mag()-fRadius < minDist)
   {
     //
     // It's possible that the triangle is closer than minDist,
     // so do more accurate assessment.
     //
     dist = Distance(p).mag();
   }
   return dist;
 }

Here is the call graph for this function:

G4double G4TriangularFacet::Distance	(	const G4ThreeVector &	p,
		G4double	minDist,
		const G4bool	outgoing
	)

virtual

Implements G4VFacet.

Definition at line 487 of file G4TriangularFacet.cc.

 {
   //
   // Start with quicky test to determine if the surface of the sphere enclosing
   // the triangle is any closer to p than minDist.  If not, then don't bother
   // about more accurate test.
   //
   G4double dist = kInfinity;
   if ((p-fCircumcentre).mag()-fRadius < minDist)
   {
     //
     // It's possible that the triangle is closer than minDist,
     // so do more accurate assessment.
     //
     G4ThreeVector v  = Distance(p);
     G4double dist1 = sqrt(fSqrDist);
     G4double dir = v.dot(fSurfaceNormal);
     G4bool wrongSide = (dir > 0.0 && !outgoing) || (dir < 0.0 && outgoing);
     if (dist1 <= kCarTolerance)
     {
       //
       // Point p is very close to triangle.  Check if it's on the wrong side,
       // in which case return distance of 0.0 otherwise .
       //
       if (wrongSide) dist = 0.0;
       else dist = dist1;
     }
     else if (!wrongSide) dist = dist1;
   }
   return dist;
 }

Here is the call graph for this function:

G4double G4TriangularFacet::Extent ( const G4ThreeVector axis )

virtual

Implements G4VFacet.

Definition at line 528 of file G4TriangularFacet.cc.

 {
   G4double ss = GetVertex(0).dot(axis);
   G4double sp = GetVertex(1).dot(axis);
   if (sp > ss) ss = sp;
   sp = GetVertex(2).dot(axis);
   if (sp > ss) ss = sp;
   return ss;
 }

Here is the call graph for this function:

G4double G4TriangularFacet::GetArea ( ) const

virtual

Implements G4VFacet.

Definition at line 771 of file G4TriangularFacet.cc.

 {
   return fArea;
 }

Here is the caller graph for this function:

G4ThreeVector G4TriangularFacet::GetCircumcentre ( ) const

inlinevirtual

Implements G4VFacet.

Definition at line 155 of file G4TriangularFacet.hh.

 {
   return fCircumcentre;
 }

G4VFacet * G4TriangularFacet::GetClone ( )

virtual

Implements G4VFacet.

Definition at line 233 of file G4TriangularFacet.cc.

 {
   G4TriangularFacet *fc =
     new G4TriangularFacet (GetVertex(0), GetVertex(1), GetVertex(2), ABSOLUTE);
   return fc;
 }

Here is the call graph for this function:

G4GeometryType G4TriangularFacet::GetEntityType ( ) const

virtual

Implements G4VFacet.

Definition at line 778 of file G4TriangularFacet.cc.

 {
   return "G4TriangularFacet";
 }

G4TriangularFacet * G4TriangularFacet::GetFlippedFacet ( )

Definition at line 247 of file G4TriangularFacet.cc.

 {
   G4TriangularFacet *flipped =
     new G4TriangularFacet (GetVertex(0), GetVertex(1), GetVertex(2), ABSOLUTE);
   return flipped;
 }

Here is the call graph for this function:

G4int G4TriangularFacet::GetNumberOfVertices ( ) const

inlinevirtual

Implements G4VFacet.

Definition at line 139 of file G4TriangularFacet.hh.

 {
   return 3;
 }

Here is the caller graph for this function:

G4ThreeVector G4TriangularFacet::GetPointOnFace ( ) const

virtual

Implements G4VFacet.

Definition at line 757 of file G4TriangularFacet.cc.

 {
   G4double u = G4UniformRand();
   G4double v = G4UniformRand();
   if (u+v > 1.) { u = 1. - u; v = 1. - v; }
   return GetVertex(0) + u*fE1 + v*fE2;
 }

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4TriangularFacet::GetRadius ( ) const

inlinevirtual

Implements G4VFacet.

Definition at line 160 of file G4TriangularFacet.hh.

 {
   return fRadius;
 }

G4ThreeVector G4TriangularFacet::GetSurfaceNormal ( ) const

virtual

Implements G4VFacet.

Definition at line 785 of file G4TriangularFacet.cc.

 {
   return fSurfaceNormal;
 }

Here is the caller graph for this function:

G4ThreeVector G4TriangularFacet::GetVertex ( G4int i ) const

inlinevirtual

Implements G4VFacet.

Definition at line 144 of file G4TriangularFacet.hh.

 {      
   G4int indice = fIndices[i];
   return indice < 0 ? (*fVertices)[i] : (*fVertices)[indice];
 }

Here is the caller graph for this function:

G4int G4TriangularFacet::GetVertexIndex ( G4int i ) const

inlinevirtual

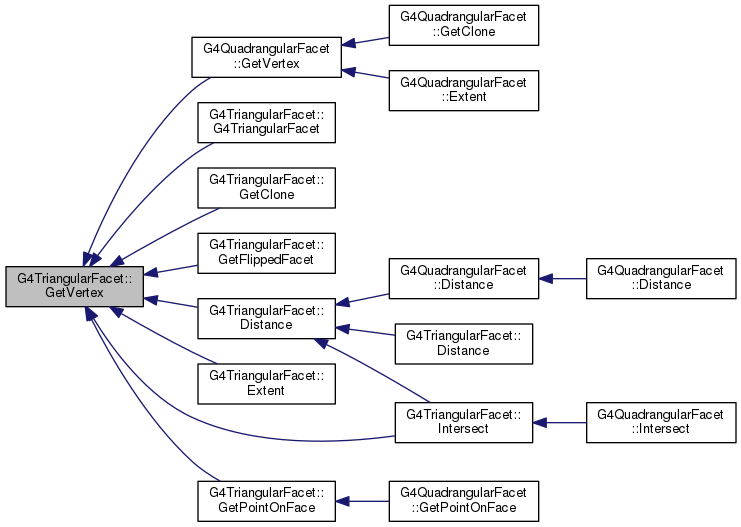
Implements G4VFacet.

Definition at line 172 of file G4TriangularFacet.hh.

 {
   if (i < 3) return fIndices[i];
   else       return 999999999;
 }

G4bool G4TriangularFacet::Intersect	(	const G4ThreeVector &	p,
		const G4ThreeVector &	v,
		const G4bool	outgoing,
		G4double &	distance,
		G4double &	distFromSurface,
		G4ThreeVector &	normal
	)

virtual

Implements G4VFacet.

Definition at line 565 of file G4TriangularFacet.cc.

 {
   //
   // Check whether the direction of the facet is consistent with the vector v
   // and the need to be outgoing or ingoing.  If inconsistent, disregard and
   // return false.
   //
   G4double w = v.dot(fSurfaceNormal);
   if ((outgoing && w < -dirTolerance) || (!outgoing && w > dirTolerance))
   {
     distance = kInfinity;
     distFromSurface = kInfinity;
     normal.set(0,0,0);
     return false;
   } 
   //
   // Calculate the orthogonal distance from p to the surface containing the
   // triangle.  Then determine if we're on the right or wrong side of the
   // surface (at fA distance greater than kCarTolerance to be consistent with
   // "outgoing".
   //
   const G4ThreeVector &p0 = GetVertex(0);
   G4ThreeVector D  = p0 - p;
   distFromSurface  = D.dot(fSurfaceNormal);
   G4bool wrongSide = (outgoing && distFromSurface < -0.5*kCarTolerance) ||
     (!outgoing && distFromSurface >  0.5*kCarTolerance);
  
   if (wrongSide)
   {
     distance = kInfinity;
     distFromSurface = kInfinity;
     normal.set(0,0,0);
     return false;
   }
 
   wrongSide = (outgoing && distFromSurface < 0.0)
            || (!outgoing && distFromSurface > 0.0);
   if (wrongSide)
   {
     //
     // We're slightly on the wrong side of the surface.  Check if we're close
     // enough using fA precise distance calculation.
     //
     G4ThreeVector u = Distance(p);
     if (fSqrDist <= kCarTolerance*kCarTolerance)
     {
       //
       // We're very close.  Therefore return fA small negative number
       // to pretend we intersect.
       //
       // distance = -0.5*kCarTolerance
       distance = 0.0;
       normal = fSurfaceNormal;
       return true;
     }
     else
     {
       //
       // We're close to the surface containing the triangle, but sufficiently
       // far from the triangle, and on the wrong side compared to the directions
       // of the surface normal and v.  There is no intersection.
       //
       distance = kInfinity;
       distFromSurface = kInfinity;
       normal.set(0,0,0);
       return false;
     }
   }
   if (w < dirTolerance && w > -dirTolerance)
   {
     //
     // The ray is within the plane of the triangle. Project the problem into 2D
     // in the plane of the triangle. First try to create orthogonal unit vectors
     // mu and nu, where mu is fE1/|fE1|.  This is kinda like
     // the original algorithm due to Rickard Holmberg, but with better
     // mathematical justification than the original method ... however,
     // beware Rickard's was less time-consuming.
     //
     // Note that vprime is not fA unit vector.  We need to keep it unnormalised
     // since the values of distance along vprime (s0 and s1) for intersection
     // with the triangle will be used to determine if we cut the plane at the
     // same time.
     //
     G4ThreeVector mu = fE1.unit();
     G4ThreeVector nu = fSurfaceNormal.cross(mu);
     G4TwoVector pprime(p.dot(mu), p.dot(nu));
     G4TwoVector vprime(v.dot(mu), v.dot(nu));
     G4TwoVector P0prime(p0.dot(mu), p0.dot(nu));
     G4TwoVector E0prime(fE1.mag(), 0.0);
     G4TwoVector E1prime(fE2.dot(mu), fE2.dot(nu));
     G4TwoVector loc[2];
     if (G4TessellatedGeometryAlgorithms::IntersectLineAndTriangle2D(pprime,
                                     vprime, P0prime, E0prime, E1prime, loc))
     {
       //
       // There is an intersection between the line and triangle in 2D.
       // Now check which part of the line intersects with the plane
       // containing the triangle in 3D.
       //
       G4double vprimemag = vprime.mag();
       G4double s0        = (loc[0] - pprime).mag()/vprimemag;
       G4double s1        = (loc[1] - pprime).mag()/vprimemag;
       G4double normDist0 = fSurfaceNormal.dot(s0*v) - distFromSurface;
       G4double normDist1 = fSurfaceNormal.dot(s1*v) - distFromSurface;
 
       if ((normDist0 < 0.0 && normDist1 < 0.0)
        || (normDist0 > 0.0 && normDist1 > 0.0)
        || (normDist0 == 0.0 && normDist1 == 0.0) ) 
       {
         distance        = kInfinity;
         distFromSurface = kInfinity;
         normal.set(0,0,0);
         return false;
       }
       else
       {
         G4double dnormDist = normDist1 - normDist0;
         if (fabs(dnormDist) < DBL_EPSILON)
         {
           distance = s0;
           normal   = fSurfaceNormal;
           if (!outgoing) distFromSurface = -distFromSurface;
           return true;
         }
         else
         {
           distance = s0 - normDist0*(s1-s0)/dnormDist;
           normal   = fSurfaceNormal;
           if (!outgoing) distFromSurface = -distFromSurface;
           return true;
         }
       }
     }
     else
     {
       distance = kInfinity;
       distFromSurface = kInfinity;
       normal.set(0,0,0);
       return false;
     }
   }
   //
   //
   // Use conventional algorithm to determine the whether there is an
   // intersection.  This involves determining the point of intersection of the
   // line with the plane containing the triangle, and then calculating if the
   // point is within the triangle.
   //
   distance = distFromSurface / w;
   G4ThreeVector pp = p + v*distance;
   G4ThreeVector DD = p0 - pp;
   G4double d = fE1.dot(DD);
   G4double e = fE2.dot(DD);
   G4double ss = fB*e - fC*d;
   G4double t = fB*d - fA*e;
 
   G4double sTolerance = (fabs(fB)+ fabs(fC) + fabs(d) + fabs(e))*kCarTolerance;
   G4double tTolerance = (fabs(fA)+ fabs(fB) + fabs(d) + fabs(e))*kCarTolerance;
   G4double detTolerance = (fabs(fA)+ fabs(fC) + 2*fabs(fB) )*kCarTolerance;
 
   //if (ss < 0.0 || t < 0.0 || ss+t > fDet)
   if (ss < -sTolerance || t < -tTolerance || ( ss+t - fDet ) > detTolerance)
   {
     //
     // The intersection is outside of the triangle.
     //
     distance = distFromSurface = kInfinity;
     normal.set(0,0,0);
     return false;
   }
   else
   {
     //
     // There is an intersection.  Now we only need to set the surface normal.
     //
     normal = fSurfaceNormal;
     if (!outgoing) distFromSurface = -distFromSurface;
     return true;
   }
 }

Here is the call graph for this function:

Here is the caller graph for this function:

G4bool G4TriangularFacet::IsDefined ( ) const

inlinevirtual

Implements G4VFacet.

Definition at line 134 of file G4TriangularFacet.hh.

 {
   return fIsDefined;
 }

Here is the caller graph for this function:

G4TriangularFacet & G4TriangularFacet::operator= ( const G4TriangularFacet & right )

Definition at line 217 of file G4TriangularFacet.cc.

 {
   SetVertices(0);
 
   if (this != &rhs)
     CopyFrom(rhs);
 
   return *this;
 }

Here is the call graph for this function:

void G4TriangularFacet::SetSurfaceNormal ( G4ThreeVector normal )

Definition at line 792 of file G4TriangularFacet.cc.

 {
   fSurfaceNormal = normal;
 }

Here is the call graph for this function:

void G4TriangularFacet::SetVertex	(	G4int	i,
		const G4ThreeVector &	val
	)

inlinevirtual

Implements G4VFacet.

Definition at line 150 of file G4TriangularFacet.hh.

 {
   (*fVertices)[i] = val;
 }

Here is the caller graph for this function:

void G4TriangularFacet::SetVertexIndex	(	G4int	i,
		G4int	j
	)

inlinevirtual

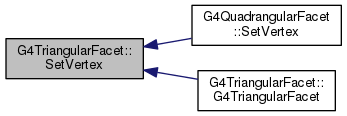
Implements G4VFacet.

Definition at line 178 of file G4TriangularFacet.hh.

 {
   fIndices[i] = j;
 }

void G4TriangularFacet::SetVertices ( std::vector< G4ThreeVector > * v )

inlinevirtual

Implements G4VFacet.

Definition at line 183 of file G4TriangularFacet.hh.

 {
   if (fIndices[0] < 0 && fVertices)
   {
     delete fVertices;
     fVertices = 0;
   }
   fVertices = v;
 }

Here is the caller graph for this function:

The documentation for this class was generated from the following files:

source/geant4.10.03.p02/source/geometry/solids/specific/include/G4TriangularFacet.hh
source/geant4.10.03.p02/source/geometry/solids/specific/src/G4TriangularFacet.cc

Public Member Functions

Additional Inherited Members

Detailed Description

Constructor & Destructor Documentation

Member Function Documentation