|
Geant4
10.03.p02
|
|
Geant4
10.03.p02
|
#include <G4OTubs.hh>
Protected Types | |
| enum | ESide { kNull, kRMin, kRMax, kSPhi, kEPhi, kPZ, kMZ } |
| enum | ENorm { kNRMin, kNRMax, kNSPhi, kNEPhi, kNZ } |
Protected Member Functions | |
| void | Initialize () |
| void | CheckSPhiAngle (G4double sPhi) |
| void | CheckDPhiAngle (G4double dPhi) |
| void | CheckPhiAngles (G4double sPhi, G4double dPhi) |
| void | InitializeTrigonometry () |
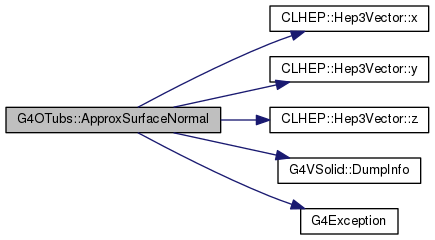
| virtual G4ThreeVector | ApproxSurfaceNormal (const G4ThreeVector &p) const |
 Protected Member Functions inherited from G4CSGSolid Protected Member Functions inherited from G4CSGSolid | |
| G4double | GetRadiusInRing (G4double rmin, G4double rmax) const |
 Protected Member Functions inherited from G4VSolid Protected Member Functions inherited from G4VSolid | |
| void | CalculateClippedPolygonExtent (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const |
| void | ClipCrossSection (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const |
| void | ClipBetweenSections (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const |
| void | ClipPolygon (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis) const |
Protected Attributes | |
| G4double | kRadTolerance |
| G4double | kAngTolerance |
| G4double | fRMin |
| G4double | fRMax |
| G4double | fDz |
| G4double | fSPhi |
| G4double | fDPhi |
| G4double | sinCPhi |
| G4double | cosCPhi |
| G4double | cosHDPhiOT |
| G4double | cosHDPhiIT |
| G4double | sinSPhi |
| G4double | cosSPhi |
| G4double | sinEPhi |
| G4double | cosEPhi |
| G4bool | fPhiFullTube |
| G4double | halfCarTolerance |
| G4double | halfRadTolerance |
| G4double | halfAngTolerance |
 Protected Attributes inherited from G4CSGSolid Protected Attributes inherited from G4CSGSolid | |
| G4double | fCubicVolume |
| G4double | fSurfaceArea |
| G4bool | fRebuildPolyhedron |
| G4Polyhedron * | fpPolyhedron |
 Protected Attributes inherited from G4VSolid Protected Attributes inherited from G4VSolid | |
| G4double | kCarTolerance |
Definition at line 49 of file G4OTubs.hh.
|
protected |
| Enumerator | |
|---|---|
| kNRMin | |
| kNRMax | |
| kNSPhi | |
| kNEPhi | |
| kNZ | |
Definition at line 171 of file G4OTubs.hh.
|
protected |
| Enumerator | |
|---|---|
| kNull | |
| kRMin | |
| kRMax | |
| kSPhi | |
| kEPhi | |
| kPZ | |
| kMZ | |
Definition at line 167 of file G4OTubs.hh.
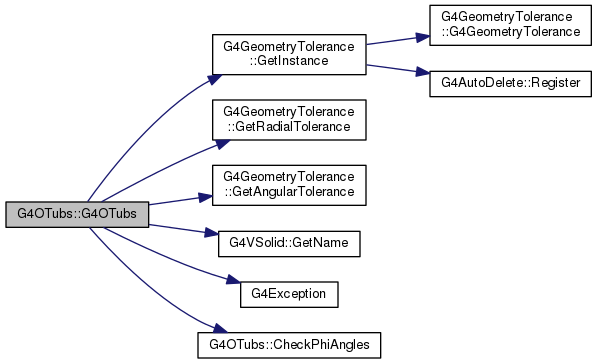
| G4OTubs::G4OTubs | ( | const G4String & | pName, |
| G4double | pRMin, | ||
| G4double | pRMax, | ||
| G4double | pDz, | ||
| G4double | pSPhi, | ||
| G4double | pDPhi | ||
| ) |
Definition at line 59 of file G4OTubs.cc.

|
virtual |
Definition at line 113 of file G4OTubs.cc.
| G4OTubs::G4OTubs | ( | __void__ & | a | ) |
Definition at line 98 of file G4OTubs.cc.
| G4OTubs::G4OTubs | ( | const G4OTubs & | rhs | ) |
Definition at line 121 of file G4OTubs.cc.
|
protectedvirtual |
Reimplemented in G4CutTubs.
Definition at line 581 of file G4OTubs.cc.

|
virtual |
Implements G4VSolid.
Definition at line 213 of file G4OTubs.cc.
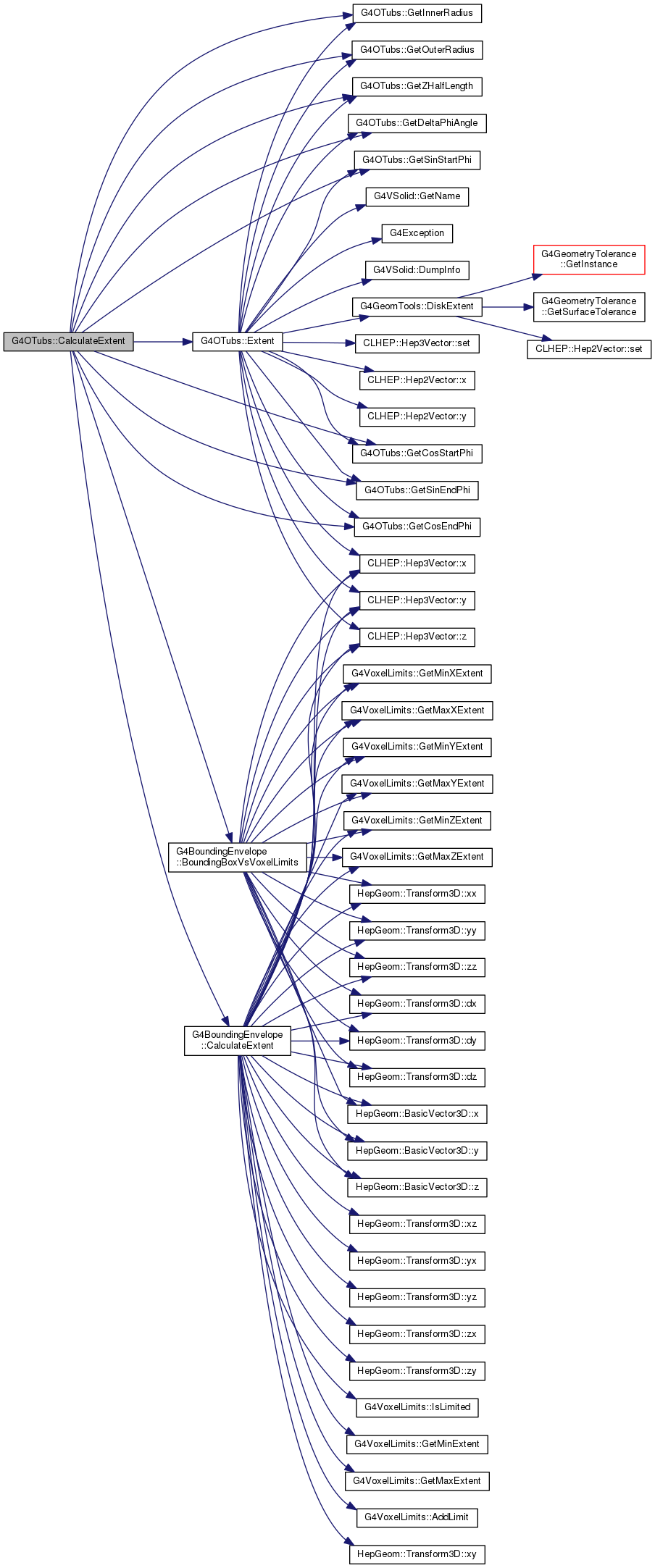

|
virtual |
Reimplemented from G4VSolid.
Definition at line 1621 of file G4OTubs.cc.
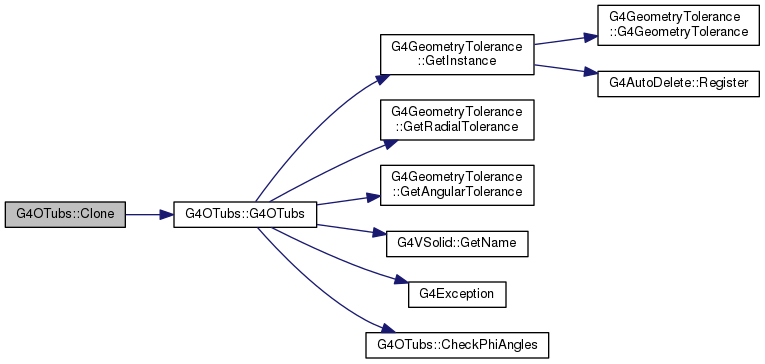
|
virtual |
Reimplemented from G4VSolid.
Definition at line 1728 of file G4OTubs.cc.

|
virtual |
Implements G4VSolid.
Definition at line 1723 of file G4OTubs.cc.

|
virtual |
Implements G4VSolid.
Definition at line 713 of file G4OTubs.cc.

|
virtual |
Implements G4VSolid.
Definition at line 1089 of file G4OTubs.cc.
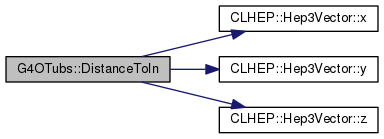
|
virtual |
Implements G4VSolid.
Definition at line 1133 of file G4OTubs.cc.
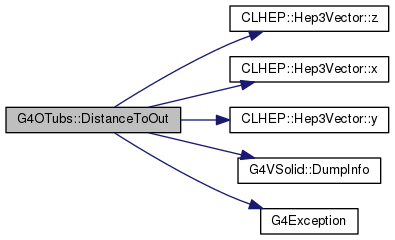
|
virtual |
Implements G4VSolid.
Definition at line 1552 of file G4OTubs.cc.
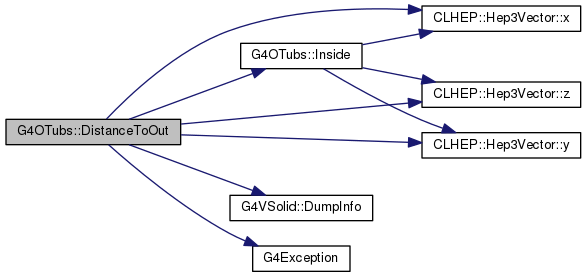
|
virtual |
Reimplemented from G4VSolid.
Definition at line 171 of file G4OTubs.cc.
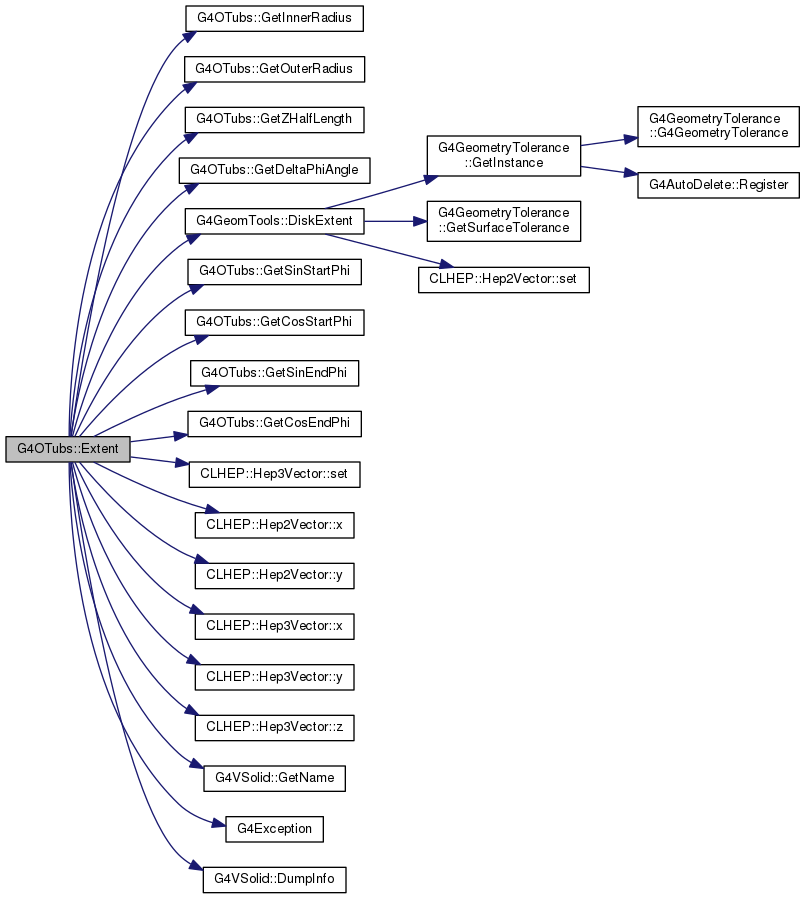

|
inline |
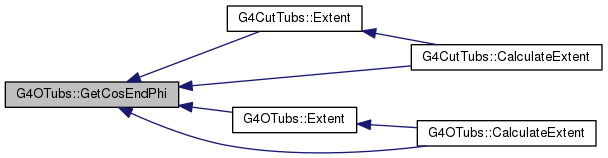
|
inline |
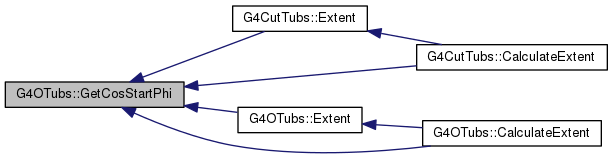
|
inline |

|
inline |
|
inline |
|
virtual |
Implements G4VSolid.
Definition at line 1612 of file G4OTubs.cc.
|
inline |
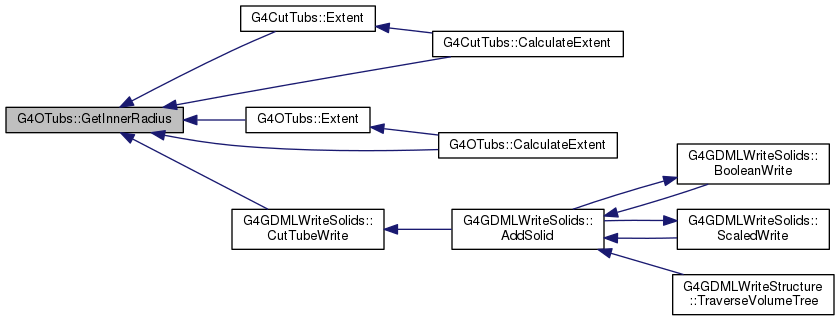
|
inline |
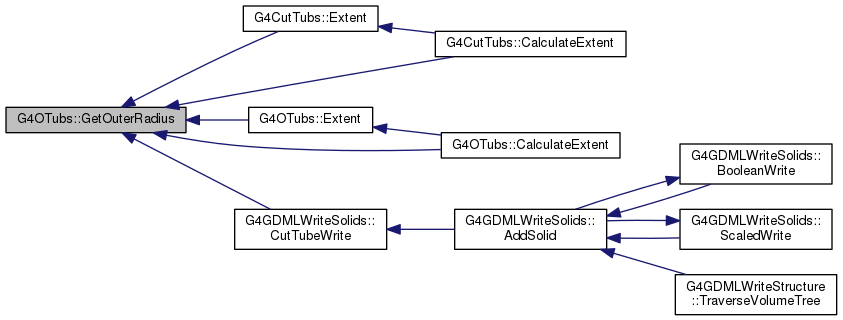
|
virtual |
Reimplemented from G4VSolid.
Definition at line 1653 of file G4OTubs.cc.

|
inline |
|
inline |
|
inline |
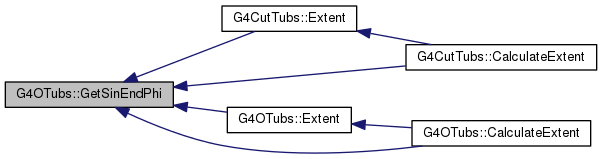
|
inline |
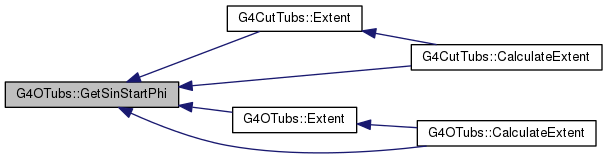
|
inline |
|
inline |
|
inline |

|
inlineprotected |
|
inlineprotected |
|
virtual |
Implements G4VSolid.
Definition at line 323 of file G4OTubs.cc.


Definition at line 140 of file G4OTubs.cc.


|
virtual |
Reimplemented from G4CSGSolid.
Definition at line 1630 of file G4OTubs.cc.

|
virtual |
Implements G4VSolid.
Definition at line 490 of file G4OTubs.cc.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 177 of file G4OTubs.hh.
|
protected |
Definition at line 177 of file G4OTubs.hh.
|
protected |
Definition at line 186 of file G4OTubs.hh.
|
protected |
Definition at line 177 of file G4OTubs.hh.
|
protected |
Definition at line 177 of file G4OTubs.hh.
|
protected |
Definition at line 177 of file G4OTubs.hh.
|
protected |
Definition at line 190 of file G4OTubs.hh.
|
protected |
Definition at line 190 of file G4OTubs.hh.
|
protected |
Definition at line 190 of file G4OTubs.hh.
|
protected |
Definition at line 173 of file G4OTubs.hh.
|
protected |
Definition at line 173 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.
|
protected |
Definition at line 181 of file G4OTubs.hh.