Geant4  10.03.p02
 All Classes Namespaces Files Functions Variables Typedefs Enumerations Enumerator Friends Macros Groups Pages
Public Member Functions | List of all members
G4Cons Class Reference

#include <G4Cons.hh>

Inheritance diagram for G4Cons:
Inheritance graph
[legend]
Collaboration diagram for G4Cons:
Collaboration graph
[legend]

Public Member Functions

 G4Cons (const G4String &pName, G4double pRmin1, G4double pRmax1, G4double pRmin2, G4double pRmax2, G4double pDz, G4double pSPhi, G4double pDPhi)
 
 ~G4Cons ()
 
G4double GetInnerRadiusMinusZ () const
 
G4double GetOuterRadiusMinusZ () const
 
G4double GetInnerRadiusPlusZ () const
 
G4double GetOuterRadiusPlusZ () const
 
G4double GetZHalfLength () const
 
G4double GetStartPhiAngle () const
 
G4double GetDeltaPhiAngle () const
 
G4double GetSinStartPhi () const
 
G4double GetCosStartPhi () const
 
G4double GetSinEndPhi () const
 
G4double GetCosEndPhi () const
 
void SetInnerRadiusMinusZ (G4double Rmin1)
 
void SetOuterRadiusMinusZ (G4double Rmax1)
 
void SetInnerRadiusPlusZ (G4double Rmin2)
 
void SetOuterRadiusPlusZ (G4double Rmax2)
 
void SetZHalfLength (G4double newDz)
 
void SetStartPhiAngle (G4double newSPhi, G4bool trig=true)
 
void SetDeltaPhiAngle (G4double newDPhi)
 
G4double GetCubicVolume ()
 
G4double GetSurfaceArea ()
 
void ComputeDimensions (G4VPVParameterisation *p, const G4int n, const G4VPhysicalVolume *pRep)
 
void Extent (G4ThreeVector &pMin, G4ThreeVector &pMax) const
 
G4bool CalculateExtent (const EAxis pAxis, const G4VoxelLimits &pVoxelLimit, const G4AffineTransform &pTransform, G4double &pMin, G4double &pMax) const
 
EInside Inside (const G4ThreeVector &p) const
 
G4ThreeVector SurfaceNormal (const G4ThreeVector &p) const
 
G4double DistanceToIn (const G4ThreeVector &p, const G4ThreeVector &v) const
 
G4double DistanceToIn (const G4ThreeVector &p) const
 
G4double DistanceToOut (const G4ThreeVector &p, const G4ThreeVector &v, const G4bool calcNorm=G4bool(false), G4bool *validNorm=0, G4ThreeVector *n=0) const
 
G4double DistanceToOut (const G4ThreeVector &p) const
 
G4GeometryType GetEntityType () const
 
G4ThreeVector GetPointOnSurface () const
 
G4VSolid * Clone () const
 
std::ostream & StreamInfo (std::ostream &os) const
 
void DescribeYourselfTo (G4VGraphicsScene &scene) const
 
G4Polyhedron * CreatePolyhedron () const
 
 G4Cons (__void__ &)
 
 G4Cons (const G4Cons &rhs)
 
G4Cons & operator= (const G4Cons &rhs)
 
G4double GetRmin1 () const
 
G4double GetRmax1 () const
 
G4double GetRmin2 () const
 
G4double GetRmax2 () const
 
G4double GetDz () const
 
G4double GetSPhi () const
 
G4double GetDPhi () const
 
- Public Member Functions inherited from G4CSGSolid
 G4CSGSolid (const G4String &pName)
 
virtual ~G4CSGSolid ()
 
virtual G4Polyhedron * GetPolyhedron () const
 
 G4CSGSolid (__void__ &)
 
 G4CSGSolid (const G4CSGSolid &rhs)
 
G4CSGSolid & operator= (const G4CSGSolid &rhs)
 
- Public Member Functions inherited from G4VSolid
 G4VSolid (const G4String &name)
 
virtual ~G4VSolid ()
 
G4bool operator== (const G4VSolid &s) const
 
G4String GetName () const
 
void SetName (const G4String &name)
 
G4double GetTolerance () const
 
void DumpInfo () const
 
virtual G4VisExtent GetExtent () const
 
virtual const G4VSolid * GetConstituentSolid (G4int no) const
 
virtual G4VSolid * GetConstituentSolid (G4int no)
 
virtual const G4DisplacedSolid * GetDisplacedSolidPtr () const
 
virtual G4DisplacedSolid * GetDisplacedSolidPtr ()
 
 G4VSolid (__void__ &)
 
 G4VSolid (const G4VSolid &rhs)
 
G4VSolid & operator= (const G4VSolid &rhs)
 
G4double EstimateCubicVolume (G4int nStat, G4double epsilon) const
 
G4double EstimateSurfaceArea (G4int nStat, G4double ell) const
 

Additional Inherited Members

- Protected Member Functions inherited from G4CSGSolid
G4double GetRadiusInRing (G4double rmin, G4double rmax) const
 
- Protected Member Functions inherited from G4VSolid
void CalculateClippedPolygonExtent (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
 
void ClipCrossSection (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
 
void ClipBetweenSections (G4ThreeVectorList *pVertices, const G4int pSectionIndex, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis, G4double &pMin, G4double &pMax) const
 
void ClipPolygon (G4ThreeVectorList &pPolygon, const G4VoxelLimits &pVoxelLimit, const EAxis pAxis) const
 
- Protected Attributes inherited from G4CSGSolid
G4double fCubicVolume
 
G4double fSurfaceArea
 
G4bool fRebuildPolyhedron
 
G4Polyhedron * fpPolyhedron
 
- Protected Attributes inherited from G4VSolid
G4double kCarTolerance
 

Detailed Description

Definition at line 83 of file G4Cons.hh.

Constructor & Destructor Documentation

G4Cons::G4Cons ( const G4String &  pName,
G4double  pRmin1,
G4double  pRmax1,
G4double  pRmin2,
G4double  pRmax2,
G4double  pDz,
G4double  pSPhi,
G4double  pDPhi 
)

Definition at line 87 of file G4Cons.cc.

92  : G4CSGSolid(pName), fRmin1(pRmin1), fRmin2(pRmin2),
93  fRmax1(pRmax1), fRmax2(pRmax2), fDz(pDz), fSPhi(0.), fDPhi(0.)
94 {
95  kRadTolerance = G4GeometryTolerance::GetInstance()->GetRadialTolerance();
96  kAngTolerance = G4GeometryTolerance::GetInstance()->GetAngularTolerance();
97 
98  halfCarTolerance=kCarTolerance*0.5;
99  halfRadTolerance=kRadTolerance*0.5;
100  halfAngTolerance=kAngTolerance*0.5;
101 
102  // Check z-len
103  //
104  if ( pDz < 0 )
105  {
106  std::ostringstream message;
107  message << "Invalid Z half-length for Solid: " << GetName() << G4endl
108  << " hZ = " << pDz;
109  G4Exception("G4Cons::G4Cons()", "GeomSolids0002",
110  FatalException, message);
111  }
112 
113  // Check radii
114  //
115  if (((pRmin1>=pRmax1) || (pRmin2>=pRmax2) || (pRmin1<0)) && (pRmin2<0))
116  {
117  std::ostringstream message;
118  message << "Invalid values of radii for Solid: " << GetName() << G4endl
119  << " pRmin1 = " << pRmin1 << ", pRmin2 = " << pRmin2
120  << ", pRmax1 = " << pRmax1 << ", pRmax2 = " << pRmax2;
121  G4Exception("G4Cons::G4Cons()", "GeomSolids0002",
122  FatalException, message) ;
123  }
124  if( (pRmin1 == 0.0) && (pRmin2 > 0.0) ) { fRmin1 = 1e3*kRadTolerance ; }
125  if( (pRmin2 == 0.0) && (pRmin1 > 0.0) ) { fRmin2 = 1e3*kRadTolerance ; }
126 
127  // Check angles
128  //
129  CheckPhiAngles(pSPhi, pDPhi);
130 }
G4VSolid::GetName
G4String GetName() const
G4GeometryTolerance::GetRadialTolerance
G4double GetRadialTolerance() const
Definition: G4GeometryTolerance.cc:97
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
G4CSGSolid::G4CSGSolid
G4CSGSolid(const G4String &pName)
Definition: G4CSGSolid.cc:49
FatalException
Definition: G4ExceptionSeverity.hh:60
G4endl
#define G4endl
Definition: G4ios.hh:61
G4VSolid::kCarTolerance
G4double kCarTolerance
Definition: G4VSolid.hh:307
G4GeometryTolerance::GetAngularTolerance
G4double GetAngularTolerance() const
Definition: G4GeometryTolerance.cc:92
G4GeometryTolerance::GetInstance
static G4GeometryTolerance * GetInstance()
Definition: G4GeometryTolerance.cc:73

Here is the call graph for this function:

Here is the caller graph for this function:

G4Cons::~G4Cons ( )

Definition at line 151 of file G4Cons.cc.

152 {
153 }
G4Cons::G4Cons ( __void__ &  a)

Definition at line 137 of file G4Cons.cc.

138  : G4CSGSolid(a), kRadTolerance(0.), kAngTolerance(0.),
139  fRmin1(0.), fRmin2(0.), fRmax1(0.), fRmax2(0.), fDz(0.),
140  fSPhi(0.), fDPhi(0.), sinCPhi(0.), cosCPhi(0.), cosHDPhiOT(0.),
141  cosHDPhiIT(0.), sinSPhi(0.), cosSPhi(0.), sinEPhi(0.), cosEPhi(0.),
142  fPhiFullCone(false), halfCarTolerance(0.), halfRadTolerance(0.),
143  halfAngTolerance(0.)
144 {
145 }
a
std::vector< ExP01TrackerHit * > a
Definition: ExP01Classes.hh:33
G4CSGSolid::G4CSGSolid
G4CSGSolid(const G4String &pName)
Definition: G4CSGSolid.cc:49
G4Cons::G4Cons ( const G4Cons &  rhs)

Definition at line 159 of file G4Cons.cc.

160  : G4CSGSolid(rhs), kRadTolerance(rhs.kRadTolerance),
161  kAngTolerance(rhs.kAngTolerance), fRmin1(rhs.fRmin1), fRmin2(rhs.fRmin2),
162  fRmax1(rhs.fRmax1), fRmax2(rhs.fRmax2), fDz(rhs.fDz), fSPhi(rhs.fSPhi),
163  fDPhi(rhs.fDPhi), sinCPhi(rhs.sinCPhi), cosCPhi(rhs.cosCPhi),
164  cosHDPhiOT(rhs.cosHDPhiOT), cosHDPhiIT(rhs.cosHDPhiIT),
165  sinSPhi(rhs.sinSPhi), cosSPhi(rhs.cosSPhi), sinEPhi(rhs.sinEPhi),
166  cosEPhi(rhs.cosEPhi), fPhiFullCone(rhs.fPhiFullCone),
167  halfCarTolerance(rhs.halfCarTolerance),
168  halfRadTolerance(rhs.halfRadTolerance),
169  halfAngTolerance(rhs.halfAngTolerance)
170 {
171 }
G4CSGSolid::G4CSGSolid
G4CSGSolid(const G4String &pName)
Definition: G4CSGSolid.cc:49

Member Function Documentation

G4bool G4Cons::CalculateExtent ( const EAxis  pAxis,
const G4VoxelLimits &  pVoxelLimit,
const G4AffineTransform &  pTransform,
G4double &  pMin,
G4double &  pMax 
) const
virtual

Implements G4VSolid.

Definition at line 318 of file G4Cons.cc.

323 {
324  G4ThreeVector bmin, bmax;
325  G4bool exist;
326 
327  // Get bounding box
328  Extent(bmin,bmax);
329 
330  // Check bounding box
331  G4BoundingEnvelope bbox(bmin,bmax);
332 #ifdef G4BBOX_EXTENT
333  if (true) return bbox.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
334 #endif
335  if (bbox.BoundingBoxVsVoxelLimits(pAxis,pVoxelLimit,pTransform,pMin,pMax))
336  {
337  return exist = (pMin < pMax) ? true : false;
338  }
339 
340  // Get parameters of the solid
341  G4double rmin1 = GetInnerRadiusMinusZ();
342  G4double rmax1 = GetOuterRadiusMinusZ();
343  G4double rmin2 = GetInnerRadiusPlusZ();
344  G4double rmax2 = GetOuterRadiusPlusZ();
345  G4double dz = GetZHalfLength();
346  G4double dphi = GetDeltaPhiAngle();
347 
348  // Find bounding envelope and calculate extent
349  //
350  const G4int NSTEPS = 24; // number of steps for whole circle
351  G4double astep = twopi/NSTEPS; // max angle for one step
352  G4int ksteps = (dphi <= astep) ? 1 : (G4int)((dphi-deg)/astep) + 1;
353  G4double ang = dphi/ksteps;
354 
355  G4double sinHalf = std::sin(0.5*ang);
356  G4double cosHalf = std::cos(0.5*ang);
357  G4double sinStep = 2.*sinHalf*cosHalf;
358  G4double cosStep = 1. - 2.*sinHalf*sinHalf;
359  G4double rext1 = rmax1/cosHalf;
360  G4double rext2 = rmax2/cosHalf;
361 
362  // bounding envelope for full cone without hole consists of two polygons,
363  // in other cases it is a sequence of quadrilaterals
364  if (rmin1 == 0 && rmin2 == 0 && dphi == twopi)
365  {
366  G4double sinCur = sinHalf;
367  G4double cosCur = cosHalf;
368 
369  G4ThreeVectorList baseA(NSTEPS),baseB(NSTEPS);
370  for (G4int k=0; k<NSTEPS; ++k)
371  {
372  baseA[k].set(rext1*cosCur,rext1*sinCur,-dz);
373  baseB[k].set(rext2*cosCur,rext2*sinCur, dz);
374 
375  G4double sinTmp = sinCur;
376  sinCur = sinCur*cosStep + cosCur*sinStep;
377  cosCur = cosCur*cosStep - sinTmp*sinStep;
378  }
379  std::vector<const G4ThreeVectorList *> polygons(2);
380  polygons[0] = &baseA;
381  polygons[1] = &baseB;
382  G4BoundingEnvelope benv(bmin,bmax,polygons);
383  exist = benv.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
384  }
385  else
386  {
387  G4double sinStart = GetSinStartPhi();
388  G4double cosStart = GetCosStartPhi();
389  G4double sinEnd = GetSinEndPhi();
390  G4double cosEnd = GetCosEndPhi();
391  G4double sinCur = sinStart*cosHalf + cosStart*sinHalf;
392  G4double cosCur = cosStart*cosHalf - sinStart*sinHalf;
393 
394  // set quadrilaterals
395  G4ThreeVectorList pols[NSTEPS+2];
396  for (G4int k=0; k<ksteps+2; ++k) pols[k].resize(4);
397  pols[0][0].set(rmin2*cosStart,rmin2*sinStart, dz);
398  pols[0][1].set(rmin1*cosStart,rmin1*sinStart,-dz);
399  pols[0][2].set(rmax1*cosStart,rmax1*sinStart,-dz);
400  pols[0][3].set(rmax2*cosStart,rmax2*sinStart, dz);
401  for (G4int k=1; k<ksteps+1; ++k)
402  {
403  pols[k][0].set(rmin2*cosCur,rmin2*sinCur, dz);
404  pols[k][1].set(rmin1*cosCur,rmin1*sinCur,-dz);
405  pols[k][2].set(rext1*cosCur,rext1*sinCur,-dz);
406  pols[k][3].set(rext2*cosCur,rext2*sinCur, dz);
407 
408  G4double sinTmp = sinCur;
409  sinCur = sinCur*cosStep + cosCur*sinStep;
410  cosCur = cosCur*cosStep - sinTmp*sinStep;
411  }
412  pols[ksteps+1][0].set(rmin2*cosEnd,rmin2*sinEnd, dz);
413  pols[ksteps+1][1].set(rmin1*cosEnd,rmin1*sinEnd,-dz);
414  pols[ksteps+1][2].set(rmax1*cosEnd,rmax1*sinEnd,-dz);
415  pols[ksteps+1][3].set(rmax2*cosEnd,rmax2*sinEnd, dz);
416 
417  // set envelope and calculate extent
418  std::vector<const G4ThreeVectorList *> polygons;
419  polygons.resize(ksteps+2);
420  for (G4int k=0; k<ksteps+2; ++k) polygons[k] = &pols[k];
421  G4BoundingEnvelope benv(bmin,bmax,polygons);
422  exist = benv.CalculateExtent(pAxis,pVoxelLimit,pTransform,pMin,pMax);
423  }
424  return exist;
425 }
G4Cons::GetSinEndPhi
G4double GetSinEndPhi() const
G4Cons::GetOuterRadiusMinusZ
G4double GetOuterRadiusMinusZ() const
G4int
int G4int
Definition: G4Types.hh:78
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4Cons::GetSinStartPhi
G4double GetSinStartPhi() const
G4bool
bool G4bool
Definition: G4Types.hh:79
G4Cons::GetInnerRadiusPlusZ
G4double GetInnerRadiusPlusZ() const
G4ThreeVectorList
std::vector< G4ThreeVector > G4ThreeVectorList
Definition: G4BoundingEnvelope.hh:61
G4Cons::GetCosEndPhi
G4double GetCosEndPhi() const
G4Cons::Extent
void Extent(G4ThreeVector &pMin, G4ThreeVector &pMax) const
Definition: G4Cons.cc:276
G4Cons::GetCosStartPhi
G4double GetCosStartPhi() const
G4double
double G4double
Definition: G4Types.hh:76
G4Cons::GetInnerRadiusMinusZ
G4double GetInnerRadiusMinusZ() const
deg
static constexpr double deg
Definition: G4SIunits.hh:152
G4Cons::GetOuterRadiusPlusZ
G4double GetOuterRadiusPlusZ() const
G4Cons::GetZHalfLength
G4double GetZHalfLength() const
test1.astep
tuple astep
Definition: test1.py:13
G4Cons::GetDeltaPhiAngle
G4double GetDeltaPhiAngle() const

Here is the call graph for this function:

G4VSolid * G4Cons::Clone ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2105 of file G4Cons.cc.

2106 {
2107  return new G4Cons(*this);
2108 }
G4Cons::G4Cons
G4Cons(const G4String &pName, G4double pRmin1, G4double pRmax1, G4double pRmin2, G4double pRmax2, G4double pDz, G4double pSPhi, G4double pDPhi)
Definition: G4Cons.cc:87

Here is the call graph for this function:

void G4Cons::ComputeDimensions ( G4VPVParameterisation *  p,
const G4int  n,
const G4VPhysicalVolume *  pRep 
)
virtual

Reimplemented from G4VSolid.

Definition at line 265 of file G4Cons.cc.

268 {
269  p->ComputeDimensions(*this,n,pRep) ;
270 }
n
const G4int n
Definition: G4UrQMD1_3Interface.hh:144
G4VPVParameterisation::ComputeDimensions
virtual void ComputeDimensions(G4Box &, const G4int, const G4VPhysicalVolume *) const
Definition: G4VPVParameterisation.hh:95

Here is the call graph for this function:

G4Polyhedron * G4Cons::CreatePolyhedron ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2233 of file G4Cons.cc.

2234 {
2235  return new G4PolyhedronCons(fRmin1,fRmax1,fRmin2,fRmax2,fDz,fSPhi,fDPhi);
2236 }
void G4Cons::DescribeYourselfTo ( G4VGraphicsScene &  scene) const
virtual

Implements G4VSolid.

Definition at line 2228 of file G4Cons.cc.

2229 {
2230  scene.AddSolid (*this);
2231 }
G4VGraphicsScene::AddSolid
virtual void AddSolid(const G4Box &)=0

Here is the call graph for this function:

G4double G4Cons::DistanceToIn ( const G4ThreeVector &  p,
const G4ThreeVector &  v 
) const
virtual

Implements G4VSolid.

Definition at line 663 of file G4Cons.cc.

665 {
666  G4double snxt = kInfinity ; // snxt = default return value
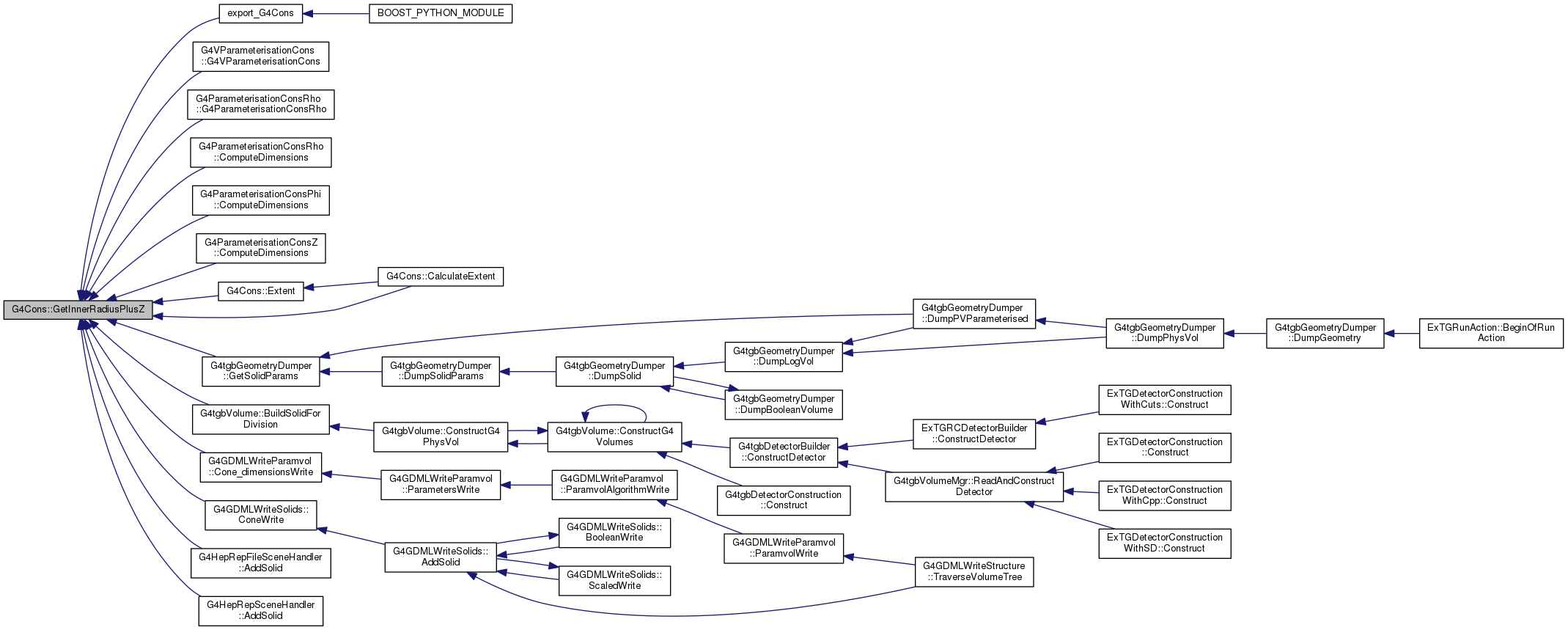
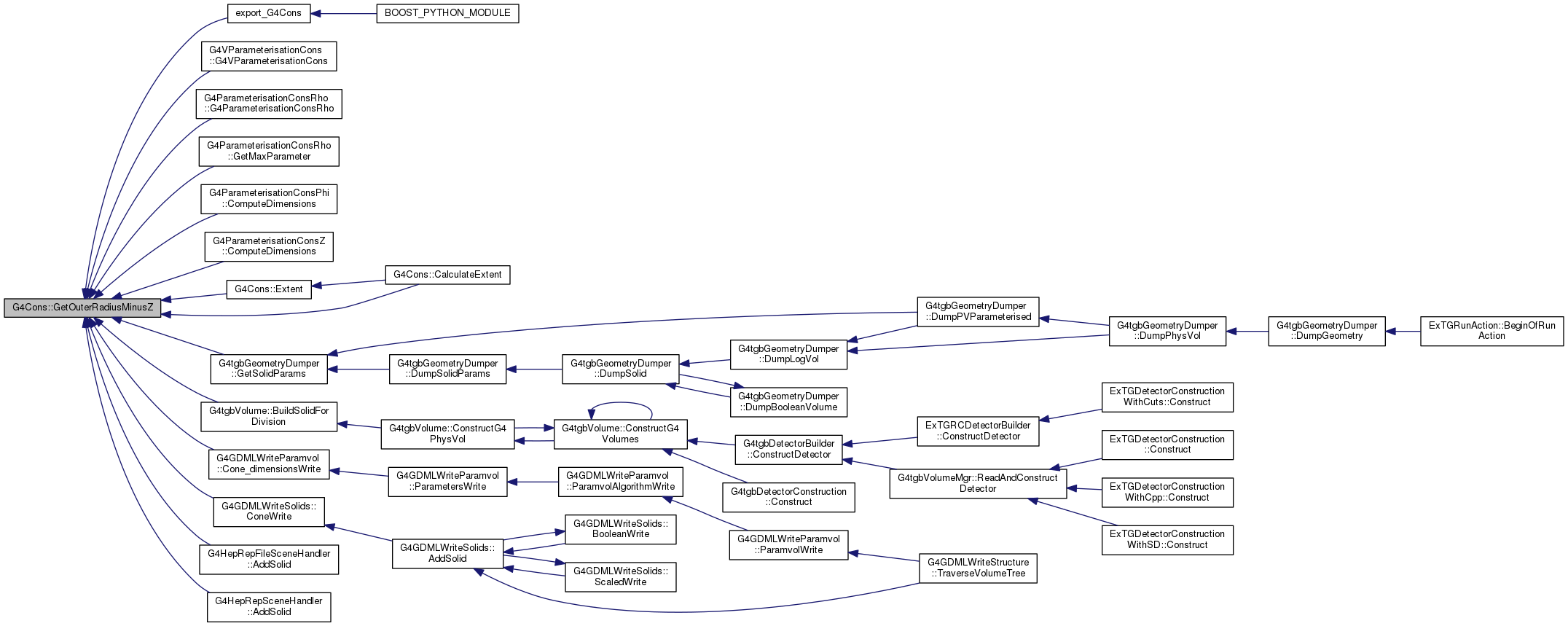
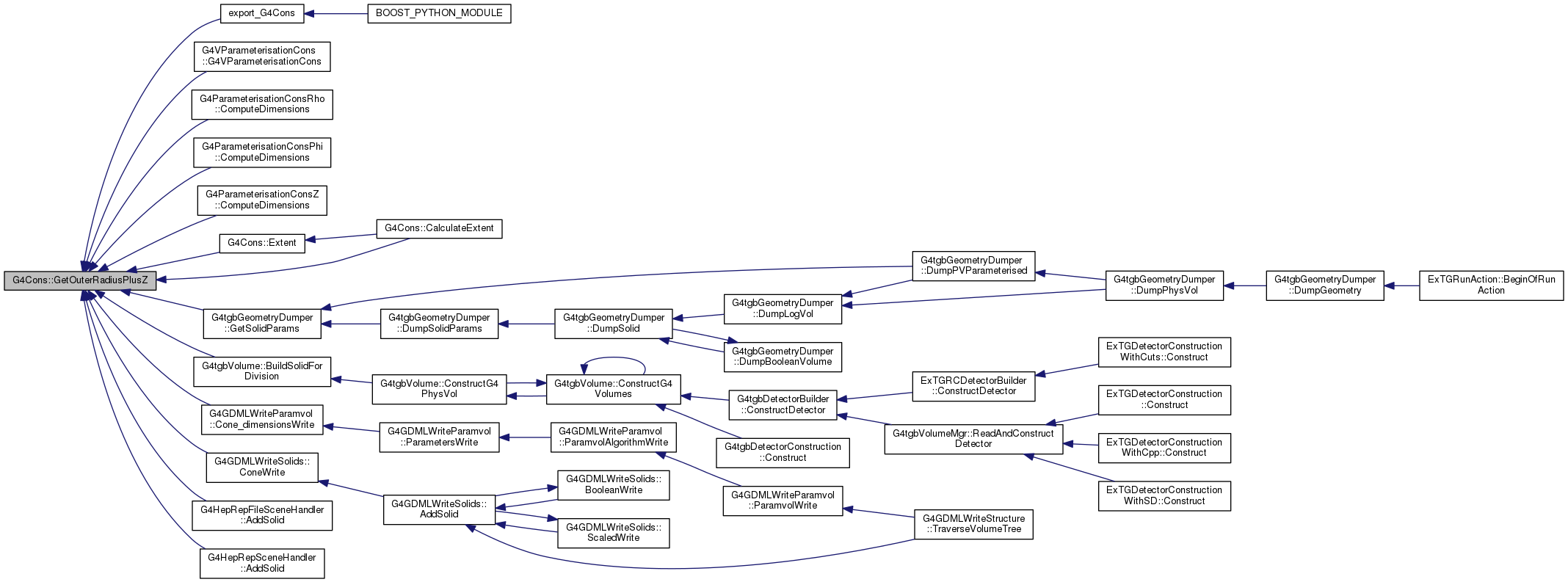
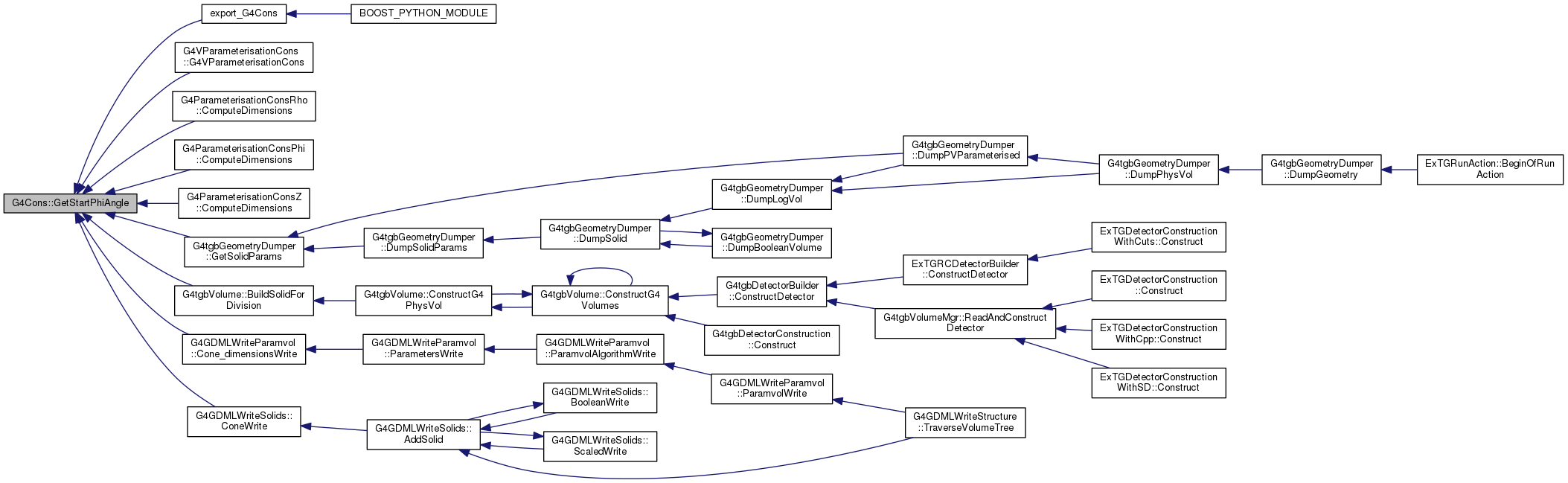
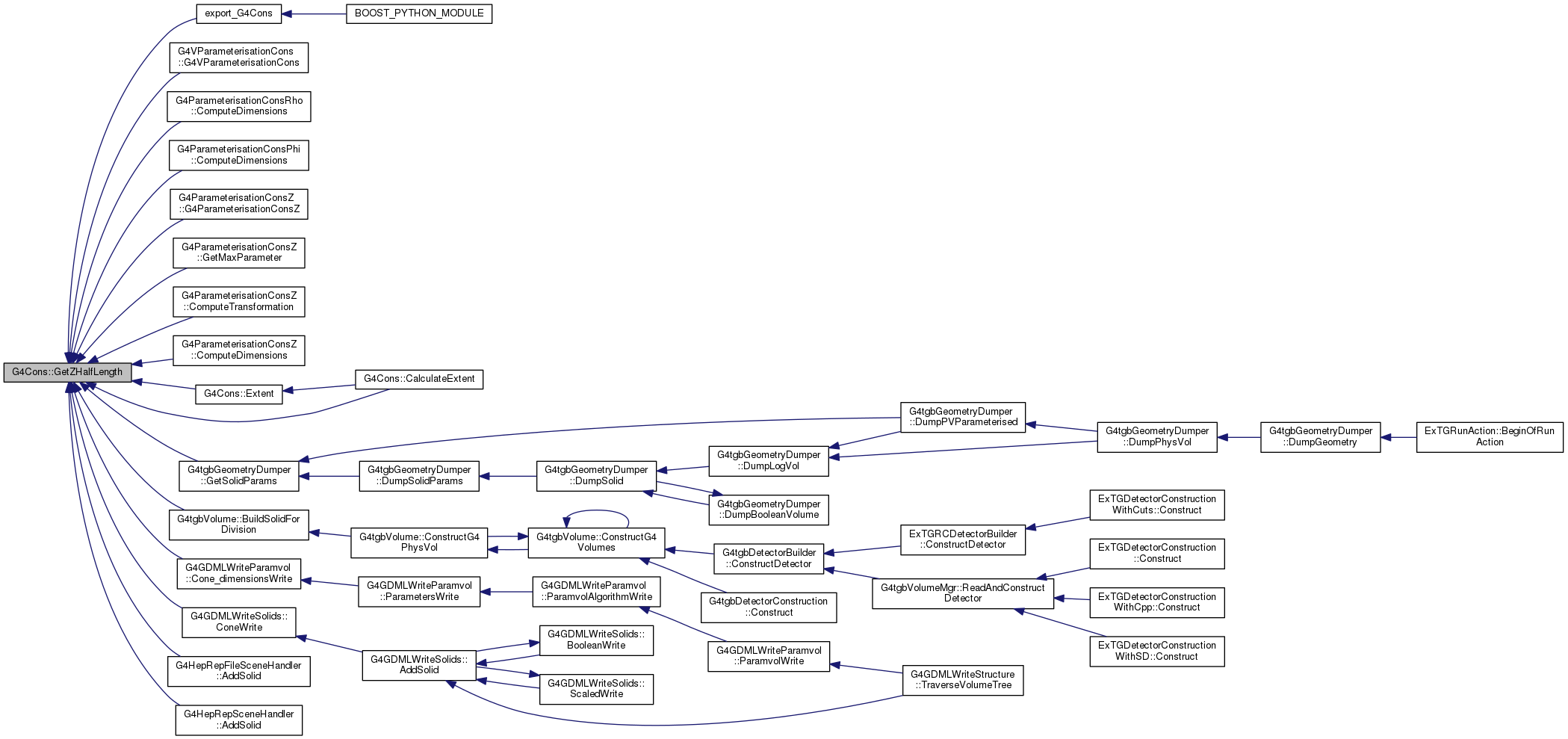
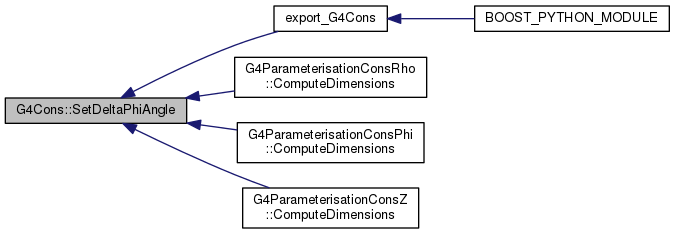
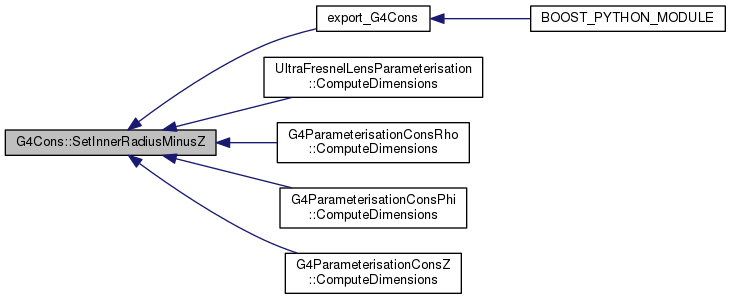
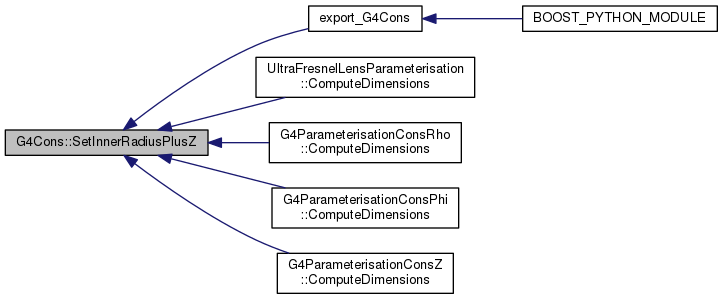
667  const G4double dRmax = 50*(fRmax1+fRmax2);// 100*(Rmax1+Rmax2)/2.
668 
669  G4double tanRMax,secRMax,rMaxAv,rMaxOAv ; // Data for cones
670  G4double tanRMin,secRMin,rMinAv,rMinOAv ;
671  G4double rout,rin ;
672 
673  G4double tolORMin,tolORMin2,tolIRMin,tolIRMin2 ; // `generous' radii squared
674  G4double tolORMax2,tolIRMax,tolIRMax2 ;
675  G4double tolODz,tolIDz ;
676 
677  G4double Dist,sd,xi,yi,zi,ri=0.,risec,rhoi2,cosPsi ; // Intersection point vars
678 
679  G4double t1,t2,t3,b,c,d ; // Quadratic solver variables
680  G4double nt1,nt2,nt3 ;
681  G4double Comp ;
682 
683  G4ThreeVector Normal;
684 
685  // Cone Precalcs
686 
687  tanRMin = (fRmin2 - fRmin1)*0.5/fDz ;
688  secRMin = std::sqrt(1.0 + tanRMin*tanRMin) ;
689  rMinAv = (fRmin1 + fRmin2)*0.5 ;
690 
691  if (rMinAv > halfRadTolerance)
692  {
693  rMinOAv = rMinAv - halfRadTolerance ;
694  }
695  else
696  {
697  rMinOAv = 0.0 ;
698  }
699  tanRMax = (fRmax2 - fRmax1)*0.5/fDz ;
700  secRMax = std::sqrt(1.0 + tanRMax*tanRMax) ;
701  rMaxAv = (fRmax1 + fRmax2)*0.5 ;
702  rMaxOAv = rMaxAv + halfRadTolerance ;
703 
704  // Intersection with z-surfaces
705 
706  tolIDz = fDz - halfCarTolerance ;
707  tolODz = fDz + halfCarTolerance ;
708 
709  if (std::fabs(p.z()) >= tolIDz)
710  {
711  if ( p.z()*v.z() < 0 ) // at +Z going in -Z or visa versa
712  {
713  sd = (std::fabs(p.z()) - fDz)/std::fabs(v.z()) ; // Z intersect distance
714 
715  if( sd < 0.0 ) { sd = 0.0; } // negative dist -> zero
716 
717  xi = p.x() + sd*v.x() ; // Intersection coords
718  yi = p.y() + sd*v.y() ;
719  rhoi2 = xi*xi + yi*yi ;
720 
721  // Check validity of intersection
722  // Calculate (outer) tolerant radi^2 at intersecion
723 
724  if (v.z() > 0)
725  {
726  tolORMin = fRmin1 - halfRadTolerance*secRMin ;
727  tolIRMin = fRmin1 + halfRadTolerance*secRMin ;
728  tolIRMax = fRmax1 - halfRadTolerance*secRMin ;
729  // tolORMax2 = (fRmax1 + halfRadTolerance*secRMax)*
730  // (fRmax1 + halfRadTolerance*secRMax) ;
731  }
732  else
733  {
734  tolORMin = fRmin2 - halfRadTolerance*secRMin ;
735  tolIRMin = fRmin2 + halfRadTolerance*secRMin ;
736  tolIRMax = fRmax2 - halfRadTolerance*secRMin ;
737  // tolORMax2 = (fRmax2 + halfRadTolerance*secRMax)*
738  // (fRmax2 + halfRadTolerance*secRMax) ;
739  }
740  if ( tolORMin > 0 )
741  {
742  // tolORMin2 = tolORMin*tolORMin ;
743  tolIRMin2 = tolIRMin*tolIRMin ;
744  }
745  else
746  {
747  // tolORMin2 = 0.0 ;
748  tolIRMin2 = 0.0 ;
749  }
750  if ( tolIRMax > 0 ) { tolIRMax2 = tolIRMax*tolIRMax; }
751  else { tolIRMax2 = 0.0; }
752 
753  if ( (tolIRMin2 <= rhoi2) && (rhoi2 <= tolIRMax2) )
754  {
755  if ( !fPhiFullCone && rhoi2 )
756  {
757  // Psi = angle made with central (average) phi of shape
758 
759  cosPsi = (xi*cosCPhi + yi*sinCPhi)/std::sqrt(rhoi2) ;
760 
761  if (cosPsi >= cosHDPhiIT) { return sd; }
762  }
763  else
764  {
765  return sd;
766  }
767  }
768  }
769  else // On/outside extent, and heading away -> cannot intersect
770  {
771  return snxt ;
772  }
773  }
774 
775 // ----> Can not intersect z surfaces
776 
777 
778 // Intersection with outer cone (possible return) and
779 // inner cone (must also check phi)
780 //
781 // Intersection point (xi,yi,zi) on line x=p.x+t*v.x etc.
782 //
783 // Intersects with x^2+y^2=(a*z+b)^2
784 //
785 // where a=tanRMax or tanRMin
786 // b=rMaxAv or rMinAv
787 //
788 // (vx^2+vy^2-(a*vz)^2)t^2+2t(pxvx+pyvy-a*vz(a*pz+b))+px^2+py^2-(a*pz+b)^2=0 ;
789 // t1 t2 t3
790 //
791 // \--------u-------/ \-----------v----------/ \---------w--------/
792 //
793 
794  t1 = 1.0 - v.z()*v.z() ;
795  t2 = p.x()*v.x() + p.y()*v.y() ;
796  t3 = p.x()*p.x() + p.y()*p.y() ;
797  rin = tanRMin*p.z() + rMinAv ;
798  rout = tanRMax*p.z() + rMaxAv ;
799 
800  // Outer Cone Intersection
801  // Must be outside/on outer cone for valid intersection
802 
803  nt1 = t1 - (tanRMax*v.z())*(tanRMax*v.z()) ;
804  nt2 = t2 - tanRMax*v.z()*rout ;
805  nt3 = t3 - rout*rout ;
806 
807  if (std::fabs(nt1) > kRadTolerance) // Equation quadratic => 2 roots
808  {
809  b = nt2/nt1;
810  c = nt3/nt1;
811  d = b*b-c ;
812  if ( (nt3 > rout*rout*kRadTolerance*kRadTolerance*secRMax*secRMax)
813  || (rout < 0) )
814  {
815  // If outside real cone (should be rho-rout>kRadTolerance*0.5
816  // NOT rho^2 etc) saves a std::sqrt() at expense of accuracy
817 
818  if (d >= 0)
819  {
820 
821  if ((rout < 0) && (nt3 <= 0))
822  {
823  // Inside `shadow cone' with -ve radius
824  // -> 2nd root could be on real cone
825 
826  if (b>0) { sd = c/(-b-std::sqrt(d)); }
827  else { sd = -b + std::sqrt(d); }
828  }
829  else
830  {
831  if ((b <= 0) && (c >= 0)) // both >=0, try smaller root
832  {
833  sd=c/(-b+std::sqrt(d));
834  }
835  else
836  {
837  if ( c <= 0 ) // second >=0
838  {
839  sd = -b + std::sqrt(d) ;
840  if((sd<0) & (sd>-halfRadTolerance)) sd=0;
841  }
842  else // both negative, travel away
843  {
844  return kInfinity ;
845  }
846  }
847  }
848  if ( sd >= 0 ) // If 'forwards'. Check z intersection
849  {
850  if ( sd>dRmax ) // Avoid rounding errors due to precision issues on
851  { // 64 bits systems. Split long distances and recompute
852  G4double fTerm = sd-std::fmod(sd,dRmax);
853  sd = fTerm + DistanceToIn(p+fTerm*v,v);
854  }
855  zi = p.z() + sd*v.z() ;
856 
857  if (std::fabs(zi) <= tolODz)
858  {
859  // Z ok. Check phi intersection if reqd
860 
861  if ( fPhiFullCone ) { return sd; }
862  else
863  {
864  xi = p.x() + sd*v.x() ;
865  yi = p.y() + sd*v.y() ;
866  ri = rMaxAv + zi*tanRMax ;
867  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri ;
868 
869  if ( cosPsi >= cosHDPhiIT ) { return sd; }
870  }
871  }
872  } // end if (sd>0)
873  }
874  }
875  else
876  {
877  // Inside outer cone
878  // check not inside, and heading through G4Cons (-> 0 to in)
879 
880  if ( ( t3 > (rin + halfRadTolerance*secRMin)*
881  (rin + halfRadTolerance*secRMin) )
882  && (nt2 < 0) && (d >= 0) && (std::fabs(p.z()) <= tolIDz) )
883  {
884  // Inside cones, delta r -ve, inside z extent
885  // Point is on the Surface => check Direction using Normal.dot(v)
886 
887  xi = p.x() ;
888  yi = p.y() ;
889  risec = std::sqrt(xi*xi + yi*yi)*secRMax ;
890  Normal = G4ThreeVector(xi/risec,yi/risec,-tanRMax/secRMax) ;
891  if ( !fPhiFullCone )
892  {
893  cosPsi = (p.x()*cosCPhi + p.y()*sinCPhi)/std::sqrt(t3) ;
894  if ( cosPsi >= cosHDPhiIT )
895  {
896  if ( Normal.dot(v) <= 0 ) { return 0.0; }
897  }
898  }
899  else
900  {
901  if ( Normal.dot(v) <= 0 ) { return 0.0; }
902  }
903  }
904  }
905  }
906  else // Single root case
907  {
908  if ( std::fabs(nt2) > kRadTolerance )
909  {
910  sd = -0.5*nt3/nt2 ;
911 
912  if ( sd < 0 ) { return kInfinity; } // travel away
913  else // sd >= 0, If 'forwards'. Check z intersection
914  {
915  zi = p.z() + sd*v.z() ;
916 
917  if ((std::fabs(zi) <= tolODz) && (nt2 < 0))
918  {
919  // Z ok. Check phi intersection if reqd
920 
921  if ( fPhiFullCone ) { return sd; }
922  else
923  {
924  xi = p.x() + sd*v.x() ;
925  yi = p.y() + sd*v.y() ;
926  ri = rMaxAv + zi*tanRMax ;
927  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri ;
928 
929  if (cosPsi >= cosHDPhiIT) { return sd; }
930  }
931  }
932  }
933  }
934  else // travel || cone surface from its origin
935  {
936  sd = kInfinity ;
937  }
938  }
939 
940  // Inner Cone Intersection
941  // o Space is divided into 3 areas:
942  // 1) Radius greater than real inner cone & imaginary cone & outside
943  // tolerance
944  // 2) Radius less than inner or imaginary cone & outside tolarance
945  // 3) Within tolerance of real or imaginary cones
946  // - Extra checks needed for 3's intersections
947  // => lots of duplicated code
948 
949  if (rMinAv)
950  {
951  nt1 = t1 - (tanRMin*v.z())*(tanRMin*v.z()) ;
952  nt2 = t2 - tanRMin*v.z()*rin ;
953  nt3 = t3 - rin*rin ;
954 
955  if ( nt1 )
956  {
957  if ( nt3 > rin*kRadTolerance*secRMin )
958  {
959  // At radius greater than real & imaginary cones
960  // -> 2nd root, with zi check
961 
962  b = nt2/nt1 ;
963  c = nt3/nt1 ;
964  d = b*b-c ;
965  if (d >= 0) // > 0
966  {
967  if(b>0){sd = c/( -b-std::sqrt(d));}
968  else {sd = -b + std::sqrt(d) ;}
969 
970  if ( sd >= 0 ) // > 0
971  {
972  if ( sd>dRmax ) // Avoid rounding errors due to precision issues on
973  { // 64 bits systems. Split long distance and recompute
974  G4double fTerm = sd-std::fmod(sd,dRmax);
975  sd = fTerm + DistanceToIn(p+fTerm*v,v);
976  }
977  zi = p.z() + sd*v.z() ;
978 
979  if ( std::fabs(zi) <= tolODz )
980  {
981  if ( !fPhiFullCone )
982  {
983  xi = p.x() + sd*v.x() ;
984  yi = p.y() + sd*v.y() ;
985  ri = rMinAv + zi*tanRMin ;
986  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri ;
987 
988  if (cosPsi >= cosHDPhiIT)
989  {
990  if ( sd > halfRadTolerance ) { snxt=sd; }
991  else
992  {
993  // Calculate a normal vector in order to check Direction
994 
995  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
996  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin);
997  if ( Normal.dot(v) <= 0 ) { snxt = sd; }
998  }
999  }
1000  }
1001  else
1002  {
1003  if ( sd > halfRadTolerance ) { return sd; }
1004  else
1005  {
1006  // Calculate a normal vector in order to check Direction
1007 
1008  xi = p.x() + sd*v.x() ;
1009  yi = p.y() + sd*v.y() ;
1010  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
1011  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin) ;
1012  if ( Normal.dot(v) <= 0 ) { return sd; }
1013  }
1014  }
1015  }
1016  }
1017  }
1018  }
1019  else if ( nt3 < -rin*kRadTolerance*secRMin )
1020  {
1021  // Within radius of inner cone (real or imaginary)
1022  // -> Try 2nd root, with checking intersection is with real cone
1023  // -> If check fails, try 1st root, also checking intersection is
1024  // on real cone
1025 
1026  b = nt2/nt1 ;
1027  c = nt3/nt1 ;
1028  d = b*b - c ;
1029 
1030  if ( d >= 0 ) // > 0
1031  {
1032  if (b>0) { sd = c/(-b-std::sqrt(d)); }
1033  else { sd = -b + std::sqrt(d); }
1034  zi = p.z() + sd*v.z() ;
1035  ri = rMinAv + zi*tanRMin ;
1036 
1037  if ( ri > 0 )
1038  {
1039  if ( (sd >= 0) && (std::fabs(zi) <= tolODz) ) // sd > 0
1040  {
1041  if ( sd>dRmax ) // Avoid rounding errors due to precision issues
1042  { // seen on 64 bits systems. Split and recompute
1043  G4double fTerm = sd-std::fmod(sd,dRmax);
1044  sd = fTerm + DistanceToIn(p+fTerm*v,v);
1045  }
1046  if ( !fPhiFullCone )
1047  {
1048  xi = p.x() + sd*v.x() ;
1049  yi = p.y() + sd*v.y() ;
1050  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri ;
1051 
1052  if (cosPsi >= cosHDPhiOT)
1053  {
1054  if ( sd > halfRadTolerance ) { snxt=sd; }
1055  else
1056  {
1057  // Calculate a normal vector in order to check Direction
1058 
1059  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
1060  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin);
1061  if ( Normal.dot(v) <= 0 ) { snxt = sd; }
1062  }
1063  }
1064  }
1065  else
1066  {
1067  if( sd > halfRadTolerance ) { return sd; }
1068  else
1069  {
1070  // Calculate a normal vector in order to check Direction
1071 
1072  xi = p.x() + sd*v.x() ;
1073  yi = p.y() + sd*v.y() ;
1074  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
1075  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin) ;
1076  if ( Normal.dot(v) <= 0 ) { return sd; }
1077  }
1078  }
1079  }
1080  }
1081  else
1082  {
1083  if (b>0) { sd = -b - std::sqrt(d); }
1084  else { sd = c/(-b+std::sqrt(d)); }
1085  zi = p.z() + sd*v.z() ;
1086  ri = rMinAv + zi*tanRMin ;
1087 
1088  if ( (sd >= 0) && (ri > 0) && (std::fabs(zi) <= tolODz) ) // sd>0
1089  {
1090  if ( sd>dRmax ) // Avoid rounding errors due to precision issues
1091  { // seen on 64 bits systems. Split and recompute
1092  G4double fTerm = sd-std::fmod(sd,dRmax);
1093  sd = fTerm + DistanceToIn(p+fTerm*v,v);
1094  }
1095  if ( !fPhiFullCone )
1096  {
1097  xi = p.x() + sd*v.x() ;
1098  yi = p.y() + sd*v.y() ;
1099  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri ;
1100 
1101  if (cosPsi >= cosHDPhiIT)
1102  {
1103  if ( sd > halfRadTolerance ) { snxt=sd; }
1104  else
1105  {
1106  // Calculate a normal vector in order to check Direction
1107 
1108  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
1109  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin);
1110  if ( Normal.dot(v) <= 0 ) { snxt = sd; }
1111  }
1112  }
1113  }
1114  else
1115  {
1116  if ( sd > halfRadTolerance ) { return sd; }
1117  else
1118  {
1119  // Calculate a normal vector in order to check Direction
1120 
1121  xi = p.x() + sd*v.x() ;
1122  yi = p.y() + sd*v.y() ;
1123  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
1124  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin) ;
1125  if ( Normal.dot(v) <= 0 ) { return sd; }
1126  }
1127  }
1128  }
1129  }
1130  }
1131  }
1132  else
1133  {
1134  // Within kRadTol*0.5 of inner cone (real OR imaginary)
1135  // ----> Check not travelling through (=>0 to in)
1136  // ----> if not:
1137  // -2nd root with validity check
1138 
1139  if ( std::fabs(p.z()) <= tolODz )
1140  {
1141  if ( nt2 > 0 )
1142  {
1143  // Inside inner real cone, heading outwards, inside z range
1144 
1145  if ( !fPhiFullCone )
1146  {
1147  cosPsi = (p.x()*cosCPhi + p.y()*sinCPhi)/std::sqrt(t3) ;
1148 
1149  if (cosPsi >= cosHDPhiIT) { return 0.0; }
1150  }
1151  else { return 0.0; }
1152  }
1153  else
1154  {
1155  // Within z extent, but not travelling through
1156  // -> 2nd root or kInfinity if 1st root on imaginary cone
1157 
1158  b = nt2/nt1 ;
1159  c = nt3/nt1 ;
1160  d = b*b - c ;
1161 
1162  if ( d >= 0 ) // > 0
1163  {
1164  if (b>0) { sd = -b - std::sqrt(d); }
1165  else { sd = c/(-b+std::sqrt(d)); }
1166  zi = p.z() + sd*v.z() ;
1167  ri = rMinAv + zi*tanRMin ;
1168 
1169  if ( ri > 0 ) // 2nd root
1170  {
1171  if (b>0) { sd = c/(-b-std::sqrt(d)); }
1172  else { sd = -b + std::sqrt(d); }
1173 
1174  zi = p.z() + sd*v.z() ;
1175 
1176  if ( (sd >= 0) && (std::fabs(zi) <= tolODz) ) // sd>0
1177  {
1178  if ( sd>dRmax ) // Avoid rounding errors due to precision issue
1179  { // seen on 64 bits systems. Split and recompute
1180  G4double fTerm = sd-std::fmod(sd,dRmax);
1181  sd = fTerm + DistanceToIn(p+fTerm*v,v);
1182  }
1183  if ( !fPhiFullCone )
1184  {
1185  xi = p.x() + sd*v.x() ;
1186  yi = p.y() + sd*v.y() ;
1187  ri = rMinAv + zi*tanRMin ;
1188  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri ;
1189 
1190  if ( cosPsi >= cosHDPhiIT ) { snxt = sd; }
1191  }
1192  else { return sd; }
1193  }
1194  }
1195  else { return kInfinity; }
1196  }
1197  }
1198  }
1199  else // 2nd root
1200  {
1201  b = nt2/nt1 ;
1202  c = nt3/nt1 ;
1203  d = b*b - c ;
1204 
1205  if ( d > 0 )
1206  {
1207  if (b>0) { sd = c/(-b-std::sqrt(d)); }
1208  else { sd = -b + std::sqrt(d) ; }
1209  zi = p.z() + sd*v.z() ;
1210 
1211  if ( (sd >= 0) && (std::fabs(zi) <= tolODz) ) // sd>0
1212  {
1213  if ( sd>dRmax ) // Avoid rounding errors due to precision issues
1214  { // seen on 64 bits systems. Split and recompute
1215  G4double fTerm = sd-std::fmod(sd,dRmax);
1216  sd = fTerm + DistanceToIn(p+fTerm*v,v);
1217  }
1218  if ( !fPhiFullCone )
1219  {
1220  xi = p.x() + sd*v.x();
1221  yi = p.y() + sd*v.y();
1222  ri = rMinAv + zi*tanRMin ;
1223  cosPsi = (xi*cosCPhi + yi*sinCPhi)/ri;
1224 
1225  if (cosPsi >= cosHDPhiIT) { snxt = sd; }
1226  }
1227  else { return sd; }
1228  }
1229  }
1230  }
1231  }
1232  }
1233  }
1234 
1235  // Phi segment intersection
1236  //
1237  // o Tolerant of points inside phi planes by up to kCarTolerance*0.5
1238  //
1239  // o NOTE: Large duplication of code between sphi & ephi checks
1240  // -> only diffs: sphi -> ephi, Comp -> -Comp and half-plane
1241  // intersection check <=0 -> >=0
1242  // -> Should use some form of loop Construct
1243 
1244  if ( !fPhiFullCone )
1245  {
1246  // First phi surface (starting phi)
1247 
1248  Comp = v.x()*sinSPhi - v.y()*cosSPhi ;
1249 
1250  if ( Comp < 0 ) // Component in outwards normal dirn
1251  {
1252  Dist = (p.y()*cosSPhi - p.x()*sinSPhi) ;
1253 
1254  if (Dist < halfCarTolerance)
1255  {
1256  sd = Dist/Comp ;
1257 
1258  if ( sd < snxt )
1259  {
1260  if ( sd < 0 ) { sd = 0.0; }
1261 
1262  zi = p.z() + sd*v.z() ;
1263 
1264  if ( std::fabs(zi) <= tolODz )
1265  {
1266  xi = p.x() + sd*v.x() ;
1267  yi = p.y() + sd*v.y() ;
1268  rhoi2 = xi*xi + yi*yi ;
1269  tolORMin2 = (rMinOAv + zi*tanRMin)*(rMinOAv + zi*tanRMin) ;
1270  tolORMax2 = (rMaxOAv + zi*tanRMax)*(rMaxOAv + zi*tanRMax) ;
1271 
1272  if ( (rhoi2 >= tolORMin2) && (rhoi2 <= tolORMax2) )
1273  {
1274  // z and r intersections good - check intersecting with
1275  // correct half-plane
1276 
1277  if ((yi*cosCPhi - xi*sinCPhi) <= 0 ) { snxt = sd; }
1278  }
1279  }
1280  }
1281  }
1282  }
1283 
1284  // Second phi surface (Ending phi)
1285 
1286  Comp = -(v.x()*sinEPhi - v.y()*cosEPhi) ;
1287 
1288  if ( Comp < 0 ) // Component in outwards normal dirn
1289  {
1290  Dist = -(p.y()*cosEPhi - p.x()*sinEPhi) ;
1291  if (Dist < halfCarTolerance)
1292  {
1293  sd = Dist/Comp ;
1294 
1295  if ( sd < snxt )
1296  {
1297  if ( sd < 0 ) { sd = 0.0; }
1298 
1299  zi = p.z() + sd*v.z() ;
1300 
1301  if (std::fabs(zi) <= tolODz)
1302  {
1303  xi = p.x() + sd*v.x() ;
1304  yi = p.y() + sd*v.y() ;
1305  rhoi2 = xi*xi + yi*yi ;
1306  tolORMin2 = (rMinOAv + zi*tanRMin)*(rMinOAv + zi*tanRMin) ;
1307  tolORMax2 = (rMaxOAv + zi*tanRMax)*(rMaxOAv + zi*tanRMax) ;
1308 
1309  if ( (rhoi2 >= tolORMin2) && (rhoi2 <= tolORMax2) )
1310  {
1311  // z and r intersections good - check intersecting with
1312  // correct half-plane
1313 
1314  if ( (yi*cosCPhi - xi*sinCPhi) >= 0.0 ) { snxt = sd; }
1315  }
1316  }
1317  }
1318  }
1319  }
1320  }
1321  if (snxt < halfCarTolerance) { snxt = 0.; }
1322 
1323  return snxt ;
1324 }
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
CLHEP::Hep3Vector::x
double x() const
CLHEP::Hep3Vector::dot
double dot(const Hep3Vector &) const
G4Cons::DistanceToIn
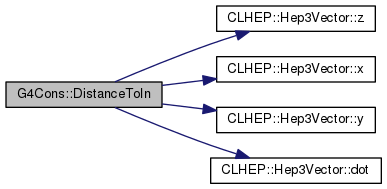
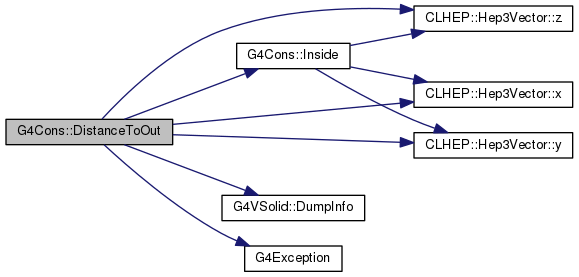
G4double DistanceToIn(const G4ThreeVector &p, const G4ThreeVector &v) const
Definition: G4Cons.cc:663
CLHEP::Hep3Vector::z
double z() const
test.b
tuple b
Definition: test.py:12
plottest35.t1
tuple t1
Definition: plottest35.py:33
CLHEP::Hep3Vector::y
double y() const
G4double
double G4double
Definition: G4Types.hh:76
test.c
tuple c
Definition: test.py:13

Here is the call graph for this function:

G4double G4Cons::DistanceToIn ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 1333 of file G4Cons.cc.

1334 {
1335  G4double safe=0.0, rho, safeR1, safeR2, safeZ, safePhi, cosPsi ;
1336  G4double tanRMin, secRMin, pRMin ;
1337  G4double tanRMax, secRMax, pRMax ;
1338 
1339  rho = std::sqrt(p.x()*p.x() + p.y()*p.y()) ;
1340  safeZ = std::fabs(p.z()) - fDz ;
1341 
1342  if ( fRmin1 || fRmin2 )
1343  {
1344  tanRMin = (fRmin2 - fRmin1)*0.5/fDz ;
1345  secRMin = std::sqrt(1.0 + tanRMin*tanRMin) ;
1346  pRMin = tanRMin*p.z() + (fRmin1 + fRmin2)*0.5 ;
1347  safeR1 = (pRMin - rho)/secRMin ;
1348 
1349  tanRMax = (fRmax2 - fRmax1)*0.5/fDz ;
1350  secRMax = std::sqrt(1.0 + tanRMax*tanRMax) ;
1351  pRMax = tanRMax*p.z() + (fRmax1 + fRmax2)*0.5 ;
1352  safeR2 = (rho - pRMax)/secRMax ;
1353 
1354  if ( safeR1 > safeR2) { safe = safeR1; }
1355  else { safe = safeR2; }
1356  }
1357  else
1358  {
1359  tanRMax = (fRmax2 - fRmax1)*0.5/fDz ;
1360  secRMax = std::sqrt(1.0 + tanRMax*tanRMax) ;
1361  pRMax = tanRMax*p.z() + (fRmax1 + fRmax2)*0.5 ;
1362  safe = (rho - pRMax)/secRMax ;
1363  }
1364  if ( safeZ > safe ) { safe = safeZ; }
1365 
1366  if ( !fPhiFullCone && rho )
1367  {
1368  // Psi=angle from central phi to point
1369 
1370  cosPsi = (p.x()*cosCPhi + p.y()*sinCPhi)/rho ;
1371 
1372  if ( cosPsi < std::cos(fDPhi*0.5) ) // Point lies outside phi range
1373  {
1374  if ( (p.y()*cosCPhi - p.x()*sinCPhi) <= 0.0 )
1375  {
1376  safePhi = std::fabs(p.x()*std::sin(fSPhi)-p.y()*std::cos(fSPhi));
1377  }
1378  else
1379  {
1380  safePhi = std::fabs(p.x()*sinEPhi-p.y()*cosEPhi);
1381  }
1382  if ( safePhi > safe ) { safe = safePhi; }
1383  }
1384  }
1385  if ( safe < 0.0 ) { safe = 0.0; }
1386 
1387  return safe ;
1388 }
CLHEP::Hep3Vector::x
double x() const
CLHEP::Hep3Vector::z
double z() const
CLHEP::Hep3Vector::y
double y() const
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

G4double G4Cons::DistanceToOut ( const G4ThreeVector &  p,
const G4ThreeVector &  v,
const G4bool  calcNorm = G4bool(false),
G4bool *  validNorm = 0,
G4ThreeVector *  n = 0 
) const
virtual

Implements G4VSolid.

Definition at line 1395 of file G4Cons.cc.

1400 {
1401  ESide side = kNull, sider = kNull, sidephi = kNull;
1402 
1403  G4double snxt,srd,sphi,pdist ;
1404 
1405  G4double tanRMax, secRMax, rMaxAv ; // Data for outer cone
1406  G4double tanRMin, secRMin, rMinAv ; // Data for inner cone
1407 
1408  G4double t1, t2, t3, rout, rin, nt1, nt2, nt3 ;
1409  G4double b, c, d, sr2, sr3 ;
1410 
1411  // Vars for intersection within tolerance
1412 
1413  ESide sidetol = kNull ;
1414  G4double slentol = kInfinity ;
1415 
1416  // Vars for phi intersection:
1417 
1418  G4double pDistS, compS, pDistE, compE, sphi2, xi, yi, risec, vphi ;
1419  G4double zi, ri, deltaRoi2 ;
1420 
1421  // Z plane intersection
1422 
1423  if ( v.z() > 0.0 )
1424  {
1425  pdist = fDz - p.z() ;
1426 
1427  if (pdist > halfCarTolerance)
1428  {
1429  snxt = pdist/v.z() ;
1430  side = kPZ ;
1431  }
1432  else
1433  {
1434  if (calcNorm)
1435  {
1436  *n = G4ThreeVector(0,0,1) ;
1437  *validNorm = true ;
1438  }
1439  return snxt = 0.0;
1440  }
1441  }
1442  else if ( v.z() < 0.0 )
1443  {
1444  pdist = fDz + p.z() ;
1445 
1446  if ( pdist > halfCarTolerance)
1447  {
1448  snxt = -pdist/v.z() ;
1449  side = kMZ ;
1450  }
1451  else
1452  {
1453  if ( calcNorm )
1454  {
1455  *n = G4ThreeVector(0,0,-1) ;
1456  *validNorm = true ;
1457  }
1458  return snxt = 0.0 ;
1459  }
1460  }
1461  else // Travel perpendicular to z axis
1462  {
1463  snxt = kInfinity ;
1464  side = kNull ;
1465  }
1466 
1467  // Radial Intersections
1468  //
1469  // Intersection with outer cone (possible return) and
1470  // inner cone (must also check phi)
1471  //
1472  // Intersection point (xi,yi,zi) on line x=p.x+t*v.x etc.
1473  //
1474  // Intersects with x^2+y^2=(a*z+b)^2
1475  //
1476  // where a=tanRMax or tanRMin
1477  // b=rMaxAv or rMinAv
1478  //
1479  // (vx^2+vy^2-(a*vz)^2)t^2+2t(pxvx+pyvy-a*vz(a*pz+b))+px^2+py^2-(a*pz+b)^2=0 ;
1480  // t1 t2 t3
1481  //
1482  // \--------u-------/ \-----------v----------/ \---------w--------/
1483 
1484  tanRMax = (fRmax2 - fRmax1)*0.5/fDz ;
1485  secRMax = std::sqrt(1.0 + tanRMax*tanRMax) ;
1486  rMaxAv = (fRmax1 + fRmax2)*0.5 ;
1487 
1488 
1489  t1 = 1.0 - v.z()*v.z() ; // since v normalised
1490  t2 = p.x()*v.x() + p.y()*v.y() ;
1491  t3 = p.x()*p.x() + p.y()*p.y() ;
1492  rout = tanRMax*p.z() + rMaxAv ;
1493 
1494  nt1 = t1 - (tanRMax*v.z())*(tanRMax*v.z()) ;
1495  nt2 = t2 - tanRMax*v.z()*rout ;
1496  nt3 = t3 - rout*rout ;
1497 
1498  if (v.z() > 0.0)
1499  {
1500  deltaRoi2 = snxt*snxt*t1 + 2*snxt*t2 + t3
1501  - fRmax2*(fRmax2 + kRadTolerance*secRMax);
1502  }
1503  else if ( v.z() < 0.0 )
1504  {
1505  deltaRoi2 = snxt*snxt*t1 + 2*snxt*t2 + t3
1506  - fRmax1*(fRmax1 + kRadTolerance*secRMax);
1507  }
1508  else
1509  {
1510  deltaRoi2 = 1.0;
1511  }
1512 
1513  if ( nt1 && (deltaRoi2 > 0.0) )
1514  {
1515  // Equation quadratic => 2 roots : second root must be leaving
1516 
1517  b = nt2/nt1 ;
1518  c = nt3/nt1 ;
1519  d = b*b - c ;
1520 
1521  if ( d >= 0 )
1522  {
1523  // Check if on outer cone & heading outwards
1524  // NOTE: Should use rho-rout>-kRadTolerance*0.5
1525 
1526  if (nt3 > -halfRadTolerance && nt2 >= 0 )
1527  {
1528  if (calcNorm)
1529  {
1530  risec = std::sqrt(t3)*secRMax ;
1531  *validNorm = true ;
1532  *n = G4ThreeVector(p.x()/risec,p.y()/risec,-tanRMax/secRMax);
1533  }
1534  return snxt=0 ;
1535  }
1536  else
1537  {
1538  sider = kRMax ;
1539  if (b>0) { srd = -b - std::sqrt(d); }
1540  else { srd = c/(-b+std::sqrt(d)) ; }
1541 
1542  zi = p.z() + srd*v.z() ;
1543  ri = tanRMax*zi + rMaxAv ;
1544 
1545  if ((ri >= 0) && (-halfRadTolerance <= srd) && (srd <= halfRadTolerance))
1546  {
1547  // An intersection within the tolerance
1548  // we will Store it in case it is good -
1549  //
1550  slentol = srd ;
1551  sidetol = kRMax ;
1552  }
1553  if ( (ri < 0) || (srd < halfRadTolerance) )
1554  {
1555  // Safety: if both roots -ve ensure that srd cannot `win'
1556  // distance to out
1557 
1558  if (b>0) { sr2 = c/(-b-std::sqrt(d)); }
1559  else { sr2 = -b + std::sqrt(d); }
1560  zi = p.z() + sr2*v.z() ;
1561  ri = tanRMax*zi + rMaxAv ;
1562 
1563  if ((ri >= 0) && (sr2 > halfRadTolerance))
1564  {
1565  srd = sr2;
1566  }
1567  else
1568  {
1569  srd = kInfinity ;
1570 
1571  if( (-halfRadTolerance <= sr2) && ( sr2 <= halfRadTolerance) )
1572  {
1573  // An intersection within the tolerance.
1574  // Storing it in case it is good.
1575 
1576  slentol = sr2 ;
1577  sidetol = kRMax ;
1578  }
1579  }
1580  }
1581  }
1582  }
1583  else
1584  {
1585  // No intersection with outer cone & not parallel
1586  // -> already outside, no intersection
1587 
1588  if ( calcNorm )
1589  {
1590  risec = std::sqrt(t3)*secRMax;
1591  *validNorm = true;
1592  *n = G4ThreeVector(p.x()/risec,p.y()/risec,-tanRMax/secRMax);
1593  }
1594  return snxt = 0.0 ;
1595  }
1596  }
1597  else if ( nt2 && (deltaRoi2 > 0.0) )
1598  {
1599  // Linear case (only one intersection) => point outside outer cone
1600 
1601  if ( calcNorm )
1602  {
1603  risec = std::sqrt(t3)*secRMax;
1604  *validNorm = true;
1605  *n = G4ThreeVector(p.x()/risec,p.y()/risec,-tanRMax/secRMax);
1606  }
1607  return snxt = 0.0 ;
1608  }
1609  else
1610  {
1611  // No intersection -> parallel to outer cone
1612  // => Z or inner cone intersection
1613 
1614  srd = kInfinity ;
1615  }
1616 
1617  // Check possible intersection within tolerance
1618 
1619  if ( slentol <= halfCarTolerance )
1620  {
1621  // An intersection within the tolerance was found.
1622  // We must accept it only if the momentum points outwards.
1623  //
1624  // G4ThreeVector ptTol ; // The point of the intersection
1625  // ptTol= p + slentol*v ;
1626  // ri=tanRMax*zi+rMaxAv ;
1627  //
1628  // Calculate a normal vector, as below
1629 
1630  xi = p.x() + slentol*v.x();
1631  yi = p.y() + slentol*v.y();
1632  risec = std::sqrt(xi*xi + yi*yi)*secRMax;
1633  G4ThreeVector Normal = G4ThreeVector(xi/risec,yi/risec,-tanRMax/secRMax);
1634 
1635  if ( Normal.dot(v) > 0 ) // We will leave the Cone immediatelly
1636  {
1637  if ( calcNorm )
1638  {
1639  *n = Normal.unit() ;
1640  *validNorm = true ;
1641  }
1642  return snxt = 0.0 ;
1643  }
1644  else // On the surface, but not heading out so we ignore this intersection
1645  { // (as it is within tolerance).
1646  slentol = kInfinity ;
1647  }
1648  }
1649 
1650  // Inner Cone intersection
1651 
1652  if ( fRmin1 || fRmin2 )
1653  {
1654  tanRMin = (fRmin2 - fRmin1)*0.5/fDz ;
1655  nt1 = t1 - (tanRMin*v.z())*(tanRMin*v.z()) ;
1656 
1657  if ( nt1 )
1658  {
1659  secRMin = std::sqrt(1.0 + tanRMin*tanRMin) ;
1660  rMinAv = (fRmin1 + fRmin2)*0.5 ;
1661  rin = tanRMin*p.z() + rMinAv ;
1662  nt2 = t2 - tanRMin*v.z()*rin ;
1663  nt3 = t3 - rin*rin ;
1664 
1665  // Equation quadratic => 2 roots : first root must be leaving
1666 
1667  b = nt2/nt1 ;
1668  c = nt3/nt1 ;
1669  d = b*b - c ;
1670 
1671  if ( d >= 0.0 )
1672  {
1673  // NOTE: should be rho-rin<kRadTolerance*0.5,
1674  // but using squared versions for efficiency
1675 
1676  if (nt3 < kRadTolerance*(rin + kRadTolerance*0.25))
1677  {
1678  if ( nt2 < 0.0 )
1679  {
1680  if (calcNorm) { *validNorm = false; }
1681  return snxt = 0.0;
1682  }
1683  }
1684  else
1685  {
1686  if (b>0) { sr2 = -b - std::sqrt(d); }
1687  else { sr2 = c/(-b+std::sqrt(d)); }
1688  zi = p.z() + sr2*v.z() ;
1689  ri = tanRMin*zi + rMinAv ;
1690 
1691  if( (ri>=0.0)&&(-halfRadTolerance<=sr2)&&(sr2<=halfRadTolerance) )
1692  {
1693  // An intersection within the tolerance
1694  // storing it in case it is good.
1695 
1696  slentol = sr2 ;
1697  sidetol = kRMax ;
1698  }
1699  if( (ri<0) || (sr2 < halfRadTolerance) )
1700  {
1701  if (b>0) { sr3 = c/(-b-std::sqrt(d)); }
1702  else { sr3 = -b + std::sqrt(d) ; }
1703 
1704  // Safety: if both roots -ve ensure that srd cannot `win'
1705  // distancetoout
1706 
1707  if ( sr3 > halfRadTolerance )
1708  {
1709  if( sr3 < srd )
1710  {
1711  zi = p.z() + sr3*v.z() ;
1712  ri = tanRMin*zi + rMinAv ;
1713 
1714  if ( ri >= 0.0 )
1715  {
1716  srd=sr3 ;
1717  sider=kRMin ;
1718  }
1719  }
1720  }
1721  else if ( sr3 > -halfRadTolerance )
1722  {
1723  // Intersection in tolerance. Store to check if it's good
1724 
1725  slentol = sr3 ;
1726  sidetol = kRMin ;
1727  }
1728  }
1729  else if ( (sr2 < srd) && (sr2 > halfCarTolerance) )
1730  {
1731  srd = sr2 ;
1732  sider = kRMin ;
1733  }
1734  else if (sr2 > -halfCarTolerance)
1735  {
1736  // Intersection in tolerance. Store to check if it's good
1737 
1738  slentol = sr2 ;
1739  sidetol = kRMin ;
1740  }
1741  if( slentol <= halfCarTolerance )
1742  {
1743  // An intersection within the tolerance was found.
1744  // We must accept it only if the momentum points outwards.
1745 
1746  G4ThreeVector Normal ;
1747 
1748  // Calculate a normal vector, as below
1749 
1750  xi = p.x() + slentol*v.x() ;
1751  yi = p.y() + slentol*v.y() ;
1752  if( sidetol==kRMax )
1753  {
1754  risec = std::sqrt(xi*xi + yi*yi)*secRMax ;
1755  Normal = G4ThreeVector(xi/risec,yi/risec,-tanRMax/secRMax) ;
1756  }
1757  else
1758  {
1759  risec = std::sqrt(xi*xi + yi*yi)*secRMin ;
1760  Normal = G4ThreeVector(-xi/risec,-yi/risec,tanRMin/secRMin) ;
1761  }
1762  if( Normal.dot(v) > 0 )
1763  {
1764  // We will leave the cone immediately
1765 
1766  if( calcNorm )
1767  {
1768  *n = Normal.unit() ;
1769  *validNorm = true ;
1770  }
1771  return snxt = 0.0 ;
1772  }
1773  else
1774  {
1775  // On the surface, but not heading out so we ignore this
1776  // intersection (as it is within tolerance).
1777 
1778  slentol = kInfinity ;
1779  }
1780  }
1781  }
1782  }
1783  }
1784  }
1785 
1786  // Linear case => point outside inner cone ---> outer cone intersect
1787  //
1788  // Phi Intersection
1789 
1790  if ( !fPhiFullCone )
1791  {
1792  // add angle calculation with correction
1793  // of the difference in domain of atan2 and Sphi
1794 
1795  vphi = std::atan2(v.y(),v.x()) ;
1796 
1797  if ( vphi < fSPhi - halfAngTolerance ) { vphi += twopi; }
1798  else if ( vphi > fSPhi + fDPhi + halfAngTolerance ) { vphi -= twopi; }
1799 
1800  if ( p.x() || p.y() ) // Check if on z axis (rho not needed later)
1801  {
1802  // pDist -ve when inside
1803 
1804  pDistS = p.x()*sinSPhi - p.y()*cosSPhi ;
1805  pDistE = -p.x()*sinEPhi + p.y()*cosEPhi ;
1806 
1807  // Comp -ve when in direction of outwards normal
1808 
1809  compS = -sinSPhi*v.x() + cosSPhi*v.y() ;
1810  compE = sinEPhi*v.x() - cosEPhi*v.y() ;
1811 
1812  sidephi = kNull ;
1813 
1814  if( ( (fDPhi <= pi) && ( (pDistS <= halfCarTolerance)
1815  && (pDistE <= halfCarTolerance) ) )
1816  || ( (fDPhi > pi) && !((pDistS > halfCarTolerance)
1817  && (pDistE > halfCarTolerance) ) ) )
1818  {
1819  // Inside both phi *full* planes
1820  if ( compS < 0 )
1821  {
1822  sphi = pDistS/compS ;
1823  if (sphi >= -halfCarTolerance)
1824  {
1825  xi = p.x() + sphi*v.x() ;
1826  yi = p.y() + sphi*v.y() ;
1827 
1828  // Check intersecting with correct half-plane
1829  // (if not -> no intersect)
1830  //
1831  if ( (std::fabs(xi)<=kCarTolerance)
1832  && (std::fabs(yi)<=kCarTolerance) )
1833  {
1834  sidephi= kSPhi;
1835  if ( ( fSPhi-halfAngTolerance <= vphi )
1836  && ( fSPhi+fDPhi+halfAngTolerance >=vphi ) )
1837  {
1838  sphi = kInfinity;
1839  }
1840  }
1841  else
1842  if ( (yi*cosCPhi-xi*sinCPhi)>=0 )
1843  {
1844  sphi = kInfinity ;
1845  }
1846  else
1847  {
1848  sidephi = kSPhi ;
1849  if ( pDistS > -halfCarTolerance )
1850  {
1851  sphi = 0.0 ; // Leave by sphi immediately
1852  }
1853  }
1854  }
1855  else
1856  {
1857  sphi = kInfinity ;
1858  }
1859  }
1860  else
1861  {
1862  sphi = kInfinity ;
1863  }
1864 
1865  if ( compE < 0 )
1866  {
1867  sphi2 = pDistE/compE ;
1868 
1869  // Only check further if < starting phi intersection
1870  //
1871  if ( (sphi2 > -halfCarTolerance) && (sphi2 < sphi) )
1872  {
1873  xi = p.x() + sphi2*v.x() ;
1874  yi = p.y() + sphi2*v.y() ;
1875 
1876  // Check intersecting with correct half-plane
1877 
1878  if ( (std::fabs(xi)<=kCarTolerance)
1879  && (std::fabs(yi)<=kCarTolerance) )
1880  {
1881  // Leaving via ending phi
1882 
1883  if(!( (fSPhi-halfAngTolerance <= vphi)
1884  && (fSPhi+fDPhi+halfAngTolerance >= vphi) ) )
1885  {
1886  sidephi = kEPhi ;
1887  if ( pDistE <= -halfCarTolerance ) { sphi = sphi2; }
1888  else { sphi = 0.0; }
1889  }
1890  }
1891  else // Check intersecting with correct half-plane
1892  if ( yi*cosCPhi-xi*sinCPhi >= 0 )
1893  {
1894  // Leaving via ending phi
1895 
1896  sidephi = kEPhi ;
1897  if ( pDistE <= -halfCarTolerance ) { sphi = sphi2; }
1898  else { sphi = 0.0; }
1899  }
1900  }
1901  }
1902  }
1903  else
1904  {
1905  sphi = kInfinity ;
1906  }
1907  }
1908  else
1909  {
1910  // On z axis + travel not || to z axis -> if phi of vector direction
1911  // within phi of shape, Step limited by rmax, else Step =0
1912 
1913  if ( (fSPhi-halfAngTolerance <= vphi)
1914  && (vphi <= fSPhi+fDPhi+halfAngTolerance) )
1915  {
1916  sphi = kInfinity ;
1917  }
1918  else
1919  {
1920  sidephi = kSPhi ; // arbitrary
1921  sphi = 0.0 ;
1922  }
1923  }
1924  if ( sphi < snxt ) // Order intersecttions
1925  {
1926  snxt=sphi ;
1927  side=sidephi ;
1928  }
1929  }
1930  if ( srd < snxt ) // Order intersections
1931  {
1932  snxt = srd ;
1933  side = sider ;
1934  }
1935  if (calcNorm)
1936  {
1937  switch(side)
1938  { // Note: returned vector not normalised
1939  case kRMax: // (divide by frmax for unit vector)
1940  xi = p.x() + snxt*v.x() ;
1941  yi = p.y() + snxt*v.y() ;
1942  risec = std::sqrt(xi*xi + yi*yi)*secRMax ;
1943  *n = G4ThreeVector(xi/risec,yi/risec,-tanRMax/secRMax) ;
1944  *validNorm = true ;
1945  break ;
1946  case kRMin:
1947  *validNorm = false ; // Rmin is inconvex
1948  break ;
1949  case kSPhi:
1950  if ( fDPhi <= pi )
1951  {
1952  *n = G4ThreeVector(sinSPhi, -cosSPhi, 0);
1953  *validNorm = true ;
1954  }
1955  else
1956  {
1957  *validNorm = false ;
1958  }
1959  break ;
1960  case kEPhi:
1961  if ( fDPhi <= pi )
1962  {
1963  *n = G4ThreeVector(-sinEPhi, cosEPhi, 0);
1964  *validNorm = true ;
1965  }
1966  else
1967  {
1968  *validNorm = false ;
1969  }
1970  break ;
1971  case kPZ:
1972  *n = G4ThreeVector(0,0,1) ;
1973  *validNorm = true ;
1974  break ;
1975  case kMZ:
1976  *n = G4ThreeVector(0,0,-1) ;
1977  *validNorm = true ;
1978  break ;
1979  default:
1980  G4cout << G4endl ;
1981  DumpInfo();
1982  std::ostringstream message;
1983  G4int oldprc = message.precision(16) ;
1984  message << "Undefined side for valid surface normal to solid."
1985  << G4endl
1986  << "Position:" << G4endl << G4endl
1987  << "p.x() = " << p.x()/mm << " mm" << G4endl
1988  << "p.y() = " << p.y()/mm << " mm" << G4endl
1989  << "p.z() = " << p.z()/mm << " mm" << G4endl << G4endl
1990  << "pho at z = " << std::sqrt( p.x()*p.x()+p.y()*p.y() )/mm
1991  << " mm" << G4endl << G4endl ;
1992  if( p.x() != 0. || p.y() != 0.)
1993  {
1994  message << "point phi = " << std::atan2(p.y(),p.x())/degree
1995  << " degree" << G4endl << G4endl ;
1996  }
1997  message << "Direction:" << G4endl << G4endl
1998  << "v.x() = " << v.x() << G4endl
1999  << "v.y() = " << v.y() << G4endl
2000  << "v.z() = " << v.z() << G4endl<< G4endl
2001  << "Proposed distance :" << G4endl<< G4endl
2002  << "snxt = " << snxt/mm << " mm" << G4endl ;
2003  message.precision(oldprc) ;
2004  G4Exception("G4Cons::DistanceToOut(p,v,..)","GeomSolids1002",
2005  JustWarning, message) ;
2006  break ;
2007  }
2008  }
2009  if (snxt < halfCarTolerance) { snxt = 0.; }
2010 
2011  return snxt ;
2012 }
kMZ
Definition: G4Cons.cc:76
mm
static constexpr double mm
Definition: G4SIunits.hh:115
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
kRMin
Definition: G4Cons.cc:76
CLHEP::Hep3Vector::x
double x() const
CLHEP::Hep3Vector::dot
double dot(const Hep3Vector &) const
JustWarning
Definition: G4ExceptionSeverity.hh:64
G4int
int G4int
Definition: G4Types.hh:78
CLHEP::Hep3Vector::z
double z() const
kNull
Definition: G4Cons.cc:76
G4VSolid::DumpInfo
void DumpInfo() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
test.b
tuple b
Definition: test.py:12
G4cout
G4GLOB_DLL std::ostream G4cout
kSPhi
Definition: G4Cons.cc:76
degree
static constexpr double degree
Definition: G4SIunits.hh:144
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
CLHEP::Hep3Vector::unit
Hep3Vector unit() const
plottest35.t1
tuple t1
Definition: plottest35.py:33
CLHEP::Hep3Vector::y
double y() const
kPZ
Definition: G4Cons.cc:76
G4endl
#define G4endl
Definition: G4ios.hh:61
G4VSolid::kCarTolerance
G4double kCarTolerance
Definition: G4VSolid.hh:307
pi
static constexpr double pi
Definition: G4SIunits.hh:75
ESide
ESide
Definition: G4Cons.cc:76
kRMax
Definition: G4Cons.cc:76
G4double
double G4double
Definition: G4Types.hh:76
test.c
tuple c
Definition: test.py:13
kEPhi
Definition: G4Cons.cc:76

Here is the call graph for this function:

G4double G4Cons::DistanceToOut ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 2018 of file G4Cons.cc.

2019 {
2020  G4double safe=0.0, rho, safeR1, safeR2, safeZ, safePhi;
2021  G4double tanRMin, secRMin, pRMin;
2022  G4double tanRMax, secRMax, pRMax;
2023 
2024 #ifdef G4CSGDEBUG
2025  if( Inside(p) == kOutside )
2026  {
2027  G4int oldprc=G4cout.precision(16) ;
2028  G4cout << G4endl ;
2029  DumpInfo();
2030  G4cout << "Position:" << G4endl << G4endl ;
2031  G4cout << "p.x() = " << p.x()/mm << " mm" << G4endl ;
2032  G4cout << "p.y() = " << p.y()/mm << " mm" << G4endl ;
2033  G4cout << "p.z() = " << p.z()/mm << " mm" << G4endl << G4endl ;
2034  G4cout << "pho at z = " << std::sqrt( p.x()*p.x()+p.y()*p.y() )/mm
2035  << " mm" << G4endl << G4endl ;
2036  if( (p.x() != 0.) || (p.x() != 0.) )
2037  {
2038  G4cout << "point phi = " << std::atan2(p.y(),p.x())/degree
2039  << " degree" << G4endl << G4endl ;
2040  }
2041  G4cout.precision(oldprc) ;
2042  G4Exception("G4Cons::DistanceToOut(p)", "GeomSolids1002",
2043  JustWarning, "Point p is outside !?" );
2044  }
2045 #endif
2046 
2047  rho = std::sqrt(p.x()*p.x() + p.y()*p.y()) ;
2048  safeZ = fDz - std::fabs(p.z()) ;
2049 
2050  if (fRmin1 || fRmin2)
2051  {
2052  tanRMin = (fRmin2 - fRmin1)*0.5/fDz ;
2053  secRMin = std::sqrt(1.0 + tanRMin*tanRMin) ;
2054  pRMin = tanRMin*p.z() + (fRmin1 + fRmin2)*0.5 ;
2055  safeR1 = (rho - pRMin)/secRMin ;
2056  }
2057  else
2058  {
2059  safeR1 = kInfinity ;
2060  }
2061 
2062  tanRMax = (fRmax2 - fRmax1)*0.5/fDz ;
2063  secRMax = std::sqrt(1.0 + tanRMax*tanRMax) ;
2064  pRMax = tanRMax*p.z() + (fRmax1+fRmax2)*0.5 ;
2065  safeR2 = (pRMax - rho)/secRMax ;
2066 
2067  if (safeR1 < safeR2) { safe = safeR1; }
2068  else { safe = safeR2; }
2069  if (safeZ < safe) { safe = safeZ ; }
2070 
2071  // Check if phi divided, Calc distances closest phi plane
2072 
2073  if (!fPhiFullCone)
2074  {
2075  // Above/below central phi of G4Cons?
2076 
2077  if ( (p.y()*cosCPhi - p.x()*sinCPhi) <= 0 )
2078  {
2079  safePhi = -(p.x()*sinSPhi - p.y()*cosSPhi) ;
2080  }
2081  else
2082  {
2083  safePhi = (p.x()*sinEPhi - p.y()*cosEPhi) ;
2084  }
2085  if (safePhi < safe) { safe = safePhi; }
2086  }
2087  if ( safe < 0 ) { safe = 0; }
2088 
2089  return safe ;
2090 }
mm
static constexpr double mm
Definition: G4SIunits.hh:115
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
CLHEP::Hep3Vector::x
double x() const
G4Cons::Inside
EInside Inside(const G4ThreeVector &p) const
Definition: G4Cons.cc:210
JustWarning
Definition: G4ExceptionSeverity.hh:64
G4int
int G4int
Definition: G4Types.hh:78
CLHEP::Hep3Vector::z
double z() const
G4VSolid::DumpInfo
void DumpInfo() const
G4cout
G4GLOB_DLL std::ostream G4cout
degree
static constexpr double degree
Definition: G4SIunits.hh:144
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
CLHEP::Hep3Vector::y
double y() const
G4endl
#define G4endl
Definition: G4ios.hh:61
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

void G4Cons::Extent ( G4ThreeVector &  pMin,
G4ThreeVector &  pMax 
) const
virtual

Reimplemented from G4VSolid.

Definition at line 276 of file G4Cons.cc.

277 {
278  G4double rmin = std::min(GetInnerRadiusMinusZ(),GetInnerRadiusPlusZ());
279  G4double rmax = std::max(GetOuterRadiusMinusZ(),GetOuterRadiusPlusZ());
280  G4double dz = GetZHalfLength();
281 
282  // Find bounding box
283  //
284  if (GetDeltaPhiAngle() < twopi)
285  {
286  G4TwoVector vmin,vmax;
287  G4GeomTools::DiskExtent(rmin,rmax,
288  GetSinStartPhi(),GetCosStartPhi(),
289  GetSinEndPhi(),GetCosEndPhi(),
290  vmin,vmax);
291  pMin.set(vmin.x(),vmin.y(),-dz);
292  pMax.set(vmax.x(),vmax.y(), dz);
293  }
294  else
295  {
296  pMin.set(-rmax,-rmax,-dz);
297  pMax.set( rmax, rmax, dz);
298  }
299 
300  // Check correctness of the bounding box
301  //
302  if (pMin.x() >= pMax.x() || pMin.y() >= pMax.y() || pMin.z() >= pMax.z())
303  {
304  std::ostringstream message;
305  message << "Bad bounding box (min >= max) for solid: "
306  << GetName() << " !"
307  << "\npMin = " << pMin
308  << "\npMax = " << pMax;
309  G4Exception("G4Cons::Extent()", "GeomMgt0001", JustWarning, message);
310  DumpInfo();
311  }
312 }
CLHEP::Hep3Vector::set
void set(double x, double y, double z)
G4VSolid::GetName
G4String GetName() const
CLHEP::Hep2Vector::y
double y() const
CLHEP::Hep2Vector::x
double x() const
G4Cons::GetSinEndPhi
G4double GetSinEndPhi() const
CLHEP::Hep3Vector::x
double x() const
G4Cons::GetOuterRadiusMinusZ
G4double GetOuterRadiusMinusZ() const
JustWarning
Definition: G4ExceptionSeverity.hh:64
CLHEP::Hep3Vector::z
double z() const
G4VSolid::DumpInfo
void DumpInfo() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4Cons::GetSinStartPhi
G4double GetSinStartPhi() const
G4Cons::GetInnerRadiusPlusZ
G4double GetInnerRadiusPlusZ() const
G4Cons::GetCosEndPhi
G4double GetCosEndPhi() const
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
G4Cons::GetCosStartPhi
G4double GetCosStartPhi() const
G4INCL::Math::max
T max(const T t1, const T t2)
brief Return the largest of the two arguments
Definition: G4INCLGlobals.hh:112
CLHEP::Hep3Vector::y
double y() const
G4INCL::Math::min
T min(const T t1, const T t2)
brief Return the smallest of the two arguments
Definition: G4INCLGlobals.hh:117
G4double
double G4double
Definition: G4Types.hh:76
G4Cons::GetInnerRadiusMinusZ
G4double GetInnerRadiusMinusZ() const
G4Cons::GetOuterRadiusPlusZ
G4double GetOuterRadiusPlusZ() const
G4Cons::GetZHalfLength
G4double GetZHalfLength() const
G4GeomTools::DiskExtent
static G4bool DiskExtent(G4double rmin, G4double rmax, G4double startPhi, G4double delPhi, G4TwoVector &pmin, G4TwoVector &pmax)
Definition: G4GeomTools.cc:378
G4Cons::GetDeltaPhiAngle
G4double GetDeltaPhiAngle() const

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Cons::GetCosEndPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetCosStartPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetCubicVolume ( )
inlinevirtual

Reimplemented from G4VSolid.

G4double G4Cons::GetDeltaPhiAngle ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetDPhi ( ) const
inline
G4double G4Cons::GetDz ( ) const
inline
G4GeometryType G4Cons::GetEntityType ( ) const
virtual

Implements G4VSolid.

Definition at line 2096 of file G4Cons.cc.

2097 {
2098  return G4String("G4Cons");
2099 }
G4double G4Cons::GetInnerRadiusMinusZ ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetInnerRadiusPlusZ ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetOuterRadiusMinusZ ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetOuterRadiusPlusZ ( ) const
inline

Here is the caller graph for this function:

G4ThreeVector G4Cons::GetPointOnSurface ( ) const
virtual

Reimplemented from G4VSolid.

Definition at line 2141 of file G4Cons.cc.

2142 {
2143  // declare working variables
2144  //
2145  G4double Aone, Atwo, Athree, Afour, Afive, slin, slout, phi;
2146  G4double zRand, cosu, sinu, rRand1, rRand2, chose, rone, rtwo, qone, qtwo;
2147  rone = (fRmax1-fRmax2)/(2.*fDz);
2148  rtwo = (fRmin1-fRmin2)/(2.*fDz);
2149  qone=0.; qtwo=0.;
2150  if(fRmax1!=fRmax2) { qone = fDz*(fRmax1+fRmax2)/(fRmax1-fRmax2); }
2151  if(fRmin1!=fRmin2) { qtwo = fDz*(fRmin1+fRmin2)/(fRmin1-fRmin2); }
2152  slin = std::sqrt(sqr(fRmin1-fRmin2)+sqr(2.*fDz));
2153  slout = std::sqrt(sqr(fRmax1-fRmax2)+sqr(2.*fDz));
2154  Aone = 0.5*fDPhi*(fRmax2 + fRmax1)*slout;
2155  Atwo = 0.5*fDPhi*(fRmin2 + fRmin1)*slin;
2156  Athree = 0.5*fDPhi*(fRmax1*fRmax1-fRmin1*fRmin1);
2157  Afour = 0.5*fDPhi*(fRmax2*fRmax2-fRmin2*fRmin2);
2158  Afive = fDz*(fRmax1-fRmin1+fRmax2-fRmin2);
2159 
2160  phi = G4RandFlat::shoot(fSPhi,fSPhi+fDPhi);
2161  cosu = std::cos(phi); sinu = std::sin(phi);
2162  rRand1 = GetRadiusInRing(fRmin1, fRmax1);
2163  rRand2 = GetRadiusInRing(fRmin2, fRmax2);
2164 
2165  if ( (fSPhi == 0.) && fPhiFullCone ) { Afive = 0.; }
2166  chose = G4RandFlat::shoot(0.,Aone+Atwo+Athree+Afour+2.*Afive);
2167 
2168  if( (chose >= 0.) && (chose < Aone) )
2169  {
2170  if(fRmin1 != fRmin2)
2171  {
2172  zRand = G4RandFlat::shoot(-1.*fDz,fDz);
2173  return G4ThreeVector (rtwo*cosu*(qtwo-zRand),
2174  rtwo*sinu*(qtwo-zRand), zRand);
2175  }
2176  else
2177  {
2178  return G4ThreeVector(fRmin1*cosu, fRmin2*sinu,
2179  G4RandFlat::shoot(-1.*fDz,fDz));
2180  }
2181  }
2182  else if( (chose >= Aone) && (chose <= Aone + Atwo) )
2183  {
2184  if(fRmax1 != fRmax2)
2185  {
2186  zRand = G4RandFlat::shoot(-1.*fDz,fDz);
2187  return G4ThreeVector (rone*cosu*(qone-zRand),
2188  rone*sinu*(qone-zRand), zRand);
2189  }
2190  else
2191  {
2192  return G4ThreeVector(fRmax1*cosu, fRmax2*sinu,
2193  G4RandFlat::shoot(-1.*fDz,fDz));
2194  }
2195  }
2196  else if( (chose >= Aone + Atwo) && (chose < Aone + Atwo + Athree) )
2197  {
2198  return G4ThreeVector (rRand1*cosu, rRand1*sinu, -1*fDz);
2199  }
2200  else if( (chose >= Aone + Atwo + Athree)
2201  && (chose < Aone + Atwo + Athree + Afour) )
2202  {
2203  return G4ThreeVector (rRand2*cosu,rRand2*sinu,fDz);
2204  }
2205  else if( (chose >= Aone + Atwo + Athree + Afour)
2206  && (chose < Aone + Atwo + Athree + Afour + Afive) )
2207  {
2208  zRand = G4RandFlat::shoot(-1.*fDz,fDz);
2209  rRand1 = G4RandFlat::shoot(fRmin2-((zRand-fDz)/(2.*fDz))*(fRmin1-fRmin2),
2210  fRmax2-((zRand-fDz)/(2.*fDz))*(fRmax1-fRmax2));
2211  return G4ThreeVector (rRand1*std::cos(fSPhi),
2212  rRand1*std::sin(fSPhi), zRand);
2213  }
2214  else
2215  {
2216  zRand = G4RandFlat::shoot(-1.*fDz,fDz);
2217  rRand1 = G4RandFlat::shoot(fRmin2-((zRand-fDz)/(2.*fDz))*(fRmin1-fRmin2),
2218  fRmax2-((zRand-fDz)/(2.*fDz))*(fRmax1-fRmax2));
2219  return G4ThreeVector (rRand1*std::cos(fSPhi+fDPhi),
2220  rRand1*std::sin(fSPhi+fDPhi), zRand);
2221  }
2222 }
G4INCL::DeJongSpin::shoot
ThreeVector shoot(const G4int Ap, const G4int Af)
Definition: G4INCLDeJongSpin.cc:68
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
G4CSGSolid::GetRadiusInRing
G4double GetRadiusInRing(G4double rmin, G4double rmax) const
Definition: G4CSGSolid.cc:111
sqr
T sqr(const T &x)
Definition: templates.hh:145
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

G4double G4Cons::GetRmax1 ( ) const
inline
G4double G4Cons::GetRmax2 ( ) const
inline
G4double G4Cons::GetRmin1 ( ) const
inline
G4double G4Cons::GetRmin2 ( ) const
inline
G4double G4Cons::GetSinEndPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetSinStartPhi ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetSPhi ( ) const
inline
G4double G4Cons::GetStartPhiAngle ( ) const
inline

Here is the caller graph for this function:

G4double G4Cons::GetSurfaceArea ( )
inlinevirtual

Reimplemented from G4VSolid.

G4double G4Cons::GetZHalfLength ( ) const
inline

Here is the caller graph for this function:

EInside G4Cons::Inside ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 210 of file G4Cons.cc.

211 {
212  G4double r2, rl, rh, pPhi, tolRMin, tolRMax; // rh2, rl2 ;
213  EInside in;
214 
215  if (std::fabs(p.z()) > fDz + halfCarTolerance ) { return in = kOutside; }
216  else if(std::fabs(p.z()) >= fDz - halfCarTolerance ) { in = kSurface; }
217  else { in = kInside; }
218 
219  r2 = p.x()*p.x() + p.y()*p.y() ;
220  rl = 0.5*(fRmin2*(p.z() + fDz) + fRmin1*(fDz - p.z()))/fDz ;
221  rh = 0.5*(fRmax2*(p.z()+fDz)+fRmax1*(fDz-p.z()))/fDz;
222 
223  // rh2 = rh*rh;
224 
225  tolRMin = rl - halfRadTolerance;
226  if ( tolRMin < 0 ) { tolRMin = 0; }
227  tolRMax = rh + halfRadTolerance;
228 
229  if ( (r2<tolRMin*tolRMin) || (r2>tolRMax*tolRMax) ) { return in = kOutside; }
230 
231  if (rl) { tolRMin = rl + halfRadTolerance; }
232  else { tolRMin = 0.0; }
233  tolRMax = rh - halfRadTolerance;
234 
235  if (in == kInside) // else it's kSurface already
236  {
237  if ( (r2 < tolRMin*tolRMin) || (r2 >= tolRMax*tolRMax) ) { in = kSurface; }
238  }
239  if ( !fPhiFullCone && ((p.x() != 0.0) || (p.y() != 0.0)) )
240  {
241  pPhi = std::atan2(p.y(),p.x()) ;
242 
243  if ( pPhi < fSPhi - halfAngTolerance ) { pPhi += twopi; }
244  else if ( pPhi > fSPhi + fDPhi + halfAngTolerance ) { pPhi -= twopi; }
245 
246  if ( (pPhi < fSPhi - halfAngTolerance) ||
247  (pPhi > fSPhi + fDPhi + halfAngTolerance) ) { return in = kOutside; }
248 
249  else if (in == kInside) // else it's kSurface anyway already
250  {
251  if ( (pPhi < fSPhi + halfAngTolerance) ||
252  (pPhi > fSPhi + fDPhi - halfAngTolerance) ) { in = kSurface; }
253  }
254  }
255  else if ( !fPhiFullCone ) { in = kSurface; }
256 
257  return in ;
258 }
CLHEP::Hep3Vector::x
double x() const
CLHEP::Hep3Vector::z
double z() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
EInside
EInside
Definition: geomdefs.hh:58
CLHEP::Hep3Vector::y
double y() const
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

Here is the caller graph for this function:

G4Cons & G4Cons::operator= ( const G4Cons &  rhs)

Definition at line 177 of file G4Cons.cc.

178 {
179  // Check assignment to self
180  //
181  if (this == &rhs) { return *this; }
182 
183  // Copy base class data
184  //
185  G4CSGSolid::operator=(rhs);
186 
187  // Copy data
188  //
189  kRadTolerance = rhs.kRadTolerance;
190  kAngTolerance = rhs.kAngTolerance;
191  fRmin1 = rhs.fRmin1; fRmin2 = rhs.fRmin2;
192  fRmax1 = rhs.fRmax1; fRmax2 = rhs.fRmax2;
193  fDz = rhs.fDz; fSPhi = rhs.fSPhi; fDPhi = rhs.fDPhi;
194  sinCPhi = rhs.sinCPhi; cosCPhi = rhs.cosCPhi;
195  cosHDPhiOT = rhs.cosHDPhiOT; cosHDPhiIT = rhs.cosHDPhiIT;
196  sinSPhi = rhs.sinSPhi; cosSPhi = rhs.cosSPhi;
197  sinEPhi = rhs.sinEPhi; cosEPhi = rhs.cosEPhi;
198  fPhiFullCone = rhs.fPhiFullCone;
199  halfCarTolerance = rhs.halfCarTolerance;
200  halfRadTolerance = rhs.halfRadTolerance;
201  halfAngTolerance = rhs.halfAngTolerance;
202 
203  return *this;
204 }
G4CSGSolid::operator=
G4CSGSolid & operator=(const G4CSGSolid &rhs)
Definition: G4CSGSolid.cc:91

Here is the call graph for this function:

void G4Cons::SetDeltaPhiAngle ( G4double  newDPhi)
inline

Here is the caller graph for this function:

void G4Cons::SetInnerRadiusMinusZ ( G4double  Rmin1)
inline

Here is the caller graph for this function:

void G4Cons::SetInnerRadiusPlusZ ( G4double  Rmin2)
inline

Here is the caller graph for this function:

void G4Cons::SetOuterRadiusMinusZ ( G4double  Rmax1)
inline

Here is the caller graph for this function:

void G4Cons::SetOuterRadiusPlusZ ( G4double  Rmax2)
inline

Here is the caller graph for this function:

void G4Cons::SetStartPhiAngle ( G4double  newSPhi,
G4bool  trig = true 
)
inline

Here is the caller graph for this function:

void G4Cons::SetZHalfLength ( G4double  newDz)
inline

Here is the caller graph for this function:

std::ostream & G4Cons::StreamInfo ( std::ostream &  os) const
virtual

Reimplemented from G4CSGSolid.

Definition at line 2114 of file G4Cons.cc.

2115 {
2116  G4int oldprc = os.precision(16);
2117  os << "-----------------------------------------------------------\n"
2118  << " *** Dump for solid - " << GetName() << " ***\n"
2119  << " ===================================================\n"
2120  << " Solid type: G4Cons\n"
2121  << " Parameters: \n"
2122  << " inside -fDz radius: " << fRmin1/mm << " mm \n"
2123  << " outside -fDz radius: " << fRmax1/mm << " mm \n"
2124  << " inside +fDz radius: " << fRmin2/mm << " mm \n"
2125  << " outside +fDz radius: " << fRmax2/mm << " mm \n"
2126  << " half length in Z : " << fDz/mm << " mm \n"
2127  << " starting angle of segment: " << fSPhi/degree << " degrees \n"
2128  << " delta angle of segment : " << fDPhi/degree << " degrees \n"
2129  << "-----------------------------------------------------------\n";
2130  os.precision(oldprc);
2131 
2132  return os;
2133 }
G4VSolid::GetName
G4String GetName() const
mm
static constexpr double mm
Definition: G4SIunits.hh:115
G4int
int G4int
Definition: G4Types.hh:78
degree
static constexpr double degree
Definition: G4SIunits.hh:144

Here is the call graph for this function:

G4ThreeVector G4Cons::SurfaceNormal ( const G4ThreeVector &  p) const
virtual

Implements G4VSolid.

Definition at line 433 of file G4Cons.cc.

434 {
435  G4int noSurfaces = 0;
436  G4double rho, pPhi;
437  G4double distZ, distRMin, distRMax;
438  G4double distSPhi = kInfinity, distEPhi = kInfinity;
439  G4double tanRMin, secRMin, pRMin, widRMin;
440  G4double tanRMax, secRMax, pRMax, widRMax;
441 
442  G4ThreeVector norm, sumnorm(0.,0.,0.), nZ = G4ThreeVector(0.,0.,1.);
443  G4ThreeVector nR, nr(0.,0.,0.), nPs, nPe;
444 
445  distZ = std::fabs(std::fabs(p.z()) - fDz);
446  rho = std::sqrt(p.x()*p.x() + p.y()*p.y());
447 
448  tanRMin = (fRmin2 - fRmin1)*0.5/fDz;
449  secRMin = std::sqrt(1 + tanRMin*tanRMin);
450  pRMin = rho - p.z()*tanRMin;
451  widRMin = fRmin2 - fDz*tanRMin;
452  distRMin = std::fabs(pRMin - widRMin)/secRMin;
453 
454  tanRMax = (fRmax2 - fRmax1)*0.5/fDz;
455  secRMax = std::sqrt(1+tanRMax*tanRMax);
456  pRMax = rho - p.z()*tanRMax;
457  widRMax = fRmax2 - fDz*tanRMax;
458  distRMax = std::fabs(pRMax - widRMax)/secRMax;
459 
460  if (!fPhiFullCone) // Protected against (0,0,z)
461  {
462  if ( rho )
463  {
464  pPhi = std::atan2(p.y(),p.x());
465 
466  if (pPhi < fSPhi-halfCarTolerance) { pPhi += twopi; }
467  else if (pPhi > fSPhi+fDPhi+halfCarTolerance) { pPhi -= twopi; }
468 
469  distSPhi = std::fabs( pPhi - fSPhi );
470  distEPhi = std::fabs( pPhi - fSPhi - fDPhi );
471  }
472  else if( !(fRmin1) || !(fRmin2) )
473  {
474  distSPhi = 0.;
475  distEPhi = 0.;
476  }
477  nPs = G4ThreeVector(std::sin(fSPhi), -std::cos(fSPhi), 0);
478  nPe = G4ThreeVector(-std::sin(fSPhi+fDPhi), std::cos(fSPhi+fDPhi), 0);
479  }
480  if ( rho > halfCarTolerance )
481  {
482  nR = G4ThreeVector(p.x()/rho/secRMax, p.y()/rho/secRMax, -tanRMax/secRMax);
483  if (fRmin1 || fRmin2)
484  {
485  nr = G4ThreeVector(-p.x()/rho/secRMin,-p.y()/rho/secRMin,tanRMin/secRMin);
486  }
487  }
488 
489  if( distRMax <= halfCarTolerance )
490  {
491  noSurfaces ++;
492  sumnorm += nR;
493  }
494  if( (fRmin1 || fRmin2) && (distRMin <= halfCarTolerance) )
495  {
496  noSurfaces ++;
497  sumnorm += nr;
498  }
499  if( !fPhiFullCone )
500  {
501  if (distSPhi <= halfAngTolerance)
502  {
503  noSurfaces ++;
504  sumnorm += nPs;
505  }
506  if (distEPhi <= halfAngTolerance)
507  {
508  noSurfaces ++;
509  sumnorm += nPe;
510  }
511  }
512  if (distZ <= halfCarTolerance)
513  {
514  noSurfaces ++;
515  if ( p.z() >= 0.) { sumnorm += nZ; }
516  else { sumnorm -= nZ; }
517  }
518  if ( noSurfaces == 0 )
519  {
520 #ifdef G4CSGDEBUG
521  G4Exception("G4Cons::SurfaceNormal(p)", "GeomSolids1002",
522  JustWarning, "Point p is not on surface !?" );
523 #endif
524  norm = ApproxSurfaceNormal(p);
525  }
526  else if ( noSurfaces == 1 ) { norm = sumnorm; }
527  else { norm = sumnorm.unit(); }
528 
529  return norm ;
530 }
kInfinity
static const G4double kInfinity
Definition: geomdefs.hh:42
G4ThreeVector
CLHEP::Hep3Vector G4ThreeVector
Definition: G4ThreeVector.hh:42
CLHEP::Hep3Vector::x
double x() const
JustWarning
Definition: G4ExceptionSeverity.hh:64
G4int
int G4int
Definition: G4Types.hh:78
CLHEP::Hep3Vector::z
double z() const
twopi
static constexpr double twopi
Definition: G4SIunits.hh:76
G4Exception
void G4Exception(const char *originOfException, const char *exceptionCode, G4ExceptionSeverity severity, const char *comments)
Definition: G4Exception.cc:41
CLHEP::Hep3Vector::unit
Hep3Vector unit() const
CLHEP::Hep3Vector::y
double y() const
G4double
double G4double
Definition: G4Types.hh:76

Here is the call graph for this function:

The documentation for this class was generated from the following files: