G4PolynomialPDF Class Reference

#include <G4PolynomialPDF.hh>

Public Member Functions
	G4PolynomialPDF (size_t n=0, const double *coeffs=nullptr, G4double x1=0, G4double x2=1)
	~G4PolynomialPDF ()
void	SetNCoefficients (size_t n)
size_t	GetNCoefficients () const
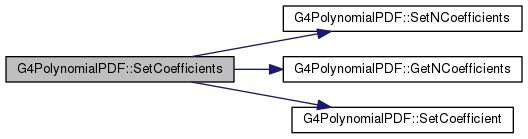
void	SetCoefficients (const std::vector< G4double > &v)
G4double	GetCoefficient (size_t i) const
void	SetCoefficient (size_t i, G4double value)
void	SetCoefficients (size_t n, const G4double *coeffs)
void	SetDomain (G4double x1, G4double x2)
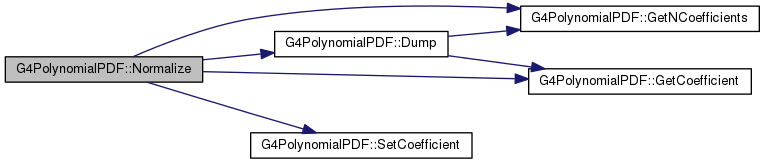
void	Normalize ()
G4double	Evaluate (G4double x, G4int ddxPower=0)
G4double	GetRandomX ()
void	SetTolerance (G4double tolerance)
G4double	GetX (G4double p, G4double x1, G4double x2, G4int ddxPower=0, G4double guess=1.e99, G4bool bisect=true)
G4double	EvalInverseCDF (G4double p)
G4double	Bisect (G4double p, G4double x1, G4double x2)
void	Dump ()

Protected Member Functions
G4bool	HasNegativeMinimum (G4double x1, G4double x2)

Protected Attributes
G4double	fX1
G4double	fX2
std::vector< G4double >	fCoefficients
G4bool	fChanged
G4double	fTolerance
G4int	fVerbose

Detailed Description

Definition at line 49 of file G4PolynomialPDF.hh.

Constructor & Destructor Documentation

G4PolynomialPDF::G4PolynomialPDF	(	size_t	n = 0,
		const double *	coeffs = nullptr,
		G4double	x1 = 0,
		G4double	x2 = 1
	)

Definition at line 43 of file G4PolynomialPDF.cc.

                                           :
  fX1(x1), fX2(x2), fChanged(true), fTolerance(1.e-8), fVerbose(0)
{
  if(coeffs != nullptr) SetCoefficients(n, coeffs);
  else if(n > 0) SetNCoefficients(n);
}

Here is the call graph for this function:

G4PolynomialPDF::~G4PolynomialPDF

(

)

Definition at line 51 of file G4PolynomialPDF.cc.

{}

Member Function Documentation

G4double G4PolynomialPDF::Bisect	(	G4double	p,
		G4double	x1,
		G4double	x2
	)

Definition at line 363 of file G4PolynomialPDF.cc.

                                                                       {
  // Bisect to get 1% precision, then use Newton-Raphson
  G4double z = (x2 + x1)/2.0; // [x1 z x2]
  if((x2 - x1)/(fX2 - fX1) < 0.01) return GetX(p, fX1, fX2, -1, z, false);
  G4double fz = Evaluate(z, -1) - p;
  if(fz < 0) return Bisect(p, z, x2); // [z x2]
  return Bisect(p, x1, z); // [x1 z]
}

Here is the call graph for this function:

Here is the caller graph for this function:

void G4PolynomialPDF::Dump

(

)

Definition at line 372 of file G4PolynomialPDF.cc.

{
  G4cout << "G4PolynomialPDF::Dump() - PDF(x) = ";
  for(size_t i=0; i<GetNCoefficients(); i++) {
    if(i>0) G4cout << " + ";
    G4cout << GetCoefficient(i);
    if(i>0) G4cout << "*x";
    if(i>1) G4cout << "^" << i;
  }
  G4cout << G4endl;
  G4cout << "G4PolynomialPDF::Dump() - Interval: " << fX1 << " <= x < " 
     << fX2 << G4endl;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4PolynomialPDF::EvalInverseCDF ( G4double  p )

inline

Definition at line 99 of file G4PolynomialPDF.hh.

{ return GetX(p, fX1, fX2, -1, fX1 + p*(fX2-fX1)); }

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4PolynomialPDF::Evaluate	(	G4double	x,
		G4int	ddxPower = 0
	)

Evaluate f(x) ddxPower = -1: f = CDF ddxPower = 0: f = PDF ddxPower = 1: f = (d/dx) PDF ddxPower = 2: f = (d2/dx2) PDF

Definition at line 116 of file G4PolynomialPDF.cc.

{
  if(ddxPower < -1 || ddxPower > 2) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: ddxPower " << ddxPower 
         << " not implemented" << G4endl;
    }
    return 0.0;
  }

  double f = 0.; // return value
  double xN = 1.; // x to the power N
  double x1N = 1.; // endpoint x1 to the power N; only used by CDF
  for(size_t i=0; i<=GetNCoefficients(); ++i) {
    if(ddxPower == -1) { // CDF
      if(i>0) f += GetCoefficient(i-1)*(xN - x1N)/i;
      x1N *= fX1;
    }
    else if(ddxPower == 0 && i<GetNCoefficients()) f += GetCoefficient(i)*xN; // PDF
    else if(ddxPower == 1) { // (d/dx) PDF
      if(i<GetNCoefficients()-1) f += GetCoefficient(i+1)*xN*(i+1);
    }
    else if(ddxPower == 2) { // (d2/dx2) PDF
      if(i<GetNCoefficients()-2) f += GetCoefficient(i+2)*xN*((i+2)*(i+1));
    }
    xN *= x;
  }
  return f;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4PolynomialPDF::GetCoefficient ( size_t  i ) const

inline

Definition at line 60 of file G4PolynomialPDF.hh.

{ return fCoefficients[i]; }

Here is the caller graph for this function:

size_t G4PolynomialPDF::GetNCoefficients ( ) const

inline

Definition at line 58 of file G4PolynomialPDF.hh.

{ return fCoefficients.size(); }

Here is the caller graph for this function:

G4double G4PolynomialPDF::GetRandomX

(

)

Definition at line 192 of file G4PolynomialPDF.cc.

{
  if(fChanged) {
    Normalize(); 
    if(HasNegativeMinimum(fX1, fX2)) {
      if(fVerbose > 0) {
    G4cout << "G4PolynomialPDF::GetRandomX() WARNING: PDF has negative values, returning 0..." 
           << G4endl;
      }
      return 0.0;
    }
    fChanged = false;
  }
  return EvalInverseCDF(G4UniformRand());
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4PolynomialPDF::GetX	(	G4double	p,
		G4double	x1,
		G4double	x2,
		G4int	ddxPower = 0,
		G4double	guess = 1.e99,
		G4bool	bisect = true
	)

Find a value of X between x1 and x2 at which f(x) = p. ddxPower = -1: f = CDF ddxPower = 0: f = PDF ddxPower = 1: f = (d/dx) PDF Uses the Newton-Raphson method to find the zero of f(x) - p. If not found in range, returns the nearest boundary

Definition at line 208 of file G4PolynomialPDF.cc.

{

  // input range checking
  if(GetNCoefficients() == 0) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: no PDF defined!" << G4endl;
    }
    return x2;
  }
  if(ddxPower < -1 || ddxPower > 1) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: ddxPower " << ddxPower 
         << " not implemented" << G4endl;
    }
    return x2;
  }
  if(ddxPower == -1 && (p<0 || p>1)) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: p is out of range" << G4endl;
    }
    return fX2;
  }

  // check limits
  if(x2 <= x1 || x1 < fX1 || x2 > fX2) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: domain must have fX1 <= x1 < x2 <= fX2. "
         << "You sent x1 = " << x1 << ", x2 = " << x2 << "." << G4endl;
    }
    return x2;
  }

  // Return x2 for flat lines
  if((ddxPower == 0 && GetNCoefficients() == 1) ||
     (ddxPower == 1 && GetNCoefficients() == 2)) return x2;

  // Solve p = mx + b -> x = (p-b)/m for linear functions
  if((ddxPower == -1 && GetNCoefficients() == 1) ||
     (ddxPower ==  0 && GetNCoefficients() == 2) ||
     (ddxPower ==  1 && GetNCoefficients() == 3)) {
    G4double b = (ddxPower > -1) ? GetCoefficient(ddxPower) : -GetCoefficient(0)*fX1;
    G4double slope = GetCoefficient(ddxPower+1);
    if(ddxPower == 1) slope *= 2.;
    G4double value = (p-b)/slope;
    if(value < x1) {
      return x1;
    }
    else if(value > x2) {
      return x2;
    }
    else {
      return value;
    }
  }

  // Solve quadratic equation for f-p=0 when f is quadratic
  if((ddxPower == -1 && GetNCoefficients() == 2) ||
     (ddxPower ==  0 && GetNCoefficients() == 3) ||
     (ddxPower ==  1 && GetNCoefficients() == 4)) {
    G4double c = -p + ((ddxPower > -1) ? GetCoefficient(ddxPower) : 0);
    if(ddxPower == -1) c -= (GetCoefficient(0) + GetCoefficient(1)/2.*fX1)*fX1;
    G4double b = GetCoefficient(ddxPower+1);
    if(ddxPower == 1) b *= 2.;
    G4double a = GetCoefficient(ddxPower+2);
    if(ddxPower == 1) a *= 3;
    else if(ddxPower == -1) a *= 0.5;
    double sqrtFactor = b*b - 4.*a*c;
    if(sqrtFactor < 0) return x2; // quadratic equation has no solution (p not in range of f)
    sqrtFactor = sqrt(sqrtFactor)/2./fabs(a);
    G4double valueMinus = -b/2./a - sqrtFactor;
    if(valueMinus >= x1 && valueMinus <= x2) return valueMinus;
    else if(valueMinus > x2) return x2;
    G4double valuePlus = -b/2./a + sqrtFactor;
    if(valuePlus >= x1 && valuePlus <= x2) return valuePlus;
    else if(valuePlus < x1) return x2;
    return (x1-valueMinus <= valuePlus-x2) ? x1 : x2;
  }

  // f is non-trivial, so use Newton-Raphson
  // start in the middle if no good guess is provided
  if(guess < x1 || guess > x2) guess = (x2+x1)*0.5; 
  G4double lastChange = 1;
  size_t iterations = 0;
  while(fabs(lastChange) > fTolerance) {  /* Loop checking, 02.11.2015, A.Ribon */
    // calculate f and f' simultaneously
    G4double f = -p;
    G4double dfdx = 0;
    G4double xN = 1;
    G4double x1N = 1; // only used by CDF
    for(size_t i=0; i<=GetNCoefficients(); ++i) {
      if(ddxPower == -1) { // CDF
        if(i>0) f += GetCoefficient(i-1)*(xN - x1N)/G4double(i);
        if(i<GetNCoefficients()) dfdx += GetCoefficient(i)*xN;
        x1N *= fX1;
      }
      else if(ddxPower == 0) { // PDF
        if(i<GetNCoefficients()) f += GetCoefficient(i)*xN;
        if(i+1<GetNCoefficients()) dfdx += GetCoefficient(i+1)*xN*G4double(i+1);
      }
      else { // ddxPower == 1: (d/dx) PDF
        if(i+1<GetNCoefficients()) f += GetCoefficient(i+1)*xN*G4double(i+1);
        if(i+2<GetNCoefficients()) dfdx += GetCoefficient(i+2)*xN*G4double(i+2);
      }
      xN *= guess;
    }
    if(f == 0) return guess;
    if(dfdx == 0) {
      if(fVerbose > 0) {
    G4cout << "G4PolynomialPDF::GetX() WARNING: got f != 0 but slope = 0 for ddxPower = " 
           << ddxPower << G4endl;
      }
      return x2;
    }
    lastChange = - f/dfdx;

    if(guess + lastChange < x1) {
      lastChange = x1 - guess;
    } else if(guess + lastChange > x2) {
      lastChange = x2 - guess;
    }

    guess += lastChange;
    lastChange /= (fX2-fX1);
     
    ++iterations;
    if(iterations > 50) {
      if(p!=0) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: got stuck searching for " << p 
         << " between " << x1 << " and " << x2 << " with ddxPower = " 
         << ddxPower 
         << ". Last guess was " << guess << "." << G4endl;
    }
      }
      if(ddxPower==-1 && bisect) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::GetX() WARNING: Bisceting and trying again..." 
         << G4endl;
    }
        return Bisect(p, x1, x2);
      }
      else return guess;
    }
  }
  return guess;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4bool G4PolynomialPDF::HasNegativeMinimum ( G4double  x1, G4double  x2  )

protected

Definition at line 151 of file G4PolynomialPDF.cc.

{
  // ax2 + bx + c = 0
  // p': 2ax + b = 0 -> = 0 at min: x_extreme = -b/2a

  if(x1 < fX1 || x2 > fX2 || x2 < x1) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::HasNegativeMinimum() WARNING: Invalid range " 
         << x1 << " - " << x2 << G4endl;
    }
    return false;
  }

  // If flat, then check anywhere.
  if(GetNCoefficients() == 1) return (Evaluate(x1) < -fTolerance);

  // If linear, or if quadratic with negative second derivative, 
  // just check the endpoints
  if(GetNCoefficients() == 2 || 
     (GetNCoefficients() == 3 && GetCoefficient(2) < 0)) {
    return (Evaluate(x1) < -fTolerance) || (Evaluate(x2) < -fTolerance);
  }

  // If quadratic and second dervative is positive, check at the mininum
  if(GetNCoefficients() == 3) {
    G4double xMin = -GetCoefficient(1)*0.5/GetCoefficient(2);
    if(xMin < x1) xMin = x1;
    if(xMin > x2) xMin = x2;
    return Evaluate(xMin) < -fTolerance;
  }

  // Higher-order polynomials: consider any extremum between x1 and x2. If none
  // are found, check the endpoints.
  G4double extremum = GetX(0, x1, x2, 1);
  if(Evaluate(extremum) < -fTolerance) return true;
  else if(extremum <= x1+(x2-x1)*fTolerance || 
      extremum >= x2-(x2-x1)*fTolerance) return false;
  else return 
     HasNegativeMinimum(x1, extremum) || HasNegativeMinimum(extremum, x2);
}

Here is the call graph for this function:

Here is the caller graph for this function:

void G4PolynomialPDF::Normalize

(

)

Normalize PDF to 1 over domain fX1 to fX2. Double-check that the highest-order coefficient is non-zero.

Definition at line 86 of file G4PolynomialPDF.cc.

{
  while(fCoefficients.size()) {  /* Loop checking, 30-Oct-2015, G.Folger */
    if(fCoefficients[fCoefficients.size()-1] == 0.0) fCoefficients.pop_back();
    else break;
  }

  G4double x1N = fX1, x2N = fX2;
  G4double sum = 0;
  for(size_t i=0; i<GetNCoefficients(); ++i) {
    sum += GetCoefficient(i)*(x2N - x1N)/G4double(i+1);
    x1N*=fX1;
    x2N*=fX2;
  }
  if(sum <= 0) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::Normalize() WARNING: PDF has non-positive area: " 
         << sum << G4endl;
      Dump();
    }
    return;
  }

  for(size_t i=0; i<GetNCoefficients(); ++i) {
    SetCoefficient(i, GetCoefficient(i)/sum);
  }
}

Here is the call graph for this function:

Here is the caller graph for this function:

void G4PolynomialPDF::SetCoefficient	(	size_t	i,
		G4double	value
	)

Definition at line 54 of file G4PolynomialPDF.cc.

{
  while(i >= fCoefficients.size()) fCoefficients.push_back(0);  
  /* Loop checking, 30-Oct-2015, G.Folger */
  fCoefficients[i] = value;
  fChanged = true;
}

Here is the caller graph for this function:

void G4PolynomialPDF::SetCoefficients ( const std::vector< G4double > &  v )

inline

Definition at line 59 of file G4PolynomialPDF.hh.

{ fCoefficients = v; }

Here is the caller graph for this function:

void G4PolynomialPDF::SetCoefficients	(	size_t	n,
		const G4double *	coeffs
	)

Definition at line 62 of file G4PolynomialPDF.cc.

{
  SetNCoefficients(nCoeffs);
  for(size_t i=0; i<GetNCoefficients(); ++i) {
    SetCoefficient(i, coefficients[i]);
  }
  fChanged = true;
}

Here is the call graph for this function:

void G4PolynomialPDF::SetDomain	(	G4double	x1,
		G4double	x2
	)

Definition at line 72 of file G4PolynomialPDF.cc.

{ 
  if(x2 <= x1) {
    if(fVerbose > 0) {
      G4cout << "G4PolynomialPDF::SetDomain() WARNING: Invalide domain! "
         << "(x1 = " << x1 << ", x2 = " << x2 << ")." << G4endl;
    }
    return;
  }
  fX1 = x1; 
  fX2 = x2; 
  fChanged = true; 
}

void G4PolynomialPDF::SetNCoefficients ( size_t  n )

inline

Definition at line 57 of file G4PolynomialPDF.hh.

{ fCoefficients.resize(n); fChanged = true; }

Here is the caller graph for this function:

void G4PolynomialPDF::SetTolerance ( G4double  tolerance )

inline

Definition at line 84 of file G4PolynomialPDF.hh.

{ fTolerance = tolerance; }

Member Data Documentation

G4bool G4PolynomialPDF::fChanged

protected

Definition at line 111 of file G4PolynomialPDF.hh.

std::vector<G4double> G4PolynomialPDF::fCoefficients

protected

Definition at line 110 of file G4PolynomialPDF.hh.

G4double G4PolynomialPDF::fTolerance

protected

Definition at line 112 of file G4PolynomialPDF.hh.

G4int G4PolynomialPDF::fVerbose

protected

Definition at line 113 of file G4PolynomialPDF.hh.

G4double G4PolynomialPDF::fX1

protected

Definition at line 108 of file G4PolynomialPDF.hh.

G4double G4PolynomialPDF::fX2

protected

Definition at line 109 of file G4PolynomialPDF.hh.

---

The documentation for this class was generated from the following files:

• geant4.10.03.p01/source/processes/hadronic/models/util/include/G4PolynomialPDF.hh
• geant4.10.03.p01/source/processes/hadronic/models/util/src/G4PolynomialPDF.cc