G4Bessel Class Reference

#include <G4Bessel.hh>

Public Member Functions
	G4Bessel ()
	~G4Bessel ()
G4double	I0 (G4double)
G4double	I1 (G4double)
G4double	K0 (G4double)
G4double	K1 (G4double)
G4double	pI0 (G4double)
G4double	pI1 (G4double)
G4double	pK0 (G4double)
G4double	pK1 (G4double)

Detailed Description

Definition at line 66 of file G4Bessel.hh.

Constructor & Destructor Documentation

G4Bessel::G4Bessel

(

)

Definition at line 72 of file G4Bessel.cc.

{;}

G4Bessel::~G4Bessel

(

)

Definition at line 76 of file G4Bessel.cc.

{;}

Member Function Documentation

G4double G4Bessel::I0

(

G4double

x

)

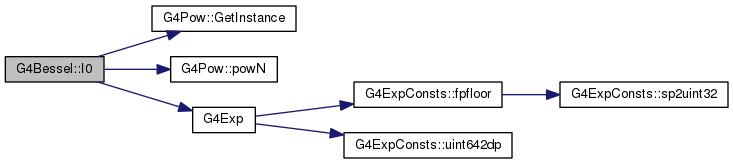
Definition at line 80 of file G4Bessel.cc.

{
  const G4double P1 = 1.0,
                 P2 = 3.5156229,
                 P3 = 3.0899424,
                 P4 = 1.2067492,
                 P5 = 0.2659732,
                 P6 = 0.0360768,
                 P7 = 0.0045813;
  const G4double Q1 = 0.39894228,
                 Q2 = 0.01328592,
                 Q3 = 0.00225319,
                 Q4 =-0.00157565,
                 Q5 = 0.00916281,
                 Q6 =-0.02057706,
                 Q7 = 0.02635537,
                 Q8 =-0.01647633,
                 Q9 = 0.00392377;
  
  G4double I = 0.0;
  if (std::fabs(x) < 3.75)
  {
    G4double y = G4Pow::GetInstance()->powN(x/3.75, 2);
    I = P1+y*(P2+y*(P3+y*(P4+y*(P5+y*(P6+y*P7)))));
  }
  else
  {
    G4double ax = std::fabs(x);
    G4double y  = 3.75/ax;
    I  = G4Exp(ax) / std::sqrt(ax) *
      (Q1+y*(Q2+y*(Q3+y*(Q4+y*(Q5+y*(Q6+y*(Q7+y*(Q8+y*Q9))))))));
  }
  return I;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Bessel::I1

(

G4double

x

)

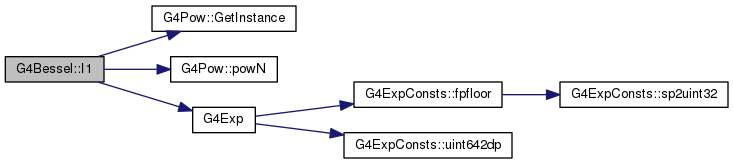
Definition at line 150 of file G4Bessel.cc.

{
  const G4double P1 = 0.5,
                 P2 = 0.87890594,
                 P3 = 0.51498869,
                 P4 = 0.15084934,
                 P5 = 0.02658733,
                 P6 = 0.00301532,
                 P7 = 0.00032411;
  const G4double Q1 = 0.39894228,
                 Q2 =-0.03988024,
                 Q3 =-0.00362018,
                 Q4 = 0.00163801,
                 Q5 =-0.01031555,
                 Q6 = 0.02282967,
                 Q7 =-0.02895312,
                 Q8 = 0.01787654,
                 Q9 =-0.00420059;

  G4double I = 0.0;
  if (std::fabs(x) < 3.75)
  {
    G4double ax = std::fabs(x);
    G4double y = G4Pow::GetInstance()->powN(x/3.75, 2);
    I = ax*(P1+y*(P2+y*(P3+y*(P4+y*(P5+y*(P6+y*P7))))));
  }
  else
  {
    G4double ax = std::fabs(x);
    G4double y  = 3.75/ax;
    I  = G4Exp(ax) / std::sqrt(ax) *
      (Q1+y*(Q2+y*(Q3+y*(Q4+y*(Q5+y*(Q6+y*(Q7+y*(Q8+y*Q9))))))));
  }
  if (x < 0.0) I = -I;
  return I;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Bessel::K0

(

G4double

x

)

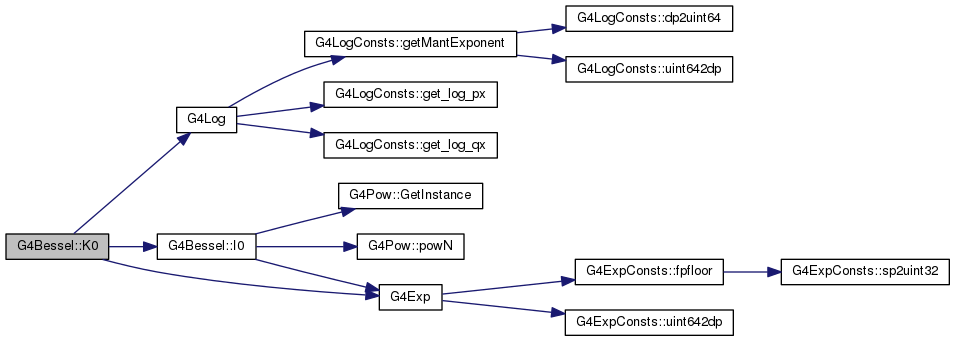
Definition at line 116 of file G4Bessel.cc.

{
  const G4double P1 =-0.57721566,
                 P2 = 0.42278420,
                 P3 = 0.23069756,
                 P4 = 0.03488590,
                 P5 = 0.00262698,
                 P6 = 0.00010750,
                 P7 = 0.00000740;
  const G4double Q1 = 1.25331414,
                 Q2 =-0.07832358,
                 Q3 = 0.02189568,
                 Q4 =-0.01062446,
                 Q5 = 0.00587872,
                 Q6 =-0.00251540,
                 Q7 = 0.00053208;

  G4double K = 0.0;
  if (x <= 2.0)
  {
    G4double y = x * x / 4.0;
    K = (-G4Log(x/2.0)) * I0(x) +
      P1+y*(P2+y*(P3+y*(P4+y*(P5+y*(P6+y*P7)))));
  }
  else
  {
    G4double y = 2.0 / x;
    K = G4Exp(-x)  / std::sqrt(x) *
      (Q1+y*(Q2+y*(Q3+y*(Q4+y*(Q5+y*(Q6+y*Q7))))));
  }
  return K;
}

Here is the call graph for this function:

G4double G4Bessel::K1

(

G4double

x

)

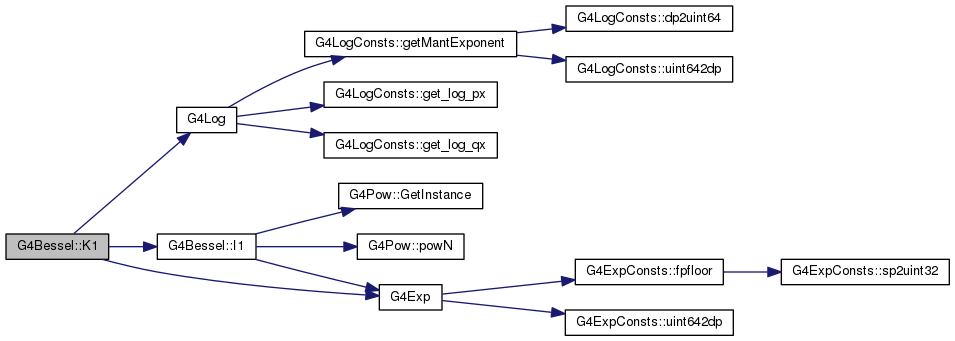
Definition at line 188 of file G4Bessel.cc.

{
  const G4double P1 = 1.0,
                 P2 = 0.15443144,
                 P3 =-0.67278579,
                 P4 =-0.18156897,
                 P5 =-0.01919402,
                 P6 =-0.00110404,
                 P7 =-0.00004686;
  const G4double Q1 = 1.25331414,
                 Q2 = 0.23498619,
                 Q3 =-0.03655620,
                 Q4 = 0.01504268,
                 Q5 =-0.00780353,
                 Q6 = 0.00325614,
                 Q7 =-0.00068245;

  G4double K = 0.0;
  if (x <= 2.0)
  {
    G4double y = x * x / 4.0;
    K = G4Log(x/2.0)*I1(x) + 1.0/x *
      (P1+y*(P2+y*(P3+y*(P4+y*(P5+y*(P6+y*P7))))));
  }
  else
  {
    G4double y = 2.0 / x;
    K = G4Exp(-x) / std::sqrt(x) *
      (Q1+y*(Q2+y*(Q3+y*(Q4+y*(Q5+y*(Q6+y*Q7))))));
  }
  return K;
}

Here is the call graph for this function:

G4double G4Bessel::pI0

(

G4double

x

)

Definition at line 222 of file G4Bessel.cc.

{
  const G4double A0  = 0.1250000000000E+00,
                 A1  = 7.0312500000000E-02,
                 A2  = 7.3242187500000E-02,
                 A3  = 1.1215209960938E-01,
                 A4  = 2.2710800170898E-01,
                 A5  = 5.7250142097473E-01,
                 A6  = 1.7277275025845E+00,
                 A7  = 6.0740420012735E+00,
                 A8  = 2.4380529699556E+01,
                 A9  = 1.1001714026925E+02,
                 A10 = 5.5133589612202E+02,
                 A11 = 3.0380905109224E+03;

  G4double I = 0.0;
  if (x == 0.0)
  {
    I = 1.0;
  }
  else if (x < 18.0)
  {
    I          = 1.0;
    G4double y = x * x;
    G4double q = 1.0;
    for (G4int i=1; i<101; i++)
    {
      q *= 0.25 * y / i / i;
      I += q;
      if (std::abs(q/I) < 1.0E-15) break;
    }
  }
  else
  {
    G4double y = 1.0 / x;
    I = G4Exp(x) / std::sqrt(twopi*x) *
      (1.0 + y*(A0+y*(A1+y*(A2+y*(A3+y*(A4+y*(A5+y*(A6+y*(A7+y*(A8+y*(A9+y*(A10+y*A11))))))))))));
  }

  return I;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Bessel::pI1

(

G4double

x

)

Definition at line 265 of file G4Bessel.cc.

{
  const G4double A0  = -0.3750000000000E+00,
                 A1  = -1.1718750000000E-01,
                 A2  = -1.0253906250000E-01,
                 A3  = -1.4419555664063E-01,
                 A4  = -2.775764465332E-01,
                 A5  = -6.7659258842468E-01,
                 A6  = -1.9935317337513E+00,
                 A7  = -6.8839142681099E+00,
                 A8  = -2.7248827311269E+01,
                 A9  = -1.2159789187654E+02,
                 A10 = -6.0384407670507E+02,
                 A11 = -3.3022722944809E+03;

  G4double I = 0.0;
  if (x == 0.0)
  {
    I = 0.0;
  }
  else if (x < 18.0)
  {
    I          = 1.0;
    G4double y = x * x;
    G4double q = 1.0;
    for (G4int i=1; i<101; i++)
    {
      q *= 0.25 * y / i / (i+1.0);
      I += q;
      if (std::abs(q/I) < 1.0E-15) break;
    }
    I *= 0.5 * x;
    
  }
  else
  {
    G4double y = 1.0 / x;
    I = G4Exp(x) / std::sqrt(twopi*x) *
      (1.0 + y*(A0+y*(A1+y*(A2+y*(A3+y*(A4+y*(A5+y*(A6+y*(A7+y*(A8+y*(A9+y*(A10+y*A11))))))))))));
  }

  return I;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Bessel::pK0

(

G4double

x

)

Definition at line 310 of file G4Bessel.cc.

{
  const G4double A0 = 0.1250000000000E+00,
                 A1 = 0.2109375000000E+00,
                 A2 = 1.0986328125000E+00,
                 A3 = 1.1775970458984E+01,
                 A4 = 2.1461706161499E+02,
                 A5 = 5.9511522710323E+03,
                 A6 = 2.3347645606175E+05,
                 A7 = 1.2312234987631E+07;

  G4double K = 0.0;
  if (x == 0.0)
  {
    K = 1.0E+307;
  }
  else if (x < 9.0)
  {
    G4double y = x * x;
    G4double C = -G4Log(x/2.0) - 0.5772156649015329;
    G4double q = 1.0;
    G4double t = 0.0;
    for (G4int i=1; i<51; i++)
    {
      q *= 0.25 * y / i / i;
      t += 1.0 / i ;
      K += q * (t+C);
    }
    K += C;
  }
  else
  {
    G4double y = 1.0 / x / x;
    K = 0.5 / x / pI0(x) *
      (1.0 + y*(A0+y*(A1+y*(A2+y*(A3+y*(A4+y*(A5+y*(A6+y*A7))))))));
  }
  
  return K;
}

Here is the call graph for this function:

Here is the caller graph for this function:

G4double G4Bessel::pK1

(

G4double

x

)

Definition at line 351 of file G4Bessel.cc.

{
  G4double K = 0.0;
  if (x == 0.0)
    K = 1.0E+307;
  else
    K = (1.0/x - pI1(x)*pK0(x)) / pI0(x);
  return K;
}

Here is the call graph for this function:

---

The documentation for this class was generated from the following files:

• geant4.10.03.p01/source/processes/hadronic/util/include/G4Bessel.hh
• geant4.10.03.p01/source/processes/hadronic/util/src/G4Bessel.cc